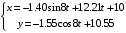ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 26
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическое задание 7
Тема 3.1. Динамика материальной точки
Задание
Материальная точка массой Г + 1 (кг) движется в горизонтальной плоскости ХОY системы координат под действием силы F̅, где ее проекция на ось Х равна (C + 800)sin(Гt) (Н), а на ось Y равна (900 – П)cos(Гt) (Н). Определите уравнение движения точки при следующих начальных условиях: начальная абсцисса равна П + 2 (м); начальная ордината равна Г + 1 (м); проекция вектора начальной скорости на ось Х равна С – 6 (м/с); проекция вектора начальной скорости на ось Y равна 0 (м/с).
Рекомендации по выполнению задания 7
-
Выделите материальную точку, движение которой рассматривается. -
Расставьте внешние силы, действующие на материальную точку. -
Выделите тела связей с их реакциями. -
Постройте систему координат. -
Составьте дифференциальные уравнения абсолютного движения материальной точки. -
Решите дифференциальные уравнения абсолютного движения материальной точки.
Бланк выполнения задания 7
1. Записываются данные задания.
Материальная точка массой 9 (кг) движется в горизонтальной плоскости ХОY системы координат под действием силы F̅, где ее проекция на ось Х равна (807)sin(Гt) (Н), а на ось Y равна (892)cos(Гt) (Н). Определите уравнение движения точки при следующих начальных условиях: начальная абсцисса равна 10 (м); начальная ордината равна 9 (м); проекция вектора начальной скорости на ось Х равна 1 (м/с); проекция вектора начальной скорости на ось Y равна 0 (м/с).
2. Представляется рисунок, на котором показаны все силы.
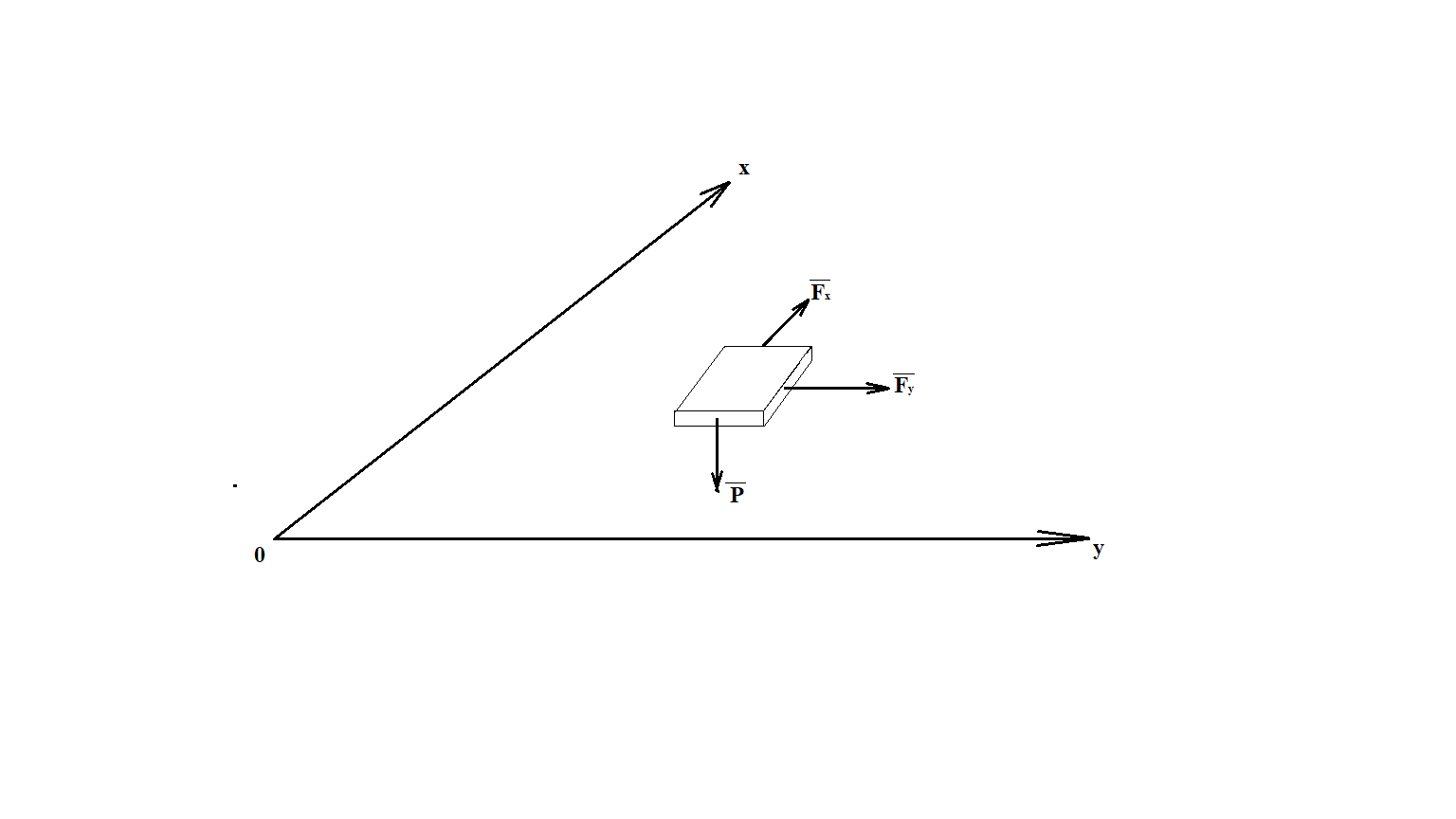
3. Записываются уравнения динамики материальной точки.
Рассмотрим движение точки в плоскости ХОУ. Изображаем материальную точку и действующие на нее силы
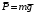 ,F. Проводим оси ОХ, ОУ.
,F. Проводим оси ОХ, ОУ.Составляем дифференциальные уравнения движения груза в плоскости на эти оси.
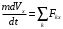 ;
; 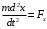 ;
; 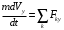 ;
; 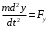 (1)
(1)где
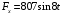
;
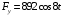
;
4. Решаются уравнения динамики материальной точки.
Разделяя в уравнении (1) переменные, а затем взяв от обеих частей интегралы, получим:
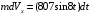 ;
; 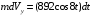
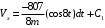 ;
; 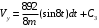
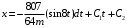 ;
;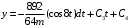
начальные условия при t=0
x0=10м; y0=9м; Vx0=1 м/c; Vy0=0 м/c;
тогда:
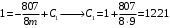 ;
;С2=10; С3=0;
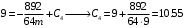
5. Записывается ответ.
Уравнения движения примут вид: