Файл: Реферат по дисциплине Математическое обеспечение финансовых решений.docx
Добавлен: 26.10.2023
Просмотров: 42
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
n
E = S Xi * Ei
i =1
Для дисперсии эта сумма применима с определенными ограничениями, так как изменение курса акций на рынке происходит не изолировано друг от друга, а охватывает весь рынок в целом. Поэтому дисперсия зависит не только от степени рассеивания отдельных ценных бумаг, а также от того, как все ценные бумаги в совокупности одновременно понижаются или повышаются по курсу, т.е. от корреляции между изменениями курсов отдельных ценных бумаг. Итак, Марковитц разработал очень важное для современной теории портфеля ценных бумаг положение, которое гласит: совокупный риск портфеля можно разложить на две составные части. С одной стороны, это так называемый систематический риск, который нельзя исключить и которому подвержены все ценные бумаги практически в равной степени. С другой – специфический риск для каждой конкретной ценной бумаги, который можно избежать при помощи управления портфелем ценных бумаг.
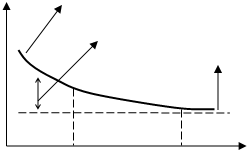
Рис.1.1. Возможность уменьшения риска при помощи управления портфелем ценных бумаг.
При этом сумма сложенных средств по всем объектам должна быть равна общему объему инвестиционных вложений (например, часть средств на банковском счете вводится в модель как инвестиция с нулевым риском), т.е. сумма относительных долей Xj в общем объеме должна равняться единице:
n
S Xi = 1
i =1
Проблема заключается в численном определении относительных долей акций и облигаций в портфеле (значений Xj ), которые наиболее выгодны для владельца. Марковитц ограничивает решение модели тем, что из всего множества “допустимых портфелей”, т.е. удовлетворяющих ограничениям, необходимо выделить те, которые рискованнее, чем другие. Это портфели, содержащие при одинаковом доходе больший риск (дисперсию) по сравнению с другими, или портфели, приносящие меньший доход при одинаковом уровне риска. При помощи разработанного Марковитцем метода критических линий можно выделить неперспективные портфели, не удовлетворяющие ограничениям. Тем самым остаются только эффективные портфели, т.е. портфели, содержащие минимальный риск при заданном доходе или приносящие максимально возможный доход при заданном максимальном уровне риска, на который может пойти инвестор. Данный факт имеет большое значение в современной теории портфелей ценных бумаг. Отобранные таким образом портфели объединяют в список, содержащий сведения о процентном составе портфеля из отдельных ценных бумаг, а также о доходе и риске портфелей. Выбор конкретного портфеля зависит от максимального риска, на который готов пойти инвестор. На рис. 1.2 представлены недопустимые, допустимые и эффективные портфели. Портфель является эффективным, если он удовлетворяет ограничениям, и, кроме того, для заданного дохода, например Е1 , содержит меньший риск R1 по сравнению с другими портфелями, приносящими такой же доход Е1 , или при определенном риске R2 приносит более высокий доход Е2 по сравнению с другими комбинациями с R2 .
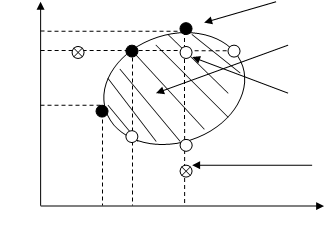
Рис. 1.2. Недопустимые, допустимые и эффективные портфели
Разделение риска на независимые составляющие дает любому инвестору возможность проанализировать ценные бумаги со всех сторон и определить их сильные и слабые стороны при формировании портфеля. С методологической точки зрения модель Марковица можно определить как практически-нормативную, что, конечно, не означает навязывания инвестору определенного стиля поведения на рынке ценных бумаг. Задача модели заключается в том, чтобы показать, как поставленные цели достижимы на практике. Отрицательной чертой модели Марковица можно назвать то, что для решения задачи Г. Марковица требуется большой объем данных о рынке ценных бумаг, накопленных за многие годы и отвечающих условиям представительности. На практике, особенно на российском фондовом рынке, который лишь недавно был сформирован, такие данные получить очень трудно, а подчас и невозможно.
ПРОБЛЕМЫ, ВОЗНИКАЮЩИЕ ПРИ ИСПОЛЬЗОВАНИИ «ОПТИМИЗАТОРОВ»
Предположим, что капитан современного комфортабельного лайнера принимает решение не использовать современную навигационную систему (систему, которая с помощью компьютеров и спутников определяет местоположение корабля с точностью до нескольких футов). Вместо этого он собирается положиться на метод навигации по звездам - старинный метод, имеющий проблемы и приводящий к неточностям. Большинство людей будут считать выбор капитана в лучшем случае эксцентричным, в худшем - чрезвычайно опасным. Когда дело касается формирования портфелей, большинство менеджеров по инвестициям делают свой выбор аналогично капитану данного судна. Они отрицают методы формирования портфелей, основанные на использовании компьютеров, и используют традиционные подходы. Являются ли их решения настолько же глупыми, как и решения капитана корабля? Или, может быть, данный подход продиктован их очевидным сумасшествием?
Концепция эффективного множества и оптимального портфеля инвестора являются основополагающими в современной инвестиционной теории. В начале 50-х годов Гарри Марковиц описал решение данных проблем. Используя математический метод известный как квадратичное программирование инвестор может обработать ожидаемые доходности, стандартные отклонения и ковариации для определения эффективного множества. Имея оценку своих кривых безразличия, отражающую их индивидуальный допустимый риск, он может затем выбрать портфель из эффективного множества. С появлением дешевых и высокопроизводительных компьютеров в 80-х годах, а также с развитием сложных моделей риска стало возможным определение эффективного множества для нескольких тысяч ценных бумаг за несколько минут. Необходимое компьютерное оборудование и программное обеспечение являются доступными фактически для любого инвестиционного института. В действительности данный процесс стал настолько банальным, что даже приобрел собственную терминологию. Использование компьютера для определения эффективного множества и формирования оптимального портфеля в разговорном языке называется оптимизацией. Портфели «оптимизируются», а про инвесторов говорят, что они применяют оптимизационную технику. Несмотря на доступность «оптимизаторов», относительно небольшое число менеджеров по инвестициям в действительности используют их при формировании портфеля. Вместо этого они в основном полагаются на некоторый набор правил и закономерностей.
Почему менеджеры по инвестициям отказываются применять оптимизационную технику при формировании портфелей? Причиной сопротивления являются два момента: профессиональные интересы и несоответствия в практическом воплощении концепций. С точки зрения профессиональных факторов большинство инвесторов просто не чувствуют себя комфортно при использовании качественных методов. В их методах принятия решений подчеркивается значение интуиции и субъективных решений. Использование оптимизационной техники в формировании портфеля требует наличия системной и формальной структуры принятия решений. Специалисты по анализу ценных бумаг должны принять на себя ответственность за формирование количественных прогнозов ожидаемой доходности и риска. Управляющие портфелями должны выполнять решения компьютера. В результате этого «оптимизаторы» уничтожают «артистизм и грацию» управления инвестициями.
Кроме того, с внедрением «оптимизаторов» возрастает влияние новой породы профессионалов по инвестициям — числовых аналитиков (презрительно именуемых «квантами»), которые координируют получение и применение оценок риска и доходности. Авторитет, приобретаемый числовыми аналитиками, уменьшает влияние аналитиков и менеджеров портфелей, использующих традиционные методы, к их большому неудовольствию. Что касается перспектив применения «оптимизаторов», то здесь существуют серьезные проблемы. В частности, они имеют тенденцию к созданию чисто интуитивных портфелей, не подходящих для реальных инвестиций. Данная ситуация объясняется не столько проблемами «оптимизаторов», сколько ошибками операторов, обеспечивающих ввод данных. Здесь работает парадигма GIGO. (что расшифровывается как «мусор на входе - мусор на выходе»).
«Оптимизаторы» предпочитают ценные бумаги, обладающие высокими ожидаемыми доходностями, малыми стандартными отклонениями и малой величиной ковариации с другими ценными бумагами. Очень часто при оценке этих величин используется информация из старых баз данных, содержащих тысячи ценных бумаг. До тех пор пока информация о доходности и риске не будет тщательно проверена, ошибки (например, преуменьшение стандартного отклонения ценных бумаг) могут привести к тому, что «оптимизатор» будет рекомендовать произвести покупку некоторых ценных бумаг, исходя из неправильных предпосылок. Даже если информация является выверенной, экстремальные исторические события могут привести «оптимизатор» к практически неверным решениям. До тех пор пока программа не будет принимать во внимание операционные издержки «оптимизаторы» будут также демонстрировать плохую привычку к операциям, приводящим к большому обороту, и рекомендациям о покупке ценных бумаг низкой ликвидностью. Высокий оборот связан с существенными изменениями в портфеле от периода к периоду. Высокий оборот может являться причиной неприемлемо высок их операционных издержек, отрицательно сказывающихся на функционировании данного портфеля. Ликвидность (liquidity) означает возможность реального приобретения ценных бумаг, выбранных «оптимизатором». Выбранные бумаги могут обладать желательными характеристиками по доходности и риску, но продаваться в незначительных количествах, не позволяющих институциональным инвесторам приобрести их без ощутимых дополнительных расходов на покупку. Существуют различные решения данных проблем, начиная с аккуратной проверки вводимой информации и кончая введением ограничений; на максимальный Оборот и минимальную ликвидность. Тем не менее, ничто не может заменить прогноз квалифицированного специалиста о доходности и риске ценных бумаг, основанный на правильном применении понятия рыночного равновесия. Профессиональные проблемы и проблемы практического воплощения дают менеджерам по инвестициям удобный повод избегать применения «оптимизаторов» и сконцентрироваться на использовании традиционных методов формирования портфелей. Однако рассмотрение количественных методов формирования портфелей очень важно. Повышающаяся эффективность финансовых рынков заставляет менеджеров институциональных инвесторов обрабатывать больше информации о большем количестве ценных бумаг и с большей скоростью, чем когда-либо раньше. Как следствие, они вынуждены в большей степени увеличить использование количественных инструментов анализа инвестиций. Хотя большинство из них еще не включили «оптимизаторы» в процедуру формирования портфелей, фактически все они стали более восприимчивы к необходимости создания диверсифицированных портфелей, имеющих наивысший уровень ожидаемой доходности при удовлетворительном уровне риска.
Прикладной смысл оптимального портфеля и границы эффективности. Прикладной смысл модели оптимального портфеля очень прост и в то же время полезен: зная вашу ожидаемую норму доходности, вы можете вычислить справедливый процент риска. И наоборот: зная риск, который вы готовы терпеть, вы можете вычислить справедливую норму доходности для этого риска. Но сами не пытайтесь делать эти вычисления в уме. Делать соответствующие просчеты вам помогут сотрудники финансовой компании, т.к. для этого необходимо специальное программное обеспечение.
ЗАКЛЮЧЕНИЕ
При самоличном составлении портфеля или при следующем общении с менеджером портфелей в ИСИ (ПИФ) задайте себе (или менеджеру) вопрос: «оптимален ли мой инвестиционный портфель и находится ли он на границе эффективности Марковица?» Если нет, то обязательно поместите ваш портфель на границу эффективности, а то он будет продолжать быть неоптимальным и приносить вам заниженную прибыль. Также любые модели инвестиционного портфеля являются открытыми системами и соответственно могут дополняться и корректироваться при изменениях условий на финансовом рынке. Модель инвестиционного портфеля позволяет получить аналитический материал, необходимый для принятия оптимального решения в процессе инвестиционной деятельности. Определив для себя структуру портфеля, инвестор занимает по отношению к рынку как бы статическую позицию и может сохранять ее достаточно долго, если сам рынок сохраняет общую динамику и внутренние пропорции. Вместе с тем при резких изменениях в рыночной ситуации или неожиданных сдвигах в доходах и курсах конкретных бумаг, инвестор может срочно откорректировать свой портфель с помощью широчайшего арсенала способов, в том числе предоставляемых опционными сделками и их сочетаниями с короткими и длинными позициями по отдельным бумагам. еория формирования инвестиционного портфеля, предложенная нобелевским лауреатом по экономике Гарри Марковицем, является наиболее распространенной и популярной. Суть теории Марковица заключается в том, что диверсификация всегда дает инвестору преимущество (ученый это математически доказал). Кроме того, Марковиц выдвинул следующий тезис: риск инвестиционного портфеля зависит не только от того, какую долю занимает определенный актив, но и от взаимосвязей, существующих между всеми активами, входящими в портфель. Оптимален тот портфель, который включает в себя акции компаний, занимающихся разными видами деятельности, относящихся к разным отраслям и минимально между собой коррелирующих. Если есть возможность, лучше собрать портфель из разнородных инструментов: акций, облигаций, валютных пар. В дополнение, ранее было доказано, что максимальное количество активов, которые могут быть включены в один портфель – 20. Если активов больше, эффективность портфеля уже не будет максимальной.
СПИСОК ЛИТЕРАТУРЫ
-
Буренин А.Н. Управление портфелем ценных бумаг./ А.Н. Буренин - М.: Научно-техническое общество имени академика С.И. Вавилова, 2008. - 81 с. -
А.А. Шабалин “Построение оптимального портфеля из некоторых российских ценных бумаг с помощью моделей математической оптимизации” -
Инвестиции: Учебник для вузов. / В. Бочаров - СПб: Питер, 2007. -
Шарп У., Александер Г., Бейли Дж. Инвестиции. - М.: Инфра-М, - 2006 -
Буренин А.Н. Управление портфелем ценных бумаг М., Научно-техническое общество имени академика СИ. Вавилова, 2008, - 440 с. -
Шапкин, А.С. Управление портфелем инвестиций ценных бумаг: учебник / А.С. Шапкин. - М.: Дашков и К, 2006. - 91 с. -
Алиев А.Т. Управление инвестиционным портфелем: учебное пособие / А.Т. Алиев, К.В. Сомик. - М.: Дашков и Ко, 2015. - 159 с. - ISBN 978-5-394-01292-1; То же [Электронный ресурс]. - URL: https://biblioclub.ruгл.1 п.1.3. -
Брюков В.Г. Управление портфелями акций в условиях подъема/ В.Г. Брюков // Инвестиционный банкинг. - 2009. - №2. - С. 22-29. -
Рухлов А. Принципы портфельного инвестирования. – Финансы. Ценные бумаги. – 2005 -
Хабров В.В. Оптимизация управления инвестиционным портфелем на основе моделей векторных авторегрессий и моделей многомерной волатильности / В.В. Хабров // Прикладная эконометрика. – 2012. – № 4. – С. 35-62. -
Дудов С. И. Оптимальное портфельное инвестирование // Учебное пособие для студентов экон.-мат. специальностей/ С.И. Дудов. – 2008. – С. 59. -
Скрипниченко М.В.Портфельные инвестиции: Учебное пособие. - СПб: Университет ИТМО, 2016 - 40с.
Смоленск – 2022