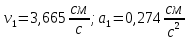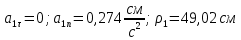ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 16
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования
«Тольяттинский государственный университет»
Институт инженерной и экологической безопасности
| (наименование института полностью) |
| 20.03.01 Техносферная безопасность |
| (код и наименование направления подготовки / специальности) |
| Противопожарные системы |
| (направленность (профиль) / специализация) |
ПрактическОе заданиЕ 4
по учебному курсу «Механика»
| Обучающегося | | |
| | (И.О. Фамилия) | |
| Группа | | |
| | | |
| Преподаватель | | |
| | (И.О. Фамилия) | |
Тольятти 2023
Задание 4
Дано:
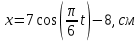
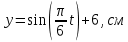
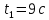
Найти: 1) Уравнение траектории точки
2)
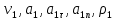в момент времени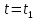 
Решение
Для определения уравнения траектории точки исключим из заданных уравнений время
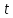. Из первого уравнения выразим 
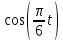и возведём обе части полученного уравнения в квадрат: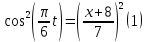
Из первого уравнения выразим
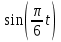и возведём в квадрат: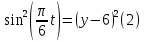
Складывая уравнения (1) и (2) с учётом тригонометрического тождества
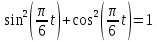получим уравнение траектории точки: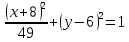
Это уравнение эллипса с центром в точке (–8; 6) и полуосями
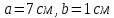(рис. 1).
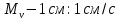
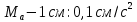
12
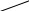
8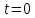 
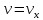
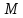
4
-16 -12 -8 -4 0
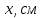
Рис. 1
Вычисляем координаты точки в начальный момент времени
:
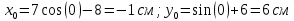
Вычисляем координаты точки в заданный момент времени
:
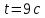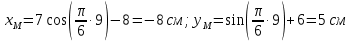
Изображаем точку в этом положении (точка
на рис. 1).Скорость точки находим по проекциям на координатные оси:
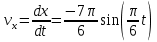
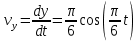
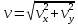
В момент времени
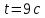получаем: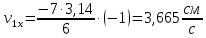
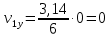
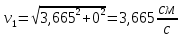
Аналогично определяем ускорение точки:
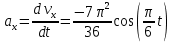
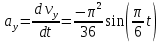
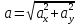
В момент времени
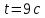получаем: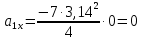
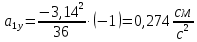
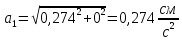
Касательное ускорение определяем по формуле:
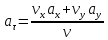
В момент времени
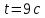получаем: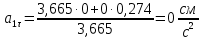
Нормальное ускорение и радиус кривизны траектории находим по формулам:
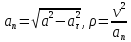
В момент времени
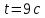получаем: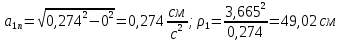
Векторы скорости и ускорения в выбранных масштабах построены на рис. 1.
Ответ:
