Файл: Исследование рычажного механизма 5 2 Кинетостатический (силовой) анализ рычажного механизма 16.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 104
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
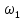 – угловая скорость звена 1, рад/с;
– угловая скорость звена 1, рад/с;Угловую скорость звена 1 можно найти по следующей формуле:
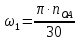 , , | (1.7) |
где
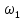 – угловая скорость звена 1, рад/с;
– угловая скорость звена 1, рад/с; – частота вращения кривошипа ОА, об/мин.
– частота вращения кривошипа ОА, об/мин.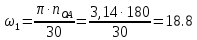 .
.Тогда
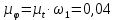 .
.Дифференцируя график перемещений, получим график изменения скорости ведомого звена. Дифференцирование проводим графически методом хорд.
Вычисляем масштабный коэффициент скорости на диаграмме
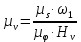 , , | (1.8) |
где
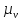 – масштабный коэффициент скорости на диаграмме, м · с-1/мм;
– масштабный коэффициент скорости на диаграмме, м · с-1/мм;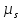 –масштабный коэффициент перемещений на диаграмме, м/мм;
–масштабный коэффициент перемещений на диаграмме, м/мм;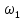 – угловая скорость звена 1, рад/с;
– угловая скорость звена 1, рад/с; – масштабный коэффициент угла поворота кривошипа, рад/мм;
– масштабный коэффициент угла поворота кривошипа, рад/мм;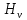 –полюсное расстояние, мм.
–полюсное расстояние, мм.Полюсное расстояние
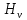 принимают равным 15 мм.
принимают равным 15 мм.Тогда
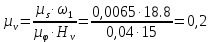 .
.Аналогичным способом получим кривую ускорения, дифференцируя график скорости.
Вычисляем масштабный коэффициент ускорения на диаграмме
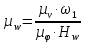 , , | (1.9) |
где
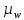 – масштабный коэффициент ускорения на диаграмме, м · с-2/мм;
– масштабный коэффициент ускорения на диаграмме, м · с-2/мм;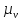
– масштабный коэффициент скорости на диаграмме, м · с-1/мм;
 – угловая скорость звена 1, рад/с;
– угловая скорость звена 1, рад/с; – масштабный коэффициент угла поворота кривошипа, рад/мм;
– масштабный коэффициент угла поворота кривошипа, рад/мм;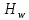 –полюсное расстояние, мм.
–полюсное расстояние, мм.Полюсное расстояние
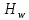 принимают равным 15 мм.
принимают равным 15 мм.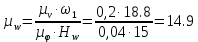 .
.1.5. Описание построения плана скоростей
От произвольно взятой точки Р отложим вектор скорости
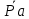 , который направлен перпендикулярно кривошипу в направлении
, который направлен перпендикулярно кривошипу в направлении .Принимаем длину вектора Ра на плане скоростей равной 40 мм.
.Принимаем длину вектора Ра на плане скоростей равной 40 мм.Вращение кривошипа задано схемой механизма и направлено против часовой стрелки.
Скорость точки B кривошипа можно найти, предварительно рассчитав угловую скорость вращения кривошипа:
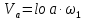 , , | (1.10) |
где
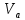 – скорость точки A кривошипа, м/с;
– скорость точки A кривошипа, м/с; – угловая скорость звена 1, рад/с;
– угловая скорость звена 1, рад/с;lОА– длина кривошипа по заданию, м.
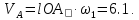
Расчет масштабного коэффициента скорости
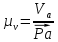 , , | (1.11) |
где
 – масштабный коэффициент скорости,м · с-1/мм;
– масштабный коэффициент скорости,м · с-1/мм;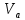 – скорость точки А кривошипа, м/с;
– скорость точки А кривошипа, м/с;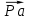 – длина вектора
– длина вектора 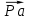 на плане скоростей, мм.
на плане скоростей, мм.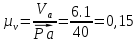 .
.Для каждого из 12 положений:
Скорость точки В ползуна найдем, решив совместно два векторных уравнения
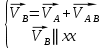 . . | (1.12) |
Первое уравнение описывает движение точки В относительно точки А, а второе описывает движение точки В, принадлежащей ползуну.
Скорость точки С определим по теореме подобия:
АВ/АС=(аb)/(ac)
Следовательно:
ac=AC x ab/AB=24 x 19/185=4 мм
Тогда:
Vc=Pc x Mv=44x0.15=6.6 м/с
Скорость точки D ползуна найдем, решив совместно два векторных уравнения
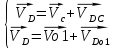 . . | (1.13) |
Первое уравнение описывает движение точкиD относительно точки C, а второе описывает движение точкиD,относительно О1.
Векторы скоростей
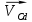 строим из точки C перпендикулярно шатунам 4.
строим из точки C перпендикулярно шатунам 4.После построения плана скоростей определяем значения скоростей всех звеньев и точек механизма.:
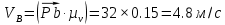
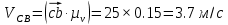
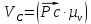 =44х0.15=6.6м/с
=44х0.15=6.6м/с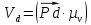 =3х0.15=0.45м/с
=3х0.15=0.45м/с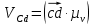 =39х0.15=5.8м/с
=39х0.15=5.8м/с1.6. Описание построения плана ускорений
От полюса π отложим вектор нормального ускорения в направлении от А к О в виде вектора
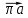 .
.Нормальное (центростремительное) ускорение точки В кривошипа найдем по формуле
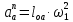 , , | (1.14) |
где
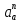 – нормальное ускорение точки В, м/с2;
– нормальное ускорение точки В, м/с2; – угловая скорость звена 1, рад/с;
– угловая скорость звена 1, рад/с;Lоа– длина кривошипа по заданию, м.
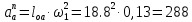
Принимаем длину вектора
 .
.Расчет масштабного коэффициента ускорения проведем по формуле
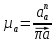 , , | (1.15) |
где
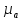 – масштабный коэффициент ускорения,м · с-2/мм;
– масштабный коэффициент ускорения,м · с-2/мм;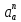 – нормальное ускорение точки В, м/с2;
– нормальное ускорение точки В, м/с2;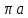 – длина вектора
– длина вектора 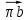 на плане скоростей, мм.
на плане скоростей, мм.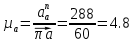 .
.Для каждого из 2 положений:
Ускорение точки C найдем, решив совместно два векторных уравнения
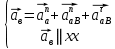 . . | (1.16) |
Скорость точки С определим по теореме подобия:
АВ/АС=(аb)/(ac)
Следовательно:
ac=AC x ab/AB=24 x 52/185=7 мм
Тогда:
Vc=Pc x Mv=44x0.15=6.6 м/с
Ускорение точки D найдем, решив совместно два векторных уравнения
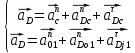 . . | (1.17) |
Нормальные ускорения
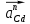 и
и 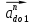 строим параллельно шатунам 3 и кулисе 4 соответственно, причем они направлены от точекС и D .
строим параллельно шатунам 3 и кулисе 4 соответственно, причем они направлены от точекС и D .Тангенциальные ускорения
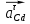 и
и 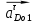 строим перпендикулярно нормальным ускорениям
строим перпендикулярно нормальным ускорениям 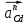 и
и 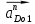 из конца векторов до пересечения.
из конца векторов до пересечения.
Для 0-го положения:
Нормальное ускорение
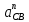 определим по формуле
определим по формуле 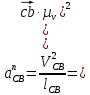 , , | (1.18) |
где
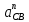 – нормальное ускорение звена CB, м/с2;
– нормальное ускорение звена CB, м/с2;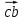 – длина вектора
– длина вектора 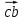 скорости шатуна СВ на чертеже, мм;
скорости шатуна СВ на чертеже, мм;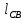 – действительная длина шатуна CB, м.
– действительная длина шатуна CB, м.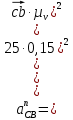 .
.На плане ускорений длина вектора
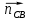 будет равна
будет равна 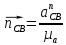 , , | (1.19) |
где
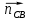 – длина вектора нормального ускорения точки B кривошипа, мм;
– длина вектора нормального ускорения точки B кривошипа, мм;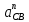 – нормальное ускорение звена CB, м/с2;
– нормальное ускорение звена CB, м/с2; – масштабный коэффициент ускорения,м · с-2/мм.
– масштабный коэффициент ускорения,м · с-2/мм.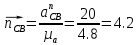 .
.Нормальное ускорение
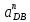 найдем по формуле (1.18)
найдем по формуле (1.18)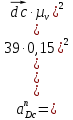
А длину вектора
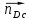 по формуле (1.19)
по формуле (1.19)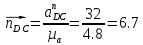 .
.Сравнительный анализ
Рассчитаем скорость и ускорение выходного звена, полученные построением планов скоростей. Для этого умножаем длину вектора абсолютной скорости ползуна В на масштабный коэффициент плана скоростей и длину вектора абсолютного ускорения на масштабный коэффициент плана ускорений.
| План скоростей 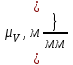 | 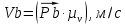 |
| План ускорений 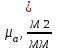 | 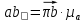 , м/с2 , м/с2 |