ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 11
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Виды множеств в зависимости от количества элементов
Основной характеристикой множеств является количество элементов, содержащихся в этом множестве.
По данному признаку выделяются:
1. Множество, содержащее конечное число элементов называется конечным.
Количество элементов конечного множества называют его мощностью.
2. Множество, не являющееся конечным, называется бесконечным.
3. Если множество не содержит элементов, то оно называется пустым и обозначается
.
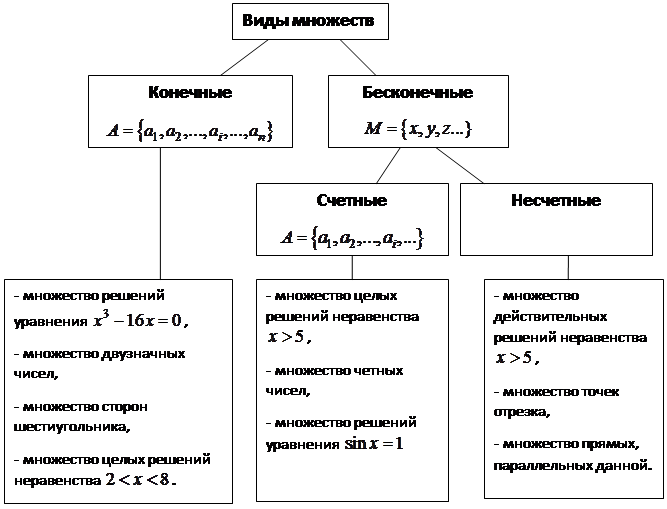
1. Конечное множество по признаку мощности характеризуется:
Два множества А и В называются эквивалентными, или, равномощными, если между их элементами можно установить взаимно-однозначное соответствие.
Пример: Рассмотрим множества, состоящие из букв слов:
; 
; 
; 
.Множества А, В и С имеют равные мощности:
, а мощность множества D меньше 
.При этом, множества А и В равны, а множества А и С – эквивалентны.
Эталоном для сравнения множеств служит натуральный ряд чисел. Поэтому все числовые последовательности
, содержащие различные элементы, эквивалентны натуральному ряду чисел, что видно по их индексам.
2. Бесконечное множество, которое эквивалентно множеству натуральных чисел, называется счетным.
Говорим, что все элементы счетного множества пронумерованы.
В противном случае бесконечное множество будет несчетным.
В 1878 году Георг Кантор доказал, что множество точек, расположенных на отрезке от 0 до 1 несчетно.
Во множестве могут быть выделеныподмножества.
Если каждый элемент множества K принадлежит множеству М, то множество К называют подмножеством множества М и обозначают
.Например:
1) множество всех книг данного автора в библиотеке, есть подмножество всех книг в библиотеке.
2) множество студентов, обучающихся на "4" и "5" в группе есть подмножество всех студентов группы.
3)
четных чисел меньших или равных 6, есть подмножество множества 
.Пустое множество является подмножеством любого множества.
Количество подмножеств для исходного множества может быть рассчитано.
Для этого познакомимся с термином булеан.
Булеаном множества М (N(M)) называется множество всех его подмножеств.
Пример:
Рассмотрим множество
. Составим все подмножества множества М.
,
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
.Подмножества
и 
являются несобственными подмножествами множества М,остальные – 2-15 – это собственные подмножества.
Всего мы нашли 16 различных подмножеств множества М. Это число 16 может выразить:
.В общем случае, для любого конечног о множества, состоящего из n элементов, число возможных подмножеств равно
.Множество U,
состоящее из всех возможных элементов, обладающих данным признаком, называется универсальным.
. Принадлежность элементов множеству обозначается знаком – Є. Пример: N = {a, b, c, y}, а Є N – элемент «а» принадлежит N.