Файл: Задача Расчёт разветвленной линей ной цепи постоянного тока с несколькими источниками электрической энергии.docx
Добавлен: 26.10.2023
Просмотров: 275
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача № 1. Расчёт разветвленной линейной цепи постоянного тока с несколькими источниками электрической энергии
Для электрической цепи известны ЭДС E1, E2 источников питания, а
также сопротивления R1 - R6. Необходимо:
1. Составить систему уравнений для определения токов путем
непосредственного применения законов Кирхгофа. Решать эту систему
уравнений не следует.
2. Определить токи ветвей методом контурных токов.
3. Составить баланс мощностей. Значения параметров элементов цепи
приведены в таблицу 1.
Таблица 1
| Вариант |  |  |  |  |  |  |  |  |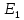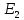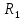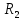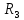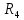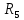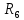
| В | Ом | |||||||
| 7 | 135 | 75 | 7 | 4 | 7 | 2 | 5 | 8 |
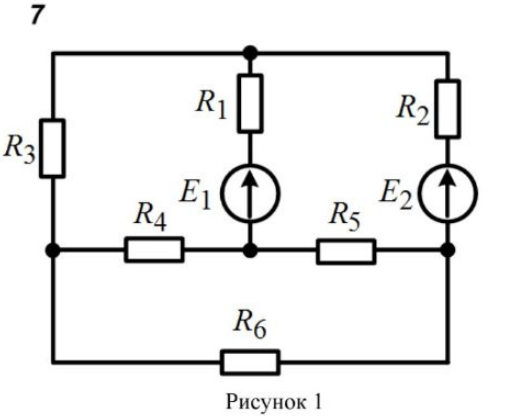
Рисунок 1
Решение
1.Произвольно расставим направления токов в ветвях цепи, примем
направления обхода контуров, обозначим узлы.
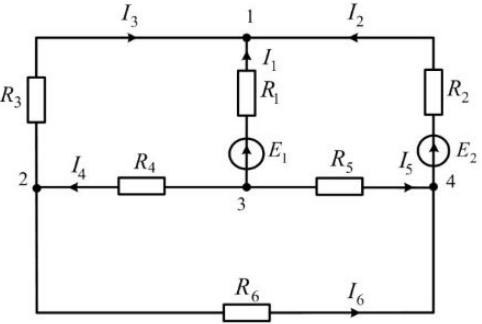
Рисунок 2
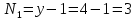
y-количество узлов
Составим 3 уравнение по первому закону Кирхгофа.
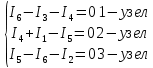
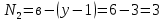
в – количество ветвей
По второму закону Кирхгофа составим 3 уравнения
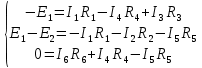
Токи и напряжения, совпадающие с принятым направлением обхода с
«+», несовпадающие с «-».
2.Определим токи во всех ветвях методом контурных токов. Зададимся
направлениями течения контурных токов в каждом контуре схемы и обозначим
их
.
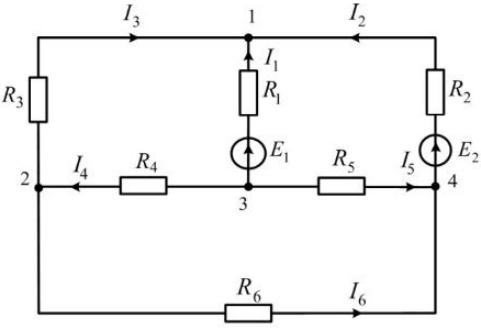
Рисунок 3д
Определим контурные сопротивления
,
,
=
,
=
,
=
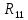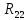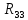
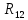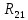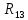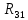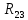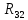- взаимное сопротивление контуров
,
,
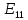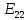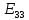- контурный ЭДС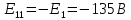
=
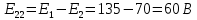
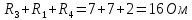
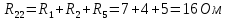
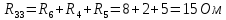
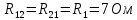
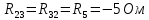
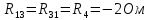
Составим систему уравнений для контуров нашей цепи.
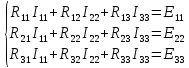
Подставим числовые значения и решим.
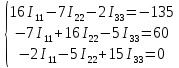
Решение
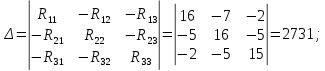
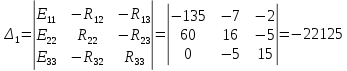
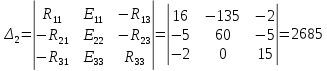
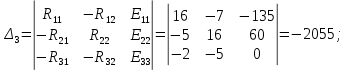
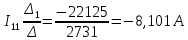
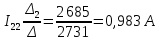
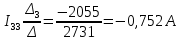
Определим фактические токи в ветвях цепи:
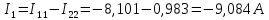
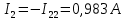
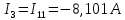
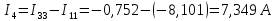
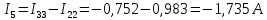
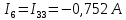
3. Составим баланс мощностей
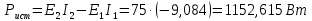
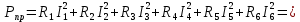
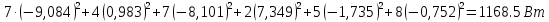
Задача № 2. Расчёт разветвленной цепи однофазного синусоидального тока
Электрическая цепь (рисунок 4), подключенная к сети переменного тока с напряжением U и частотой 50 Гц, имеет параметры, численные значения которых приведены в таблице 2.
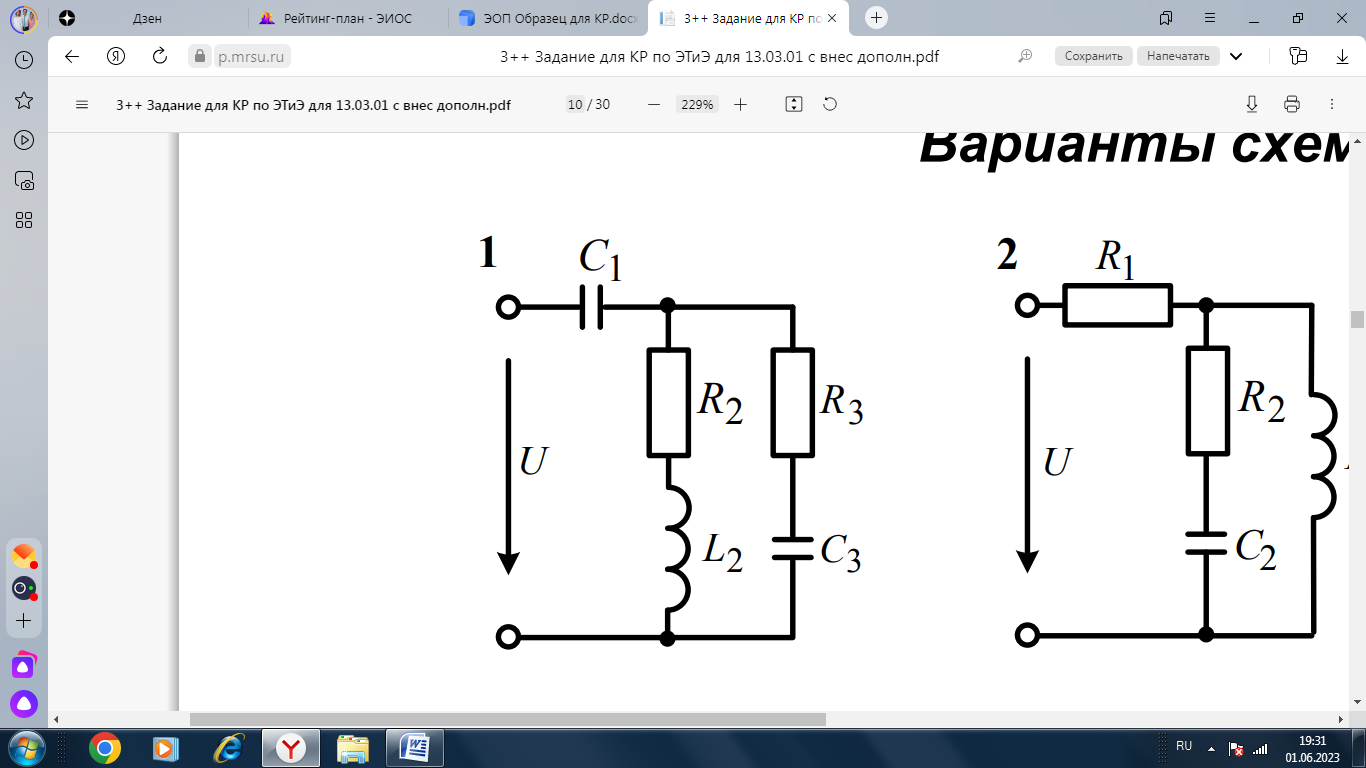
Рисунок 4
Таблица 2
| Вари- ант | U , В | R1 , Ом | L1 , мГн | С1 , мкФ | R2 , Ом | L2 , мГн | С2 , мкФ | R3 , Ом | L3 , мГн | С3 , мкФ |
| 6 | 220 | 4 | 14 | 1000 | 12 | 31 | 700 | 5 | 13 | 460 |
Необходимо:
1. Рассчитать сопротивления реактивных элементов цепи;
2.Определить действующие значения токов в ветвях с помощью комплексных чисел;
3. По полученным комплексным изображениям записать выражения для мгновенных значений напряжения на разветвлѐнном участке цепи и токов в ветвях;
4. Составить баланс активных и реактивных мощностей;
5. Построить векторную диаграмму, на которой изобразить векторы всех токов и напряжений на участках цепи.
Примечание. Для всех вариантов принять u 0
Решение
1. Вычислим сопротивления реактивных элементов цепи:
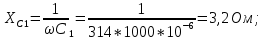
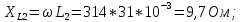
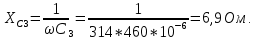
Определим комплексные сопротивления отдельных ветвей цепи:
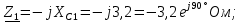
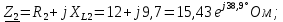
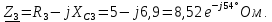
Преобразованная цепь представлена на рисунке 5:
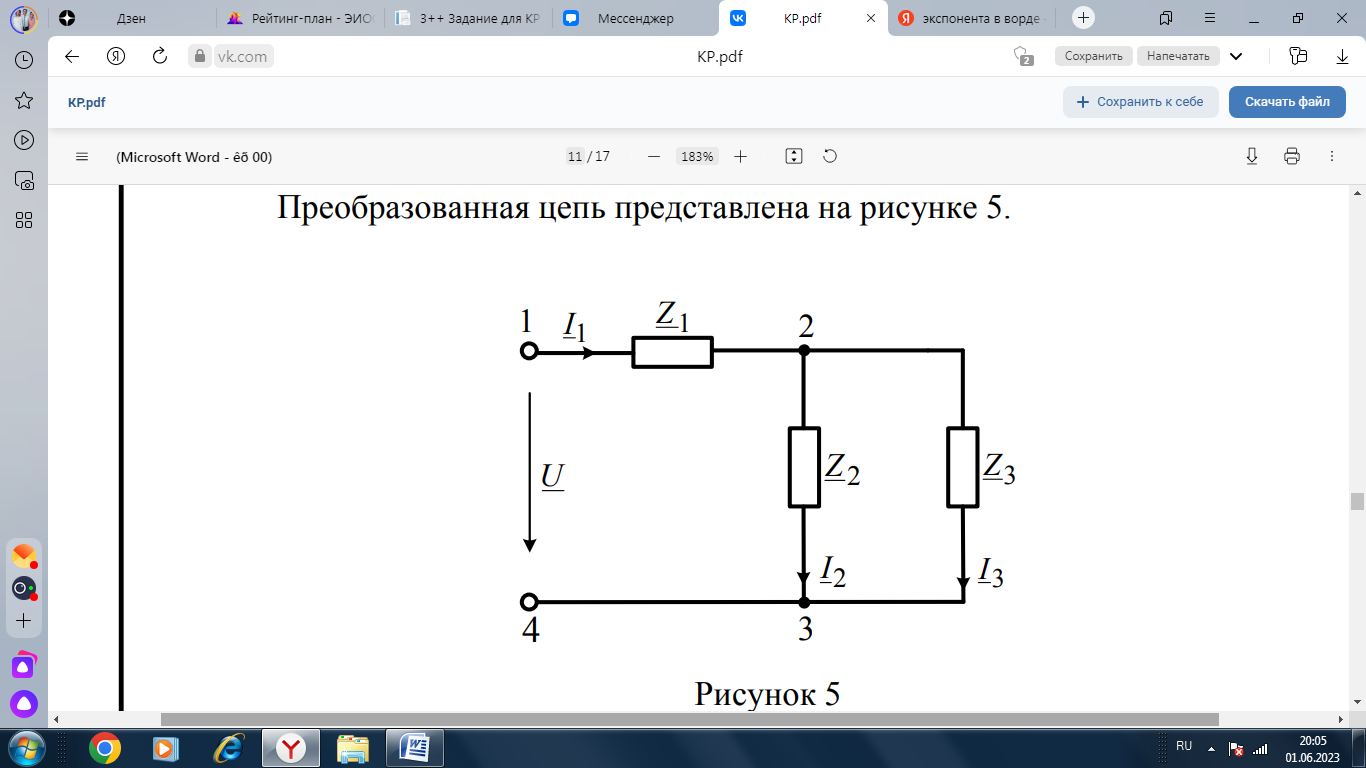
Рисунок 5
Осуществляем эквивалентные преобразования для цепи. Параллельно соединенные элементы
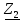и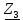 
заменяем одним эквивалентным 
:
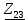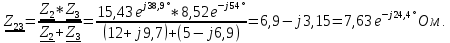
После преобразования схема упрощается и состоит из двух элементов, включенных последовательно (рисунок 6):
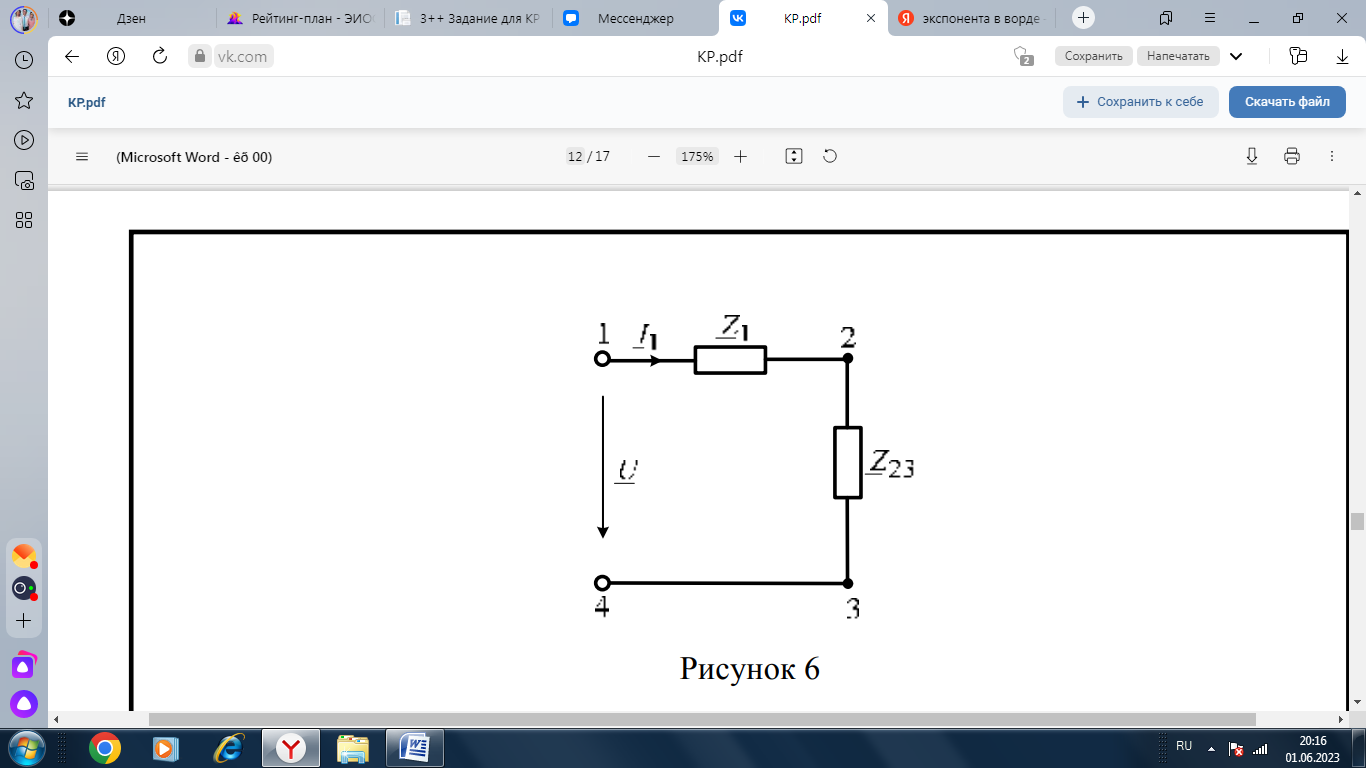
Рисунок 6
Определяем эквивалентное сопротивление всей цепи:
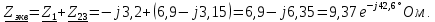
2. Общий ток цепи определяем по закону Ома:
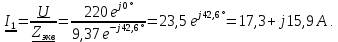
Определяем напряжение на участке 1-2 цепи:
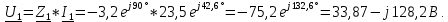
Определяем напряжение на участке 2-3 цепи:
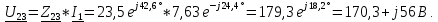
Определяем токи в ветвях после разветвления, используя закон Ома:
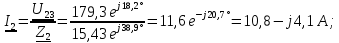
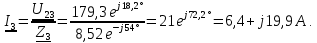
Для проверки найденных токов составим уравнение согласно первому закону Кирхгофа для узла 2 (рисунок 5):
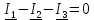
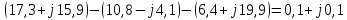
3. Запишем мгновенные значения токов ветвей:
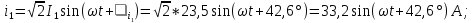
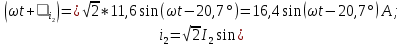
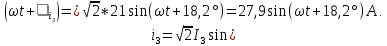
Запишем мгновенное значение напряжения на участке цепи с параллельным соединением ветвей:
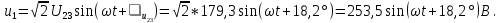
4. Составим баланс активных и реактивных мощностей. Эти балансы показывают, что активные и реактивные мощности на входе должны быть равны сумме соответственно активных и реактивных мощностей всех потребителей.
Комплексная мощность цепи с активным, индуктивным и емкостным сопротивлениями:
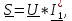
Где
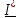сопряженный комплекс тока, А.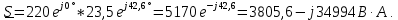
Активную мощность потребителей рассчитаем как произведение активного сопротивления участка, на квадрат действующего значения тока этого участка.
Суммарная активная мощность потребителей:
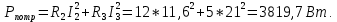
Реактивную мощность потребителей определяем как произведение квадрата тока реактивного элемента на его сопротивление. Причем мощность катушки индуктивности положительна, а конденсатора отрицательна.
Суммарная реактивная мощность потребителей:
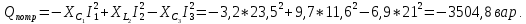
Таким образом, баланс активных и реактивных мощностей соблюдается.
5. Векторную диаграмму (рисунок 7) размещаем на комплексной плоскости с осями +1 и +j. Для построения векторной диаграммы выберем масштаб тока и напряжения m