Файл: Руководство по выполнению лабораторных работ по предмету Вычислительная математика.doc

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное Государственное бюджетное образовательное учреждение высшего профессионального образования

«ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ»

КАФЕДРА АВТОМАТИЗАЦИИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

Методическое руководство

по выполнению лабораторных работ

по предмету «Вычислительная математика»

с использованием математического пакета Маткад

Тюмень - 2013
Лабораторный практикум включает первоначальное знакомство с системой MATHCAD, семь лабораторных работ по разделам курса «Численные методы», каждая из которых имеет краткое описание метода, задания по вариантам и контрольные вопросы, а также фрагменты выполнения работ на MATHCAD. Практикум снабжен таблицами и литературой.

ВВЕДЕНИЕ
На персональном компьютере сегодня можно решать задачи научно-технических расчетов не прибегая к их кодированию на каком бы не было алгоритмическом языке (Бейсик, Паскаль, СИ). Использование интегрированных программных систем автоматизации математических расчетов (Eureka, MatLab, Maple, Mathematica, MathCAD и др.) позволяют решать поставленные задачи на входном языке, который максимально приближен к естественному математическому языку.

В MathCAD описание решения математических задач дается с помощью привычных математических формул и знаков. Такой же вид имеют и результаты вычислений. Так, что системы MathCAD вполне оправдывают аббревиатуру CAD (Computer Aided Disign), говорящую о принадлежности к сложным и продвинутым системам автоматизированного проектирования – САПР. MathCAD своего рода САПР в математике.

К задачам, решаемым в системе MathCAD, можно отнести:

• 
  подготовку научно-технических документов, содержащих текст, и формулы, записанные в привычной для специалистов форме;
  
• 
  вычисление результатов математических операций, в которых участвуют числовые константы, переменные и размерные физические величины;
  
• 
  операции с векторами и матрицами;
  
• 
  решение уравнений и систем уравнений (неравенств);
  
• 
  статистические расчеты и анализ данных;
  
• 
  построение двумерных и трехмерных графиков;
  
• 
  тождественные преобразования (в том числе упрощение), аналитическое решение уравнений и систем;
  
• 
  дифференцирование и интегрирование, аналитическое и численное;
  
• 
  решение дифференциальных уравнений;
  
• 
  проведение серий расчетов с различными значениями начальных условий и других параметров.
  

---

Технология работы в системе MATHCAD проста и удобна в работе.

Практикум включает первоначальное знакомство с системой, технологию работы, а также лабораторные работы, предусмотренные государственным стандартом.

Знакомство с системой MathCAD

Пользовательский интерфейс системы создан так, что пользователь, имеющий элементарные навыки работы с Windows-приложениями, может сразу начать работать с MathCAD.

Под интерфейсом понимается не только легкое управление системой, как с клавишного пульта, так и с помощью мыши, но и просто набор необходимых символов, формул, текстовых комментариев с последующим запуском документов (Worksheets) в реальном времени.

Запустив систему MathCAD из Windows, вы увидите на экране диалоговое окно, первоначально пустое (Рис. 1).

Р
ис. 1

Над ним видна строка с основными элементами интерфейса. Опции главного меню, содержащиеся в этой строке, легко изучит самостоятельно; некоторые из них очень похожи на стандартные опции, принятые в текстовых редакторах Windows.

Работа с документами MathCAD не требуют обязательного использования возможностей главного меню, так как основные из них дублируются кнопками быстрого управления, которые расположены в удобных перемещаемых с помощью мыши наборных панелях – палитрах. Наборные панели появляются в окне редактирования документов при активизации кнопок – пиктограмм. Они служат для вывода заготовок – шаблонов математических знаков (цифр, знаков арифметических операций, матриц, знаков интеграла, производных, приделов и др.). Указатель мыши подводим к “Вид” в главном меню, щелкаем левой кнопкой мыши; указатель подводим к “Панели инструментов” и щелкаем левой кнопкой мыши; Выпадает следующее меню. Указатель мыши подводим к “Математика” и щелкаем левой кнопкой мыши. Выпадают наборные панели. (Рис. 2)

Р
ис. 2
ВЫЧИСЛЕНИЯ И ОПЕРАЦИИ В MATHCAD

Приведем примеры решения некоторых типовых математических задач.

Примечание. Решение завершаем щелчком левой кнопки мыши, предварительно уводя указатель мыши за пределы выделенной области набора примера.

Пример 1. Упростить выражение:

---

a² – b² .

2a + 2b

Решение. В окне редактирования (далее на экране) набираем исходное выражение

Указатель мыши подводим к опции “Символы” в главном меню и щелкаем левой кнопкой мыши один раз (далее входим в “Символы”). В выпавшем меню указатель мыши подводим к опции “Упростить” и активизируем (щелчком левой кнопкой мыши) указанную опцию. На экране отображается наше выражение, но уже в выделенном виде. Повторяем наши действия: входим в “Символы” (подводим указатель мыши и щелкаем левой кнопкой мыши) и активизируем “Упростить”. На экране появляется ответ : a - b.

Пример 2. Вычислить: 10x² –5y² , при x=1,5 и y=-1,6.

Решение. На экране набираем; с клавиатуры набираем знак =, компьютер сам поставит знак :=.

x: =1.5 y: =-1.6

10^. x² – 5^. y²=

рядом со знаком равенства читаем ответ : 9.7.

Пример 3. Преобразуйте в многочлен: (a + 2^. b) ^. (a – 2^. b) ^. (a² + 4^. b²).

Решение. На экране набираем исходное выражение

(a + 2^. b) ^. (a – 2^. b) ^. (a² + 4^. b²)

Входим в меню “Символы”, активизируем “Расширить”. На экране читаем ответ:

a⁴ – 16^. b⁴ .

Пример 4. Разложите на множители: 4z⁴ – 25k².

Решение. На экране набираем

4^.z⁴ – 25^.k²

Входим в меню “Символы”, активизируем “Фактор”. На экране читаем ответ:

-(5^.k – 2^.z²)^.(5^.k² + 2^.z²).

Пример 5. Разложите на множители: 12x³ – 3x²y – 18xy².

Решение. На экране набираем 12^. x³ – 3^. x^2. y – 18^. x ^. y² .

Входим в меню “Символы”, активизируем “Фактор”. На экране читаем ответ:

3^. (4^. x² – x^. y –6 ^. y²).
Пример 6. Сократите дробь: x² – 2^.m^.x+ 3^.x - 6^.m .

x² + 2^. m^. x + 3^. x + 6^. m

Решение. На экране набираем исходное выражение.

Входим в меню “Символы”, активизируем “Упростить”. На экране читаем ответ: (x – 2^.m) .

(x + 2^. m)

Пример 7. Вычислите: 36^-1/2 .

27^1/3 – 81^{1/4 .} 5

Решение. На экране набираем искомый пример. Ставим знак равенства и читаем ответ: -0. 014.

---

Пример 8. Решите уравнение: 2^. (5^. x – 1)² + 35^. x – 11 = 0.

Решение. Аналитическое решение. Набираем ключевое слово given (дано).

Вводим уравнение 2^. (5^. x – 1)² + 35^. x – 11 = 0. Здесь при вводе знака =, мы вводим знак - логическое равно из палитры, а не с клавиатуры.

Набираем find(x), рядом читаем решение:

- 3 3

5 10

Пример 9. Решите уравнение: y³ + 6^. y² – 16^. y = 0.

Решение. Численный поиск корней уравнения.

Для поиска корней искомой переменной, надо присвоить начальное значение, а затем при помощи вызова функции root(f(x),x) находим корень.

Набираем на экране

y:=1

root(y³ + 6^. y² – 16^. y, y)=

читаем ответ: -8.

Если в качестве начального значения возьмем y:=-2, то получим ответ: 0.

Пример 10. Решите систему уравнений:

x² + y +8 = x^. y

y – 2^. x = 0.

Решение. Набираем ключевое слово given и систему уравнений

x² + y +8 = x^. y

y – 2^. x = 0.

Между левыми и правыми частями уравнений ставим знак логическое равно = .Набираем вызов функции find(x,y), читаем на экране ответ:

-2 4

-4 8

Пример 11. а) Решите неравенство: 5^. x – 3 =< 4.

Решение. На экране набираем неравенство и входим в палитру “Символические операторы”, активизируем “solve”, набираем x

5^. x – 3 =< 4 solve, x 

на экране читаем ответ: x=< 7/5.

б) Решите неравенство: 2^. a² – 5 < 15.

На экране набираем неравенство и входим в палитру “Символические операторы”, активизируем “solve”, набираем а

2^. a² – 5 < 15 solve, a 

на экране читаем ответ:(- 10 10).

Пример 12. Вычислите: cos 34^{0 .} cos 56⁰ – sin 34^{0 .}sin 124⁰.

Решение. Набираем на экране

cos (34 ^. deg) ^. cos (56 ^. deg) – sin (34 ^. deg) ^. sin (124 ^. deg)=

и читаем ответ: 0.

Примечание. Набираем deg, если угол задан в градусах; rad – в радианах.

Пример 13. Построить график функции y=2 ^. sin 2^. x.

---

Решение. Набираем на экране y(x):=2 ^. sin (2^. x). Отводим указатель мыши от выделенной части и щелкаем левой кнопкой мышки. Указатель мыши подводим к “Построение графиков” и входим, активизируем “Декартов график”. Появляется шаблон для построения графика. На ней выделены метки. Указатель мыши подводим к нижней метке, активизируем. Набираем x. Появляются по горизонтали еще две метки, где мы должны указать интервалы построения графика. Указатель мыши подводим к левой метке, щелкая левой кнопкой мыши активизируем и вводим левую границу 0. Указатель мыши подводим к правой границе, активизируем и вводим 5. Уводим указатель мыши к метке оси Y, активизируем его и вводим y(x). Появляются метки нижней и верней границ оси Y. В нижней набираем –2, в верхней 2. Отводим указатель мыши от шаблона для графиков, щелкаем левой кнопкой мыши. Появляется искомый график. Для форматирования графика нужно дважды щелкнуть в области графика. В выпавшем меню м
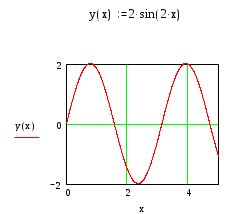
ожно управлять отображением линий, масштабом и др.
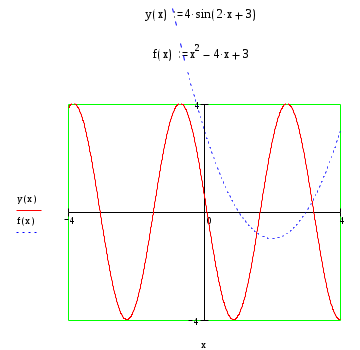
Пример 14. Построить графики функций:

y(x)=4sin(2 x +3) и f(x)=x²-4x+3.

Решение. Решение аналогично предыдущему примеру. В шаблоне для построения графиков имена функций набираем через запятую. Ограничений для значений аргументов и функций не ставим. Далее щелкаем мышью вне поля графиков.



Пример 15. Построить график функций z=sin(x²+y²) для x от –2 до 2 и y от –2 до 2. Фрагмент выполнения задания приведен ниже.





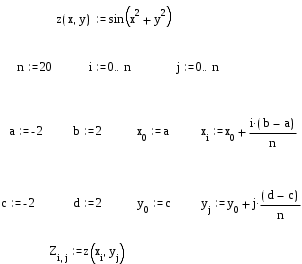
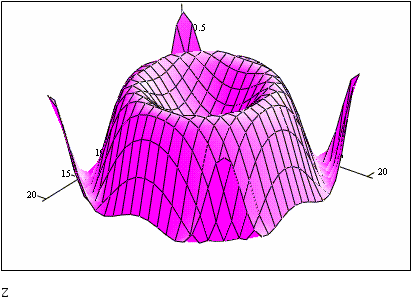
Пример 16. Вычислите предел многочлена: 2^. x³ – 3^. x² +3.

Решение. Из палитры “Высшей математики”, активизируем lim, заполняем выведенный шаблон; завешаем набор знаком  палитры “Операторы отношений”. На экране читаем ответ: 7.

Пример 17. Вычислите производную: cos x + x^. sin x.

Решение. Из палитры “Высшей математики”, активизируем , заполняем выведенный шаблон; завешаем набор знаком  палитры “Операторы отношений”. На экране читаем ответ: x^.

---