Файл: Лекции Звуковые волны Звуковые волны Эффект Доплера.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 57
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- оператор Лапласа, υ – фазовая скорость.
Всякая функция, удовлетворяющая этим уравнениям, описывает некоторую волну. Следовательно, электромагнитные поля действительно могут существовать в виде электромагнитных волн.
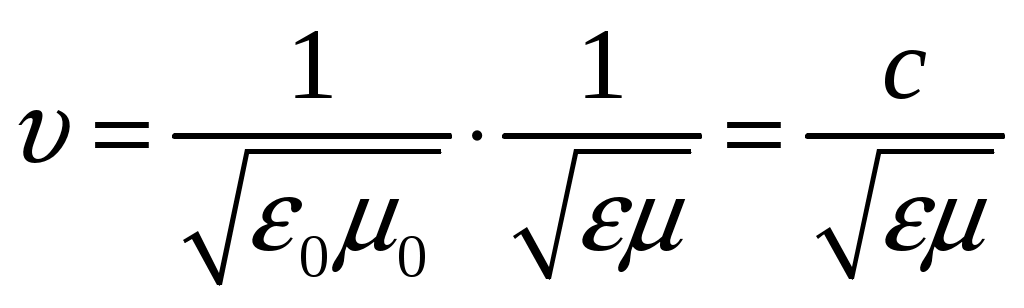 , (3)
, (3)
Где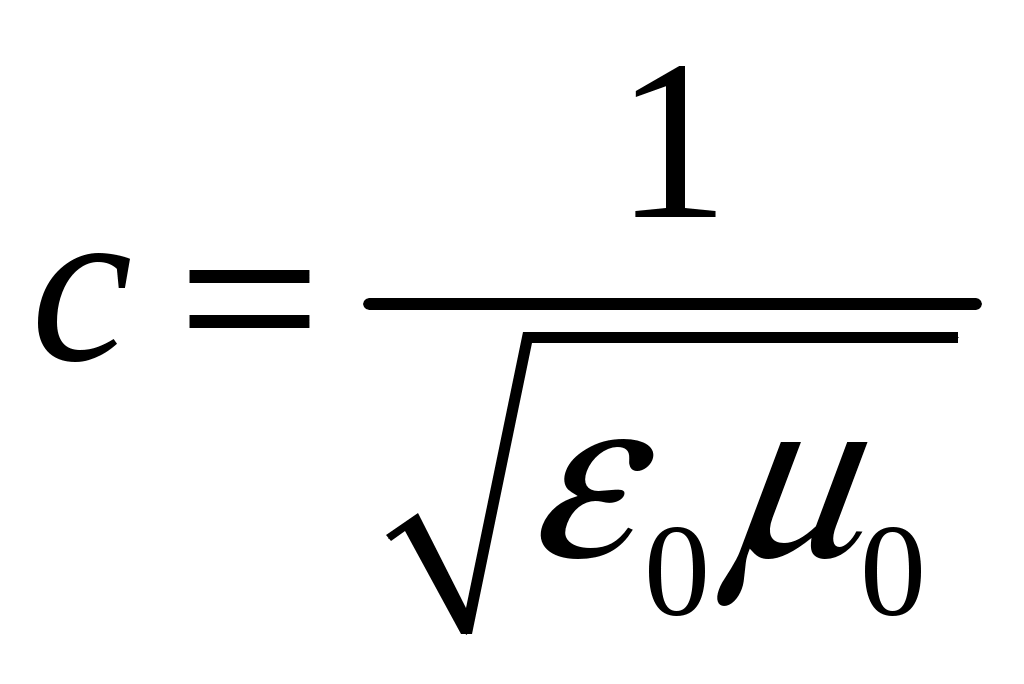 - скорость электромагнитных волн в вакууме,
- скорость электромагнитных волн в вакууме,
ε0, μ0- электрическая и магнитная постоянные,
ε, μ- электрическая и магнитная проницаемость среды.
При вычислении скорости распространения электромагнитного поля по формуле (3) получается результат, достаточно хорошо совпадающий с экспериментальными данными, если учитывать зависимость ε и μ, от частоты.
С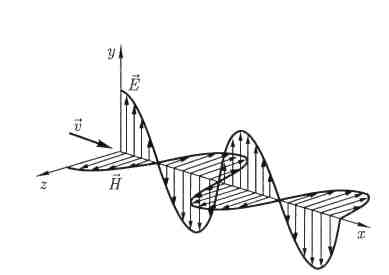 овпадение же размерного коэффициента в (3) со скоростью распространения света в вакууме указывает на глубокую связь между электромагнитными и оптическими явлениями, позволившую Максвеллу создать электромагнитную теорию света, согласно которой свет представляет собой электромагнитные волны.
овпадение же размерного коэффициента в (3) со скоростью распространения света в вакууме указывает на глубокую связь между электромагнитными и оптическими явлениями, позволившую Максвеллу создать электромагнитную теорию света, согласно которой свет представляет собой электромагнитные волны.
3. Следствием теории Максвелла является также поперечность электромагнитных волн: векторы и
и  напряженностей электрического и магнитного полей волны взаимно перпендикулярны (на рис. 229 показана моментальная «фотография» плоской электромагнитной волны) и лежат в плоскости, перпендикулярной вектору υскорости распространения волны, причем векторы
напряженностей электрического и магнитного полей волны взаимно перпендикулярны (на рис. 229 показана моментальная «фотография» плоской электромагнитной волны) и лежат в плоскости, перпендикулярной вектору υскорости распространения волны, причем векторы  ,
,  и
и
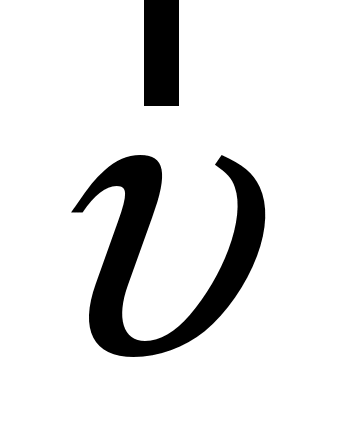 образуют правовинтовую систему.
образуют правовинтовую систему.
В фиксированной точке пространства векторы и
и  изменяются со временем по гармоническому закону:
изменяются со временем по гармоническому закону:
Такие изменения векторов и
и  происходят во всех точках пространства, но со сдвигом по фазе, определяемым расстоянием между точками, отсчитанными вдоль оси х.
происходят во всех точках пространства, но со сдвигом по фазе, определяемым расстоянием между точками, отсчитанными вдоль оси х.
4. Из уравнений Максвелла следует также, что в электромагнитной волне векторы и
и  всегда колеблются в одинаковых фазах(см. рис. 229), причем мгновенные значения E Н влюбой точке связаны соотношением
всегда колеблются в одинаковых фазах(см. рис. 229), причем мгновенные значения E Н влюбой точке связаны соотношением
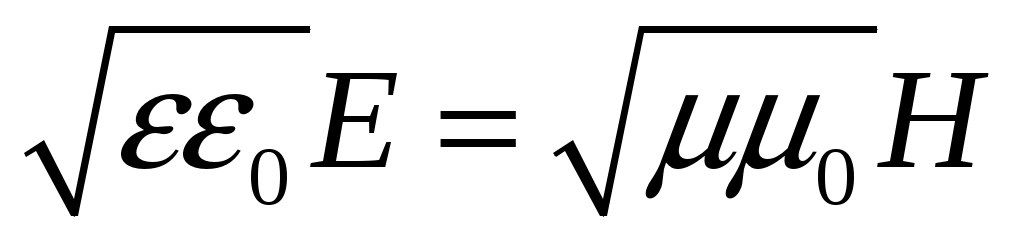
(4)
Следовательно, Е и Н одновременно достигают максимума, одновременно обращаются в нуль. От уравнений (1) можно перейти к уравнениям
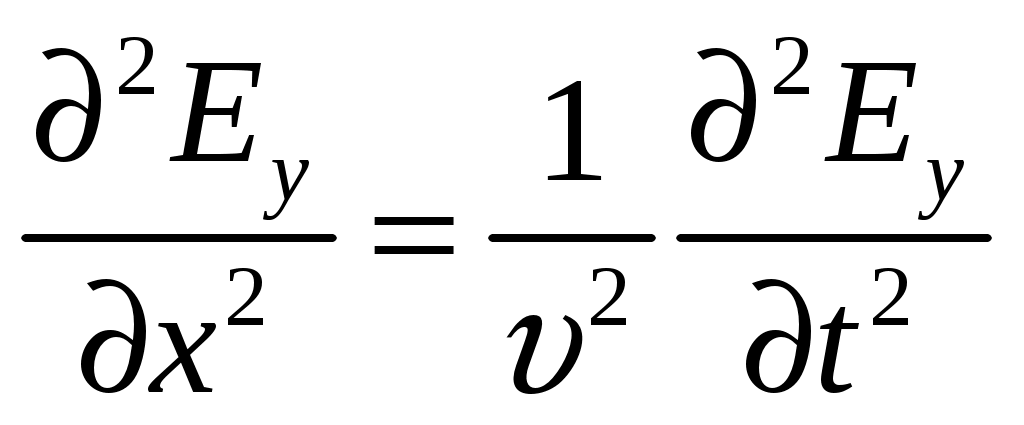 ,
, 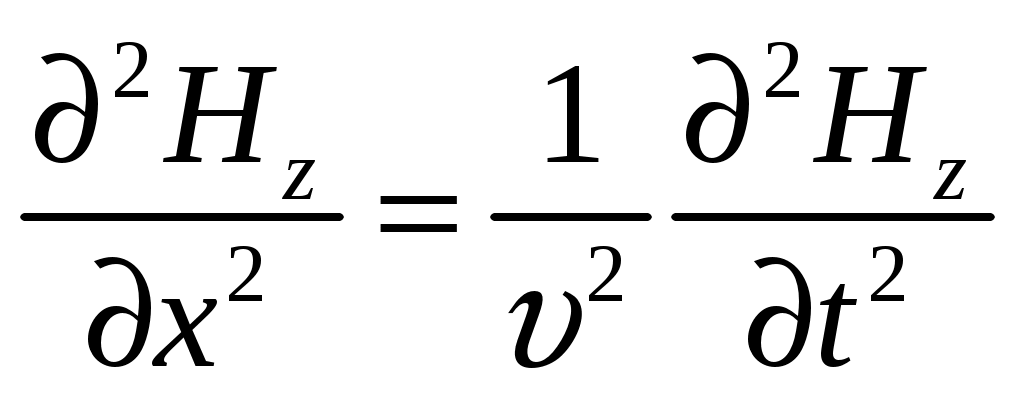 , (5, 6)
, (5, 6)
где соответственно индексы у и zпри Е и Н подчеркивают лишь то, что векторы и
и  направлены вдоль взаимно перпендикулярных осей у иz.
направлены вдоль взаимно перпендикулярных осей у иz.
Уравнениям (5) и (6) удовлетворяют, в частности, плоские монохроматические электромагнитные волны (электромагнитные волны одной строго определенной частоты), описываемые уравнениями
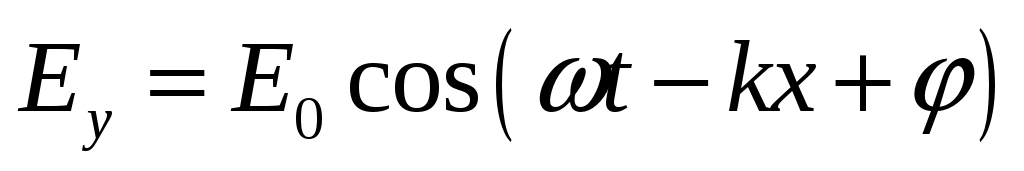 ,
, 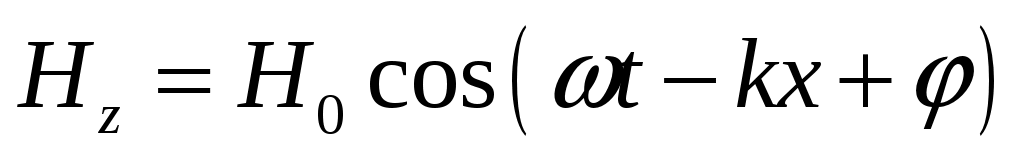 (7, 8)
(7, 8)
где Е0и Н0— соответственно амплитуды напряженностей электрического и магнитного полей волны; ω — круговая частота волны; k - волновое число;
φ — начальные фазы колебаний в точках с координатой х = 0.
В уравнениях (7) и (8) φ одинаково, так как колебания электрического и магнитного векторов в электромагнитной волне происходят в одинаковых фазах.
5. Энергия и импульс электромагнитной волны
Возможность обнаружения электромагнитных волн указывает на то, что они переносят энергию.
Объемная плотность wэнергии электромагнитной волны складывается из объемных плотностей: w элэлектрического и w м магнитного полей:
w = w эл + w м =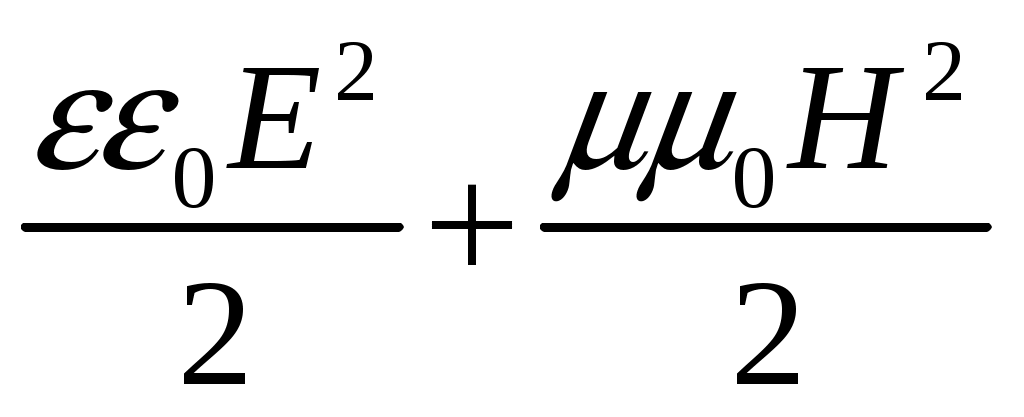
Учитывая выражение (4), полу
чим, что объемные плотности энергии электрического и магнитного полей в каждый момент времени одинаковы, т.е. wэл = wм. .
Поэтому можно записать w = 2 wэл =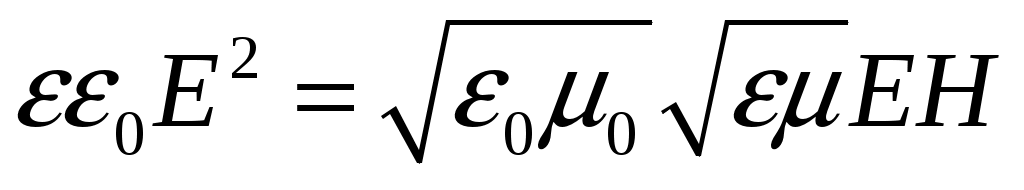
Умножив плотность энергии wна скорость υраспространения волны в среде [см. (3)], получим модуль плотности потока энергии:
S= wυ = EH.
Так как векторы и
и  взаимно перпендикулярны и образуют с направлением распространения волны право-винтовую систему, то направление вектора [
взаимно перпендикулярны и образуют с направлением распространения волны право-винтовую систему, то направление вектора [
 ] совпадает с направлением переноса энергии, а модуль этого вектора равен EH.
] совпадает с направлением переноса энергии, а модуль этого вектора равен EH.
Вектор плотности потока электромагнитной энергииназывается вектором Умова— Пойнтинга:
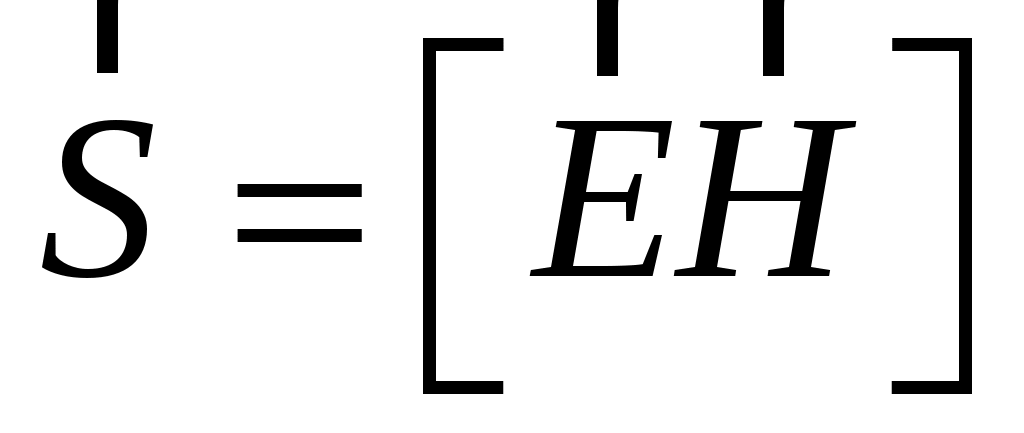
Вектор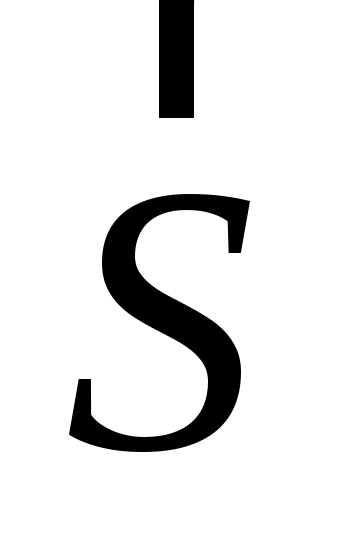
Если электромагнитные волны поглощаются или отражаются телами (эти явления подтверждены опытами Герца), то из теории Максвелла следует, что электромагнитные волны должны оказывать на тела давление.
Давление электромагнитных волн объясняется тем, что под действием электрического поля волны заряженные частицы вещества начинают упорядоченно двигаться и подвергаются со стороны магнитного поля волны действию сил Лоренца.
В исключительно тонких экспериментах ставших классическими, П. Н. Лебедев 1899 г. доказал существование светового давления на твердые тела, а в 1910 г. — на газы. Опыты П.Н. Лебедева имели огромное значение для утверждения выводов теории Максвелла о том, что свет представляет собой электромагнитные волны. Существование давления электромагнитных волн приводит к выводу о том, что им присущ механический импульс. Электромагнитная волна, несущая энергию W, обладает импульсом
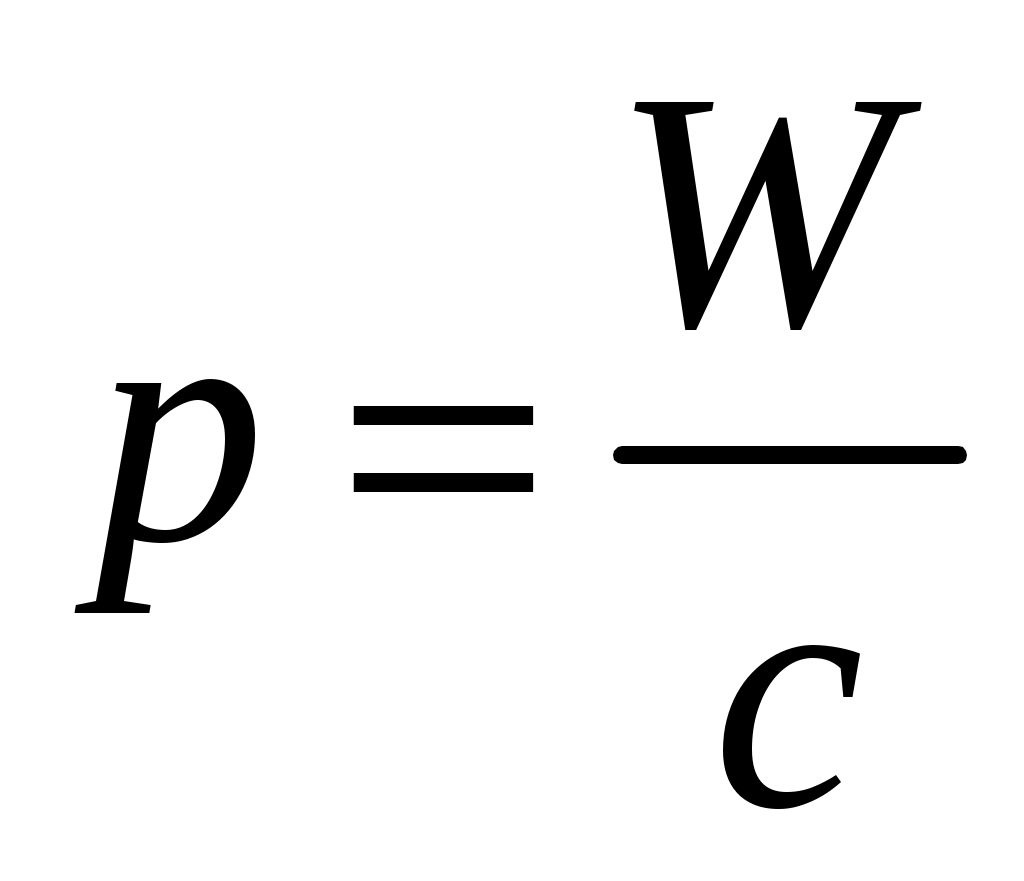 .
.
Всякая функция, удовлетворяющая этим уравнениям, описывает некоторую волну. Следовательно, электромагнитные поля действительно могут существовать в виде электромагнитных волн.
-
Фазовая скорость электромагнитных волн определяется выражением
Где
ε0, μ0- электрическая и магнитная постоянные,
ε, μ- электрическая и магнитная проницаемость среды.
-
В вакууме (при ε = 1 и μ = 1) скорость распространения электромагнитных волн совпадает со скоростью с. -
В веществе εμ> 1, поэтому скорость распространения электромагнитных волн в веществе всегда меньше, чем в вакууме.
При вычислении скорости распространения электромагнитного поля по формуле (3) получается результат, достаточно хорошо совпадающий с экспериментальными данными, если учитывать зависимость ε и μ, от частоты.
С
 овпадение же размерного коэффициента в (3) со скоростью распространения света в вакууме указывает на глубокую связь между электромагнитными и оптическими явлениями, позволившую Максвеллу создать электромагнитную теорию света, согласно которой свет представляет собой электромагнитные волны.
овпадение же размерного коэффициента в (3) со скоростью распространения света в вакууме указывает на глубокую связь между электромагнитными и оптическими явлениями, позволившую Максвеллу создать электромагнитную теорию света, согласно которой свет представляет собой электромагнитные волны.3. Следствием теории Максвелла является также поперечность электромагнитных волн: векторы
В фиксированной точке пространства векторы
-
t= 0 . оба вектора одновременно увеличиваются от нуля -
t= ¼T. через ¼ периода достигают наибольшего значения: если направлен вверх, то
направлен вверх, то  направлен вправо (смотрим вдоль направления распространения волны );
направлен вправо (смотрим вдоль направления распространения волны ); -
t= ½ T.через ¼ периода оба вектора одновременно обращаются в нуль. -
t= ¾ T.через ¼ периода достигают наибольшего значения, но теперь: если направлен вниз, то
направлен вниз, то  направлен влево.
направлен влево. -
t= T. По завершении периода оба вектора обращаются в нуль.
Такие изменения векторов
4. Из уравнений Максвелла следует также, что в электромагнитной волне векторы
(4)
Следовательно, Е и Н одновременно достигают максимума, одновременно обращаются в нуль. От уравнений (1) можно перейти к уравнениям
где соответственно индексы у и zпри Е и Н подчеркивают лишь то, что векторы
Уравнениям (5) и (6) удовлетворяют, в частности, плоские монохроматические электромагнитные волны (электромагнитные волны одной строго определенной частоты), описываемые уравнениями
где Е0и Н0— соответственно амплитуды напряженностей электрического и магнитного полей волны; ω — круговая частота волны; k - волновое число;
φ — начальные фазы колебаний в точках с координатой х = 0.
В уравнениях (7) и (8) φ одинаково, так как колебания электрического и магнитного векторов в электромагнитной волне происходят в одинаковых фазах.
5. Энергия и импульс электромагнитной волны
Возможность обнаружения электромагнитных волн указывает на то, что они переносят энергию.
Объемная плотность wэнергии электромагнитной волны складывается из объемных плотностей: w элэлектрического и w м магнитного полей:
w = w эл + w м =
Учитывая выражение (4), полу
чим, что объемные плотности энергии электрического и магнитного полей в каждый момент времени одинаковы, т.е. wэл = wм. .
Поэтому можно записать w = 2 wэл =
Умножив плотность энергии wна скорость υраспространения волны в среде [см. (3)], получим модуль плотности потока энергии:
S= wυ = EH.
Так как векторы
Вектор плотности потока электромагнитной энергииназывается вектором Умова— Пойнтинга:
Вектор
-
направлен в сторону распространения электромагнитной волны, -
его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.
Если электромагнитные волны поглощаются или отражаются телами (эти явления подтверждены опытами Герца), то из теории Максвелла следует, что электромагнитные волны должны оказывать на тела давление.
Давление электромагнитных волн объясняется тем, что под действием электрического поля волны заряженные частицы вещества начинают упорядоченно двигаться и подвергаются со стороны магнитного поля волны действию сил Лоренца.
В исключительно тонких экспериментах ставших классическими, П. Н. Лебедев 1899 г. доказал существование светового давления на твердые тела, а в 1910 г. — на газы. Опыты П.Н. Лебедева имели огромное значение для утверждения выводов теории Максвелла о том, что свет представляет собой электромагнитные волны. Существование давления электромагнитных волн приводит к выводу о том, что им присущ механический импульс. Электромагнитная волна, несущая энергию W, обладает импульсом