Задача 6.29.0
Цилиндрическая цистерна наполнена авиационным бензином, температура которого 20 ºС. Диаметр цистерны D, длина L. Определить силы давления на плоские торцевые стенки А и В цистерны в двух случаях: 1) когда цистерна не движется; 2) при движении цистерны горизонтально с положительным ускорением α.



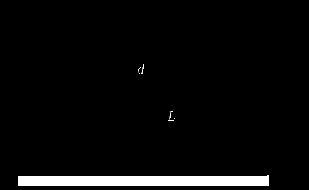
Рис. 7
Таблица 2

Предпоследняя цифра шифра
8	2,1	3,8	0,28	8,49

Решение
1 Цистерна не движется
Силу давления на плоские торцевые стенки и определяем по формуле:

(1)

где - избыточное гидростатическое давление в центре тяжести торцевой стенки цистерны площадью , ;

(2)

Подставляя выражение (2) в выражение (1), получаем

(3)

- площадь круглого торца цистерны, ;

---

(4)

Подставляя выражение (4) в выражение (3), получаем

(5)

где - глубина погружения центра тяжести рассматриваемой плоской фигуры под пьезометрической поверхностью (так как давление на свободной поверхности жидкости равно атмосферному, то пьезометрическая плоскость совпадает со свободной поверхностью), ;

(6)

Подставляя выражение (6) в выражение (5), получаем

(7)

- плотность бензина при , ;

- ускорение свободного падения, ;





Рисунок 11.1

2 Цистерна движется горизонтально с положительным ускорением а
При горизонтальном движении цистерны с ускорением пьезометрическая плоскость наклонится к горизонту под углом , определяемым из условия:

(8)



Определяем величину , на которую опустится бензин у передней стенки

---

и поднимется у задней стенки :

(9)


Сила давления на плоскую торцевую стенку :

(10)

где - глубина погружения центра тяжести смоченной поверхности стенки , ;

(11)

- площадь смоченной поверхности стенки , ;

(12)

Подставляя выражение (12) и (11) в выражение (10), получаем

(13)



Сила давления на плоскую торцевую стенку :

(14)

где - глубина погружения центра тяжести смоченной поверхности стенки , ;

(15)

---

- площадь кругового сегмента стенки , ;

(16)

- угол разворота дуги, ;

(17)



Подставляя полученное значение в формулу (16), получаем



Длина хорды:

(18)


Подставляя полученные значение в формулу (15), получаем


По формуле (14), находим





Рисунок 11.2
Ответ: 1) ; 2) , .

---

Смотрите также файлы

• Химический элементэто определенный вид атомов, имеющих одинаковый заряд ядра и количество электронов.docx

• 1. Чему равен 1 КбайтС.docx

• Бухгалтерский учет по налогам и сборам.pptx

• Государственное профессиональное образовательное учреждение.docx

• Программа среднего профессионального образования 44. 02. 01 Дошкольное образование Дисциплина Ручное практическое задание до, СпДО.rtf