Файл: Частное образовательное учреждение высшего образования региональный открытый социальный институт.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Отчет по практике

Дисциплина: Не указана

Добавлен: 26.10.2023

Просмотров: 39

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Оглавление



В связи с вышеизложенным актуальной является научно-техническая задача многократного повышения скорости выполнения процедур планирования размещения параллельно обрабатываемых задач по процессорам кластерной системы путем реализации названных процедур в специализированном вычислительном устройстве.

Разработанный метод ускорения поиска субоптимального варианта размещения задач по процессорам базового матричного кластерного блока основан на следующем подходе.

Пакет взаимодействующих программ (задач), запланированных к обработке в базовом блоке, аописывается графом взаимодействия задач

G=, где  а - аа (1)

множество вершин графа G, вершины  акоторого соответствуюта задачам, а дуги связей между ними  апри  авзвешиваются объёмами данных  , передаваемыми между задачами и сведенными в матрицу обмена информацией (МОИ)  , где  .

Матричный базовый блок кластерной системы представляется топологической моделью в виде графа H=
, где  а - множество идентификаторова процессорных модулей базового блока, организованных в матрицу |P|n?n, где  а- число процессорных модулей базового блока;   - множество межмодульных связей, задаваемых матрицей смежности  аразмером  .

Размещение пакета программ (задач), описываемых графом G (1), в параллельной системе (ПС) может быть аналитически описано отображением

,

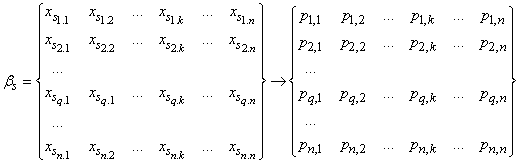где  ,  ,  .
(2)

Здесь  а - это номер очередной перестановки задач  апо процессорным модулям  , соответствующий  -му варианту размещения. Мощность множества  авсевозможных отображений (2) равна числу всевозможных перестановок задач  ав матрице  : . Для описания множества длин  акратчайших маршрутов передачи данных в пределах базового блока введем матрицу минимальных расстояний (ММР)  ,  , которая строится по матрице смежности.

Задачу планирования размещения, можно сформулировать как поиск такого отображения b*IY, что

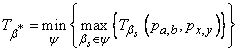, (3)

где а а - коммуникационная задержка при передаче данных между процессорными модулями  аи  , соответствующая отображению  аи вычисляемая как произведение

,а (4)

где  аи  ,

а  .аа (5)

Присутствующий в (4) сомножитель С не учитывается в выражениях (3,5) и последующем анализе, так как он обратно пропорционален постоянной скорости передачи данных и поэтому не влияет на результаты минимизации по (3).

Поиск наилучшего варианта размещения b* по критерию (3) является сложной переборной задачей. Одним из путей его ускорения может быть применение целенаправленных перестановок строк и столбцов матрицы МОИ с выбором в ней aк-го места перестановки ее элемента  апо критерию:

, аа (6)

где  а - одноименные элементы матрицы ММР;  а - элемент МОИ, которому соответствует  , найденный в предыдущем шаге перестановок.

Новизна подхода состоит в том, что общее число требуемых перестановок можно дополнительно уменьшить, если отбросить явно нецелесообразные из них, разрешая очередную перестановку по следующим дополнительным критериям:

,аа (7)

.аа (8)

Многократное ускорение поиска возможно за счет допустимого снижения выигрыша на снижение величины коммуникационной задержки, например, не более, чем на 20-30%, по сравнению с лучшими результатами, достигаемыми при больших затратах времени на поиск. Для этого необходимо в ходе поиска контролировать степень уменьшения величины образующейся коммуникационной задержки (3) и принимать решение о целесообразности продолжения поисковых перестановок строк и столбцов матрицы МОИ. Процедура принятия решения основана на вычислении недостижимой минимальной оценки размещения Tinf (гипотетического минимума коммуникационной задержки) при допущении, что топологии графов G и H тождественны. При вычислении нижней оценки будем назначать дуги графа G с наибольшим весом  ана самые короткие маршруты в графе H, не обращая внимания на ограничения, накладываемые фактическими связями между задачами в графе G. Соответствующий формализованный алгоритм выглядит следующим образом.

  • Переписать элементы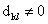  аматрицы D в вектор-строку  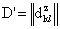атак, что  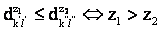, где z1 и z2 - порядковые номера элементов в D'.

  • Переписать элементы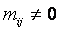  аматрицы M в вектор-строку  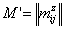атак, что  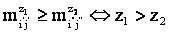, где z1 и z2 - порядковые номера элементов в M'.

  • Положить

,

гдеа  , а   - мощность множества E, равная количеству дуг в графе G;  ,  а - одноименные элементы векторов  аи  ас одинаковыми порядковыми номерами от начала названных выше векторЦстрок.

Для многократного ускорения поиска разработана следующая методика ускоренного выполнения процедур планирования размещения задач.

1. Составляются две матрицы: обмена информацией между задачами (МОИ) и кратчайших маршрутов (ММР) между процессорами в коммуникационной среде базового блока.

2. Вычисляются гипотетический минимум коммуникационной задержки Tinf и коэффициент эффективности исходного произвольного размещения задач  =Tн/Тinf.

3. По порогу эффективности  апринимается решение о целесообразности инициализации процедуры поиска субоптимального размещения. Под коэффициентом эффективности перестановок  апонимается отношение реально полученной величины задержки (5) к гипотетической  .

4. Выполняются шаги целенаправленных перестановок столбцов и строк матрицы обмена информацией. Находится максимальное значение коммуникационной задержки (5) по предыдущему варианту перестановок задач.

5. Находится минимум (3) из максимумов задержек по всем вариантам перестановок и вычисляется коэффициент эффективности  .

6. Если  аоказывается менее установленного порога эффективности  , шаги поиска прекращаются и найденный вариант матрицы обмена информацией считается соответствующим субоптимальному размещению.

Величина порога эффективности  , выбрана в результате статических исследований на программной модели алгоритма функционирования АПР.

На основании разработанных в данной главе метода ускорения поиска и методики ускорения выполнения процедур планирования размещения составлен следующий алгоритм, программноЦаппаратно реализованный в двухуровневом микропроцессорном акселераторе.

  • Ввести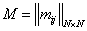  , 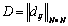 ,  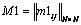,  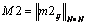,  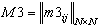,  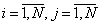а"mij=0, "m1ij=0, "m2ij=0, "m3ij=0.

2. Переписать "mij в  = ас изменением порядка следования элементов так, что  , где z1 и z2 порядковые номера элементов  .

3. Переписать "dij в  = ас изменением порядка следования элементов так, что  , где z1 и z2 порядковые номера элементов  .

Положить  , где  ,  .

5. Найти  , где N - число задач.

6. Вычислить  . Если  , то останов, иначе перейти к п.7.

7. Принять Т0=Тн.

8. Выполнить  :  .

9. Принять k=1.

10. Выбрать  аиз  .

11. Найти  аиз M2 такой, что  , и - соответствующий ему  аиз D.

12. Если  =1, то  , k=k+1 и перейти к п.10, иначе п.13;

13. Принять i=1.

14. Если  , то перейти к п. 15, иначе - п.25.

15. Если  аи  аи  , то перейти к п.16, иначе i=i+1 и - п.14.

16. Для  авыполнить операцию  аи сформировать  :

,  ,

,  ,

,  ,  .

17. Вычислить  . Если  , то перейти к п.18, иначе  аи - п.14.

18. Вычислить 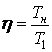 . Если  , то останов и выдача М1, иначе перейти к п.19.

19. Принять  :  .

20. Принять Т0=Т1.

21. Принять  .

22. Для  авыполнить операцию  аи сформировать  :

,  ,

,  ,

,  ,  .

23. Принять  :  .

24. Принять k=k+1 и перейти к п.26.

25.  , k=k+1.

26. Если  , то останов и выдача М1, иначе перейти к п.9

В третьей главе описаны программная модель разработанного алгоритма планирования размещения задач и результаты статистических исследований его эффективности.

Для моделирования и тестирования разработанного метода планирования размещения задач в кластерных системах была разработана на языке Си++ программная система, котораяа позволяет программно реализовать алгоритм размещения, строить графики изменения показателей эффективности  аи  апри каждой пробной перестановке и с заданной точностью фиксировать время расчета.

Целью исследования было определение величины выигрыша  ав снижении задержки в результате применения разработанного метода при разных видах и степенях заполнения МОИ, соответствующих широкому диапазону изменения степени связности между задачами пакета программ, запланированных к обработке в базовом матричном блоке. Результаты, соответствующие матрице наилучшего размещения  , начальному и достигнутому отклонению задержки Т от Tinf:  аи  асоответственно, достигнутому выигрышу s в разах, а так же времени, затраченному на поиск, выводятся на экран.

Смотрите также файлы