Файл: Вопрос Какие средства исследований применяют в швейном производстве при изучении и контроле технологических процессов, сырья, полуфабрикатов и готовых изделий, разработке новых моделей.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 104
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
n=14 и критического уровня α=0,05 интервал Анижн и Аверх, который составляет 27<А<63. Полученное значение А=31 попадает в указанный интервал, а это значит – нет ухода систематической погрешности.
Задача 1. Проверьте гипотезу об отсутствии ухода систематической погрешности (оцените, не происходит ли изменений в показаниях прибора). Уровень значимости α = 0,05%.
Решение. Предположим, что случайная величина срока безотказной работы подчинена нормальному закону распределения. Требуется проверить гипотезу о числовом значении математического ожидания нормально распределенной величины (генеральной средней) при неизвестной генеральной дисперсии. В этом случае в качестве критерия выбирают функцию
,
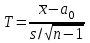где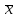
– выборочная средняя, а0 – математическое ожидание, s – выборочное среднее квадратичное отклонение. Случайная величина Т имеет t-распределение (распределение Стьюдента) с 
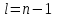степенями свободы.
Требуется найти критическую область для нулевой гипотезы Н0: а0=0,05 при альтернативной гипотезе Н1: а1<2900. Очевидно, что другие альтернативные гипотезы (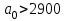
и 
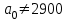) нецелесообразны, т.к. потребитель обычно обеспокоен лишь тем, что срок службы изделия может оказаться меньше гарантируемого поставщиком.
Критическая область левосторонняя;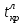
находим из условия 
.
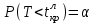Задача 2. Определите, имеются ли грубые погрешности (выбросы) среди результатов многократных измерений, указанных в задаче № 1, при доверительной вероятности Р = 0,95 (95%), используя Критерий Граббса.
Расчеты выполнить с использованием Microsoft Office Excel
Решение
Следует проверить, является ли эта погрешность систематической.
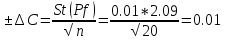
С -доверительный интервал концентраций.
S - стандартное отклонение, рассчитанное из 20 параллельных измерений концентрации
f - коэффициент Стъюдента, при Р=0,95, n=20
Разность среднего результата анализа и паспортного значения концентрации стандартного образца, взятого для исследования, больше доверительного интервала. Следовательно, методика отягощена систематической погрешностью.
Задача 3. Для выборки, приведенной в задаче № 1 с учетом удаления выбросов, определите случайную погрешность результатов измерений при доверительной вероятности Р = 0,95.
Расчеты выполнить с использованием Microsoft Office Excel
Представить методику расчета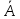
, S,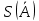 
, 
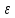и выбор t - коэффициент Стьюдента
Решение
Доверительные границы случайной погрешности вычисляются при доверительной вероятности P = 0,95, а также при P = 0,99, если измерения в дальнейшем повторить нельзя:
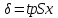
где tp – коэффициент Стьюдента, определяемый по табл. П.4 при заданной доверительной вероятности P и числе степеней свободы k. Для прямых измерений
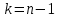
Границы неисключенной систематической погрешности
В качестве составляющих неисключенной систематической погрешности рассматриваются погрешности метода, погрешности средств измерений (например, пределы допускаемой основной и дополнительных погрешностей, если их случайные составляющие пренебрежимо малы) и погрешности, вызванные другими источниками. При суммировании составляющих неисключенные систематические погрешности средств измерений рассматриваются как случайные величины. Если их распределение неизвестно, то принимается равномерное распределение, и тогда границы неисключенной систематической погрешности результата при числе составляющих m > 4 определяют как
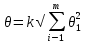
где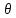
– границы отдельных составляющих общим числом m;
k – коэффициент, равный 1,1 при доверительной вероятности P = 0,95 и 1,4 при P = 0,99. Если же число суммируемых погрешностей m £ 4, то коэффициент k определяется по графику
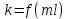
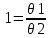
1 – m = 2; 2 – m = 3; 3 – m = 4;
При трех или четырех слагаемых в качестве q1 принимается составляющая, по числовому значению наиболее отличающаяся от других, в качестве q2 следует принять ближайшую к q1 составляющую.
Задача 1. Проверьте гипотезу об отсутствии ухода систематической погрешности (оцените, не происходит ли изменений в показаниях прибора). Уровень значимости α = 0,05%.
Решение. Предположим, что случайная величина срока безотказной работы подчинена нормальному закону распределения. Требуется проверить гипотезу о числовом значении математического ожидания нормально распределенной величины (генеральной средней) при неизвестной генеральной дисперсии. В этом случае в качестве критерия выбирают функцию
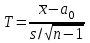,где
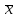– выборочная средняя, а0 – математическое ожидание, s – выборочное среднее квадратичное отклонение. Случайная величина Т имеет t-распределение (распределение Стьюдента) с 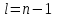степенями свободы.Требуется найти критическую область для нулевой гипотезы Н0: а0=0,05 при альтернативной гипотезе Н1: а1<2900. Очевидно, что другие альтернативные гипотезы (
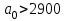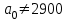и ) нецелесообразны, т.к. потребитель обычно обеспокоен лишь тем, что срок службы изделия может оказаться меньше гарантируемого поставщиком.Критическая область левосторонняя;
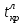находим из условия 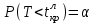.Задача 2. Определите, имеются ли грубые погрешности (выбросы) среди результатов многократных измерений, указанных в задаче № 1, при доверительной вероятности Р = 0,95 (95%), используя Критерий Граббса.
Расчеты выполнить с использованием Microsoft Office Excel
Решение
Следует проверить, является ли эта погрешность систематической.
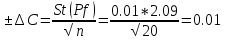
С -доверительный интервал концентраций.
S - стандартное отклонение, рассчитанное из 20 параллельных измерений концентрации
f - коэффициент Стъюдента, при Р=0,95, n=20
Разность среднего результата анализа и паспортного значения концентрации стандартного образца, взятого для исследования, больше доверительного интервала. Следовательно, методика отягощена систематической погрешностью.
Задача 3. Для выборки, приведенной в задаче № 1 с учетом удаления выбросов, определите случайную погрешность результатов измерений при доверительной вероятности Р = 0,95.
Расчеты выполнить с использованием Microsoft Office Excel
Представить методику расчета
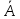, S, 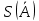, 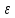и выбор t - коэффициент СтьюдентаРешение
Доверительные границы случайной погрешности вычисляются при доверительной вероятности P = 0,95, а также при P = 0,99, если измерения в дальнейшем повторить нельзя:
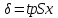
где tp – коэффициент Стьюдента, определяемый по табл. П.4 при заданной доверительной вероятности P и числе степеней свободы k. Для прямых измерений
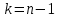
Границы неисключенной систематической погрешности
В качестве составляющих неисключенной систематической погрешности рассматриваются погрешности метода, погрешности средств измерений (например, пределы допускаемой основной и дополнительных погрешностей, если их случайные составляющие пренебрежимо малы) и погрешности, вызванные другими источниками. При суммировании составляющих неисключенные систематические погрешности средств измерений рассматриваются как случайные величины. Если их распределение неизвестно, то принимается равномерное распределение, и тогда границы неисключенной систематической погрешности результата при числе составляющих m > 4 определяют как
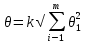
где
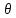– границы отдельных составляющих общим числом m;k – коэффициент, равный 1,1 при доверительной вероятности P = 0,95 и 1,4 при P = 0,99. Если же число суммируемых погрешностей m £ 4, то коэффициент k определяется по графику
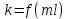
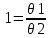
1 – m = 2; 2 – m = 3; 3 – m = 4;
При трех или четырех слагаемых в качестве q1 принимается составляющая, по числовому значению наиболее отличающаяся от других, в качестве q2 следует принять ближайшую к q1 составляющую.