Файл: 0 с объемной плотностью заряда, зависящей от координаты точки.docx
Добавлен: 26.10.2023
Просмотров: 32
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
М
 ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение
высшего образования
«Тольяттинский государственный университет»
Институт инженерной и экологической безопасности
(наименование института полностью)
Кафедра /департамент /центр __________________________________________________
(наименование кафедры/департамента/центра полностью)
ПРАКТИЧЕСКОЕ ЗАДАНИЕ №1
по дисциплине (учебному курсу) «Физика 2»
(наименование дисциплины (учебного курса)
Вариант 16
| Студент | Шорин Думан Жасуланович (И.О. Фамилия) | |
| Группа | ТБбд-2102а | |
| Преподаватель | Мелешко Игорь Вениаминович (И.О. Фамилия) | |
Тольятти 2023
Задача 1
Э
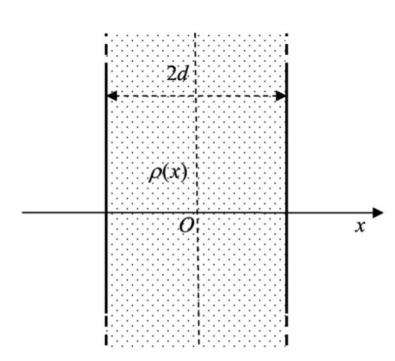 лектрический заряд распределен в пространственном слое между двумя параллельными бесконечными плоскостями симметрично относительно центральной плоскости x = 0 с объемной плотностью заряда
лектрический заряд распределен в пространственном слое между двумя параллельными бесконечными плоскостями симметрично относительно центральной плоскости x = 0 с объемной плотностью заряда 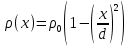 , зависящей от координаты
, зависящей от координаты 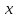 точки. Ось Xперпендикулярна слою. Толщина слоя 2d. Найти с помощью теоремы Гаусса зависимость проекции Ex на ось Xвектора напряженности электрического поля от координаты точки x. Построить график этой зависимости Ex(x) в интервале изменения координаты xот – 2dдо 2d.
точки. Ось Xперпендикулярна слою. Толщина слоя 2d. Найти с помощью теоремы Гаусса зависимость проекции Ex на ось Xвектора напряженности электрического поля от координаты точки x. Построить график этой зависимости Ex(x) в интервале изменения координаты xот – 2dдо 2d.| Дано: 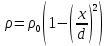 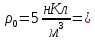 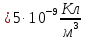 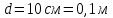 | 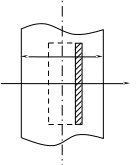 Решение: Решение:По теореме Гаусса: 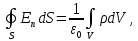 так как плоскости, ограничивающие слой бесконечны, то в силу симметрии так как плоскости, ограничивающие слой бесконечны, то в силу симметрии 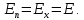 Выберем замкнутую поверхность в виде цилиндра с основанием 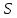 и высотой и высотой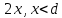 , тогда , тогда 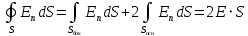 Так как 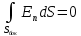 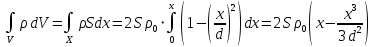 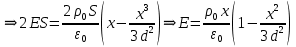 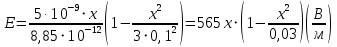 . .При 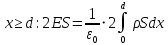 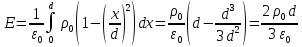 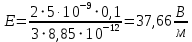 . .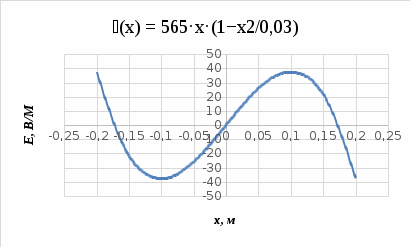 |
Задача 2
Н
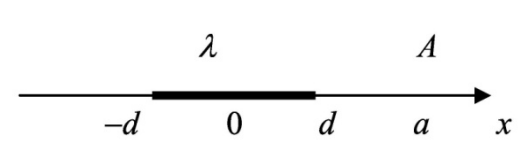 айти потенциал электростатического поля, создаваемого отрезком прямой длиной
айти потенциал электростатического поля, создаваемого отрезком прямой длиной 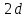 в точке A. Отрезок равномерно заряжен с линейной плотностью заряда
в точке A. Отрезок равномерно заряжен с линейной плотностью заряда 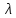 .
. Точка A лежит на оси
 , направленной вдоль отрезка, на расстоянии a от его середины.
, направленной вдоль отрезка, на расстоянии a от его середины.| Дано: 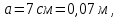 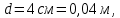 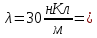 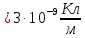 | Решение: 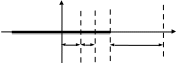 Выделим на проводнике элементарный отрезок длины 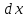 , несущий заряд , несущий заряд 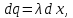 где где 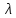 - линейная плотность заряда. Этот точечный заряд создает электрическое поле, потенциал которого в заданной точке A, равен - линейная плотность заряда. Этот точечный заряд создает электрическое поле, потенциал которого в заданной точке A, равен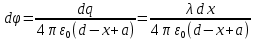 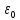 – электрическая постоянная – электрическая постоянная 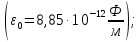 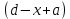 – расстояние от точки А до элемента – расстояние от точки А до элемента 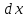 . .Интегрируя это выражение в пределах от 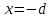 до до 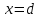 получим результирующий потенциал поля всего проводника: получим результирующий потенциал поля всего проводника: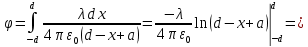 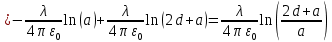 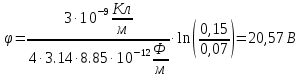 Ответ: 20,57 В. |
Задача 3
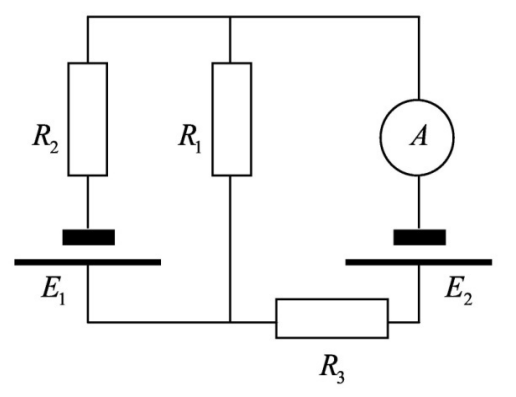
В схеме, приведенной на рисунке, ЭДС источников
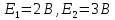 , сопротивления резисторов
, сопротивления резисторов 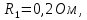
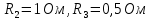 , сопротивление амперметра равно
, сопротивление амперметра равно 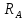 . Найти показание амперметра. Внутренним сопротивлением источников пренебречь.
. Найти показание амперметра. Внутренним сопротивлением источников пренебречь.| Дано: 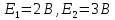 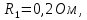 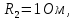 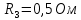 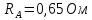 | Решение: Выберем произвольное направление токов.     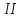 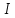 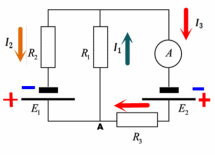 По первому правилу Кирхгофа алгебраическая сумма токов, сходящихся в одном узле, равна нулю: 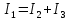 По второму правилу Кирхгофа для замкнутой цепи 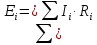 Второе правило Кирхгофа для контура I 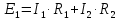 Выразим и подстваим сюда 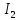 через через 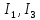 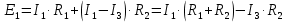 Второе правило Кирхгофа для контура II 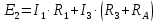 Исключим 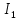 . Для этого умножим предпоследнее равенство на . Для этого умножим предпоследнее равенство на 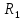 а последнее на а последнее на 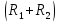 и вычтем результаты друг из друга. и вычтем результаты друг из друга.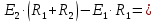 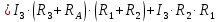 Отсюда получаем: 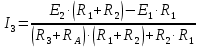 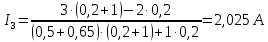 Ответ: 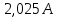 . . |