Файл: Методические указания по выполнению контрольной работы по учебной дисциплине ен. 02 Элементы математической логики.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 200
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
}.
На основе понятий пересечения и объединения двух множеств можно ввести аналогичные операции над несколькими множествами:
A1… An = (…((A1A2) A3) …) An ,
A1… An = (…((A1A2) A3) …) An .
III.Если А, В – множества, то существует множество А \ В – разность множеств А и В, которое состоит из всех элементов, принадлежащих множеству А, но не принадлежащих множеству В: x A \ B x A и x B.
Примеры:
1. Если A = {1, 2, 5, }, B = {{1}, 2, 5, }, то А\ В= {1}.
2. Если A = {x R | 1 < x 5}, B = {x R | –1 x < 2},
то A \ B ={ [2; 5]}.
IV. Если А – множество, то существует множество всех егоподмножествB(A), называемое также булеаном множества А, и состоящее из всех подмножеств множестваА: X B(A) X A.
Важно отметить, что булеан B(A) состоит из множеств (подмножество множества А само является множеством) и содержит в качестве элементов пустое множество и само множество А(которые в случае А= совпадают).
Примеры:
1. Если А= , то B(A) = {}.
2. Если A = {1}, то B(А) = {, {1}}.
3. Если A = {1, 2}, то B(А) = {, {1}, {2}, {1, 2}}.
4. Если A = {1, 2, 3}, то B(А) = {, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}.
Можно доказать, что булеан n-элементного множества Асостоит из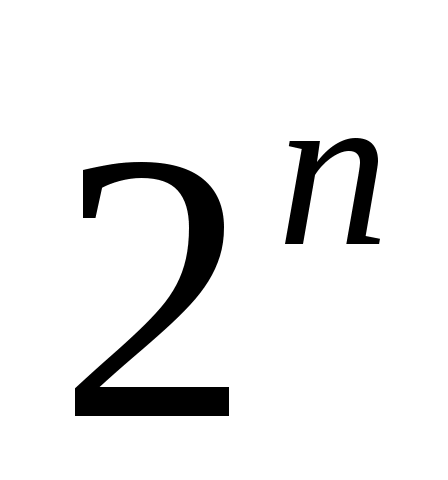 элементов. Поэтому булеан часто называют степенью множества Аи обозначают
элементов. Поэтому булеан часто называют степенью множества Аи обозначают 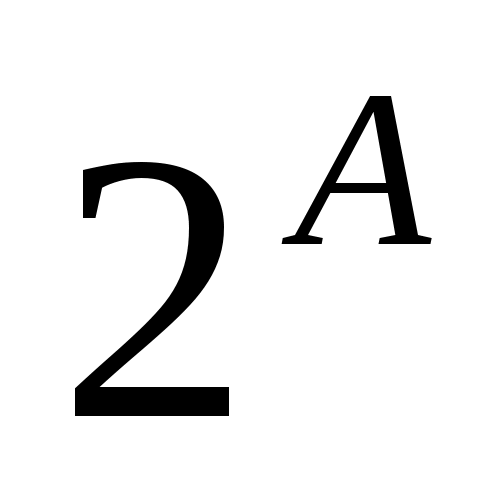 .
.
V. Если А, В – множества, то существует их прямое (декартово) произведение
АВ, состоящее из всех упорядоченных пар(a; b), гдеаА, b B:
АВ= {(a; b) | a A ,b B}.
Примеры:
1. Если А= {1}, B = {0, 5}, то АВ= {(1; 0), (1; 5)}.
2. Если А= {0, 2}, B = {0, 5}, то АВ= {(0; 0), (0; 5), (2; 0), (2; 5)}.
3. Если множество Асостоит из m элементов, а множество
В– из n элементов, то можно доказать, что множество АВсостоит из mn элементов. По этой причине в названии множества АВиспользуется термин “произведение”. Если А= B, то множество ААсостоит из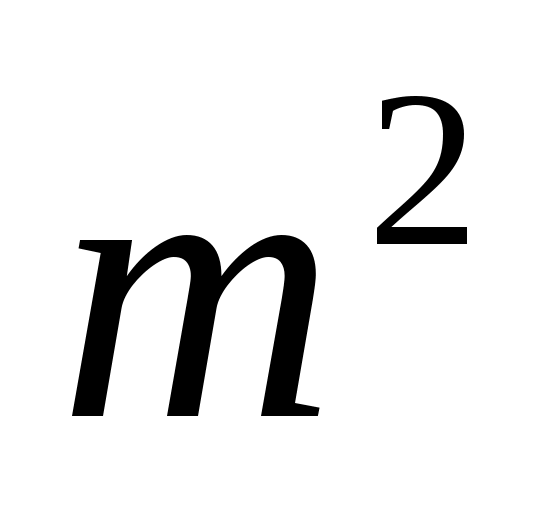 элементов и называется декартовымквадратом множестваАи обозначается через
элементов и называется декартовымквадратом множестваАи обозначается через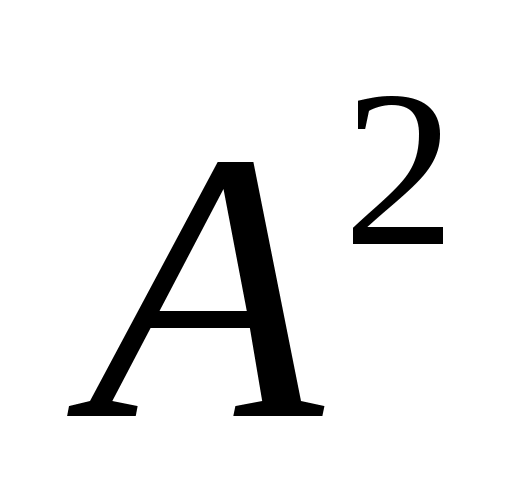 .
.
Вслед за декартовым произведением двух можно ввести и декартово произведение
A1 … An = ( … ((A1 A2) A3)…)An) n множествA1 , … , An . Множество A...A, состоящее из n множителей А называется декартовой степенью множества A и обозначается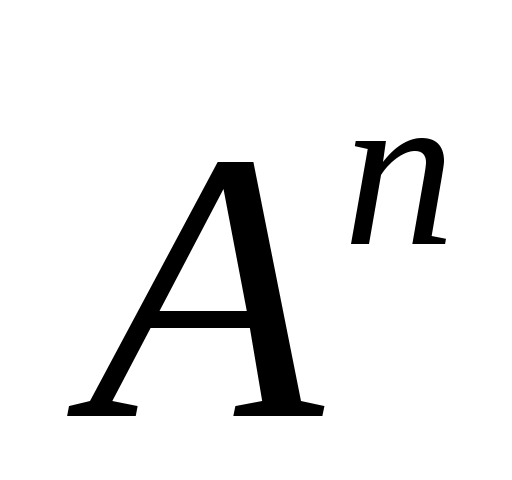 .
.
Декартово произведение АВ= {(a; b) | a A b B} двух множеств Аи Виногда условно изображают на плоскости, трактуя компоненты упорядоченной пары (a; b) как координаты: a – координата по оси x, на которой отмечают множество А, а b – координата по оси y, на которой отмечают множество В. Таким образом, элементы (a; b) АB условно изображаются точками на плоскости с “координатами” a и b.
Особенно удобно графическое изображение декартова произведения АВ в случае, когда Аи В–числовые множества, т.е. АR, B R . Тогда изображение принимает не условный характер, а имеет вполне конкретный геометрический смысл: множество АВпредставляет из себя множество точек M(a; b) декартовой плоскости, первая координата а которых принадлежит множеству А, а вторая b – принадлежит множеству В.
ЛОГИКА ВЫСКАЗЫВАНИЙ
1.Понятие высказывания. Операции над высказываниями
Под высказыванием понимают повествовательное предложение, которое может быть либо истинным, либо ложным.
Примеры:
1. «Волга впадает в Каспийское море»‖ - истинное высказывание.
2. «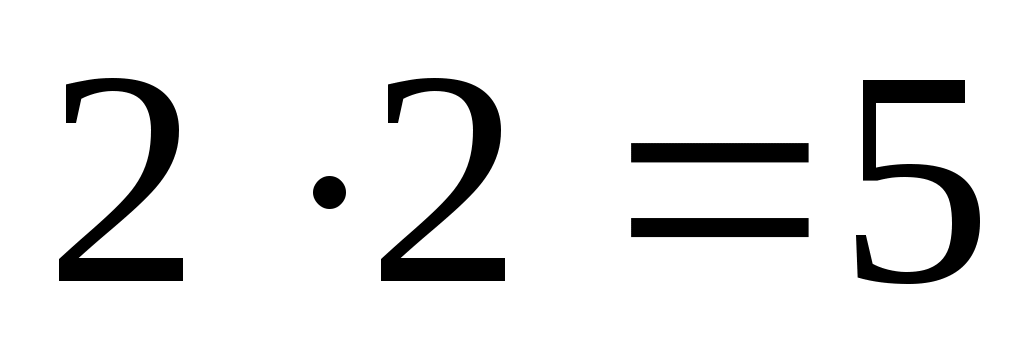 » - ложное высказывание.
» - ложное высказывание.
3. «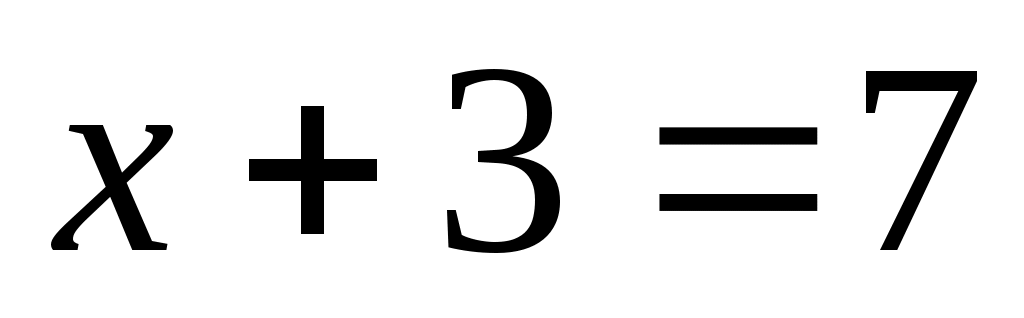 » - не является высказыванием, т.к. истинность этого равенства
» - не является высказыванием, т.к. истинность этого равенства
зависит от значения Х.
4. «Давайте, разберемся!» - не является высказыванием.
Высказывания обозначаются большими латинскими буквами А, В, C,… Подобно тому, как из заданных чисел можно получить другие числа с помощью операций сложения, вычитания, умножения и деления, так из заданных высказываний получаются новые с помощью операций, имеющих специальные названия: конъюнкция, дизъюнкция, импликация, эквивалентность и отрицание. Эти операции означают соединение отдельных предложений связками «и», «или», «если…,то…», «тогда и только тогда, когда…» и присоединение к высказыванию частицы «не».
Конъюнкция высказываний.
Конъюнкцией высказываний А и В называют новое высказывание, обозначаемое А˄В (читается «А и В»), которое истинно лишь в единственном случае, когда оба высказывания А и В истинны, и ложно во всех остальных случаях. Обозначим истинное высказывание – 1, а ложное - 0. В таблице 1 указаны значения истинности конъюнкции высказываний А и В.
Таблица 1 – Таблица истинности конъюнкции высказываний
Примеры:
1. Даны высказывания:
А: «Число 2- четное» – истинное высказывание
В: «Число 2-простое» – истинное высказывание
Тогда А˄В: «Число 2-четное и простое» – истинное высказывание
2. Даны высказывания:
А: « 3<12» – истинное высказывание
В: «12<10» – ложное высказывание
Тогда А˄В: «3<12<10» – ложное высказывание
Дизъюнкция высказывания.
Дизъюнкцией высказываний А и В называют новое высказывание, обозначаемое А В (читается «А или В»), которое ложно лишь в одном случае, когда оба высказывания А и В ложны, и истинно во всех остальных случаях.
В (читается «А или В»), которое ложно лишь в одном случае, когда оба высказывания А и В ложны, и истинно во всех остальных случаях.
В таблице 2 указаны значения истинности дизъюнкции высказываний А и В.
Таблица 2 - Таблица истинности дизъюнкции высказываний
Примеры:
1. Даны высказывания:
А: «22 двузначное число» – истинное высказывание
В: «22 нечетное число» – ложное высказывание
Тогда А В: «22 двузначное или нечетное число» - истинное высказывание
В: «22 двузначное или нечетное число» - истинное высказывание
2. Дано А В: «3≤3» - истинное высказывание
В: «3≤3» - истинное высказывание
Тогда А: «3<3» ложное высказывание, В: «3=3» – истинное высказывание.
Вывод: Дизъюнкция нескольких высказываний истинна, если истинно хотя бы одно из этих высказываний.
Импликация высказываний.
Импликацией высказываний А и В называют новое высказывание, обозначаемое А В
В
(читается «если А, то В»), которое ложное лишь в одном случае, когда А - истинно, а В - ложно.
В таблице 3 указаны значения истинности импликации высказываний А и В.
Таблица 3 - Таблица истинности импликации высказываний
Пример:
1. Даны высказывания:
А: «Последняя цифра числа 15 равна 5» - истинное высказывание
В: «Число 15 делится на 5» - истинное высказывание.
Тогда А→В: «Если последняя цифра числа 15 равна 5, то число 15 делится
на 5» - истинное высказывание.
Эквивалентность высказываний.
Эквивалентностью высказываний А и В называют новое высказывание, обозначаемое А↔В (читается «А тогда и только тогда, когда В»), которое истинно в том и только том случае, когда одновременно оба высказывания А и В либо истинны, либо ложны, а во всех остальных случаях – ложно.
В таблице 4 указаны значения истинности эквивалентности высказываний А и В
Таблица 4 - Таблица истинности эквивалентности высказываний
Отрицание высказываний.
Отрицанием высказывания А называют новое высказывание обозначаемое
На основе понятий пересечения и объединения двух множеств можно ввести аналогичные операции над несколькими множествами:
A1… An = (…((A1A2) A3) …) An ,
A1… An = (…((A1A2) A3) …) An .
III.Если А, В – множества, то существует множество А \ В – разность множеств А и В, которое состоит из всех элементов, принадлежащих множеству А, но не принадлежащих множеству В: x A \ B x A и x B.
Примеры:
1. Если A = {1, 2, 5, }, B = {{1}, 2, 5, }, то А\ В= {1}.
2. Если A = {x R | 1 < x 5}, B = {x R | –1 x < 2},
то A \ B ={ [2; 5]}.
IV. Если А – множество, то существует множество всех егоподмножествB(A), называемое также булеаном множества А, и состоящее из всех подмножеств множестваА: X B(A) X A.
Важно отметить, что булеан B(A) состоит из множеств (подмножество множества А само является множеством) и содержит в качестве элементов пустое множество и само множество А(которые в случае А= совпадают).
Примеры:
1. Если А= , то B(A) = {}.
2. Если A = {1}, то B(А) = {, {1}}.
3. Если A = {1, 2}, то B(А) = {, {1}, {2}, {1, 2}}.
4. Если A = {1, 2, 3}, то B(А) = {, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}.
Можно доказать, что булеан n-элементного множества Асостоит из
V. Если А, В – множества, то существует их прямое (декартово) произведение
АВ, состоящее из всех упорядоченных пар(a; b), гдеаА, b B:
АВ= {(a; b) | a A ,b B}.
Примеры:
1. Если А= {1}, B = {0, 5}, то АВ= {(1; 0), (1; 5)}.
2. Если А= {0, 2}, B = {0, 5}, то АВ= {(0; 0), (0; 5), (2; 0), (2; 5)}.
3. Если множество Асостоит из m элементов, а множество
В– из n элементов, то можно доказать, что множество АВсостоит из mn элементов. По этой причине в названии множества АВиспользуется термин “произведение”. Если А= B, то множество ААсостоит из
Вслед за декартовым произведением двух можно ввести и декартово произведение
A1 … An = ( … ((A1 A2) A3)…)An) n множествA1 , … , An . Множество A...A, состоящее из n множителей А называется декартовой степенью множества A и обозначается
Декартово произведение АВ= {(a; b) | a A b B} двух множеств Аи Виногда условно изображают на плоскости, трактуя компоненты упорядоченной пары (a; b) как координаты: a – координата по оси x, на которой отмечают множество А, а b – координата по оси y, на которой отмечают множество В. Таким образом, элементы (a; b) АB условно изображаются точками на плоскости с “координатами” a и b.
Особенно удобно графическое изображение декартова произведения АВ в случае, когда Аи В–числовые множества, т.е. АR, B R . Тогда изображение принимает не условный характер, а имеет вполне конкретный геометрический смысл: множество АВпредставляет из себя множество точек M(a; b) декартовой плоскости, первая координата а которых принадлежит множеству А, а вторая b – принадлежит множеству В.
ЛОГИКА ВЫСКАЗЫВАНИЙ
1.Понятие высказывания. Операции над высказываниями
Под высказыванием понимают повествовательное предложение, которое может быть либо истинным, либо ложным.
Примеры:
1. «Волга впадает в Каспийское море»‖ - истинное высказывание.
2. «
3. «
зависит от значения Х.
4. «Давайте, разберемся!» - не является высказыванием.
Высказывания обозначаются большими латинскими буквами А, В, C,… Подобно тому, как из заданных чисел можно получить другие числа с помощью операций сложения, вычитания, умножения и деления, так из заданных высказываний получаются новые с помощью операций, имеющих специальные названия: конъюнкция, дизъюнкция, импликация, эквивалентность и отрицание. Эти операции означают соединение отдельных предложений связками «и», «или», «если…,то…», «тогда и только тогда, когда…» и присоединение к высказыванию частицы «не».
Конъюнкция высказываний.
Конъюнкцией высказываний А и В называют новое высказывание, обозначаемое А˄В (читается «А и В»), которое истинно лишь в единственном случае, когда оба высказывания А и В истинны, и ложно во всех остальных случаях. Обозначим истинное высказывание – 1, а ложное - 0. В таблице 1 указаны значения истинности конъюнкции высказываний А и В.
Таблица 1 – Таблица истинности конъюнкции высказываний
-
А
В
А˄В
0
0
0
0
1
0
1
0
0
1
1
1
Примеры:
1. Даны высказывания:
А: «Число 2- четное» – истинное высказывание
В: «Число 2-простое» – истинное высказывание
Тогда А˄В: «Число 2-четное и простое» – истинное высказывание
2. Даны высказывания:
А: « 3<12» – истинное высказывание
В: «12<10» – ложное высказывание
Тогда А˄В: «3<12<10» – ложное высказывание
Дизъюнкция высказывания.
Дизъюнкцией высказываний А и В называют новое высказывание, обозначаемое А
В таблице 2 указаны значения истинности дизъюнкции высказываний А и В.
Таблица 2 - Таблица истинности дизъюнкции высказываний
| А | В | А |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Примеры:
1. Даны высказывания:
А: «22 двузначное число» – истинное высказывание
В: «22 нечетное число» – ложное высказывание
Тогда А
2. Дано А
Тогда А: «3<3» ложное высказывание, В: «3=3» – истинное высказывание.
Вывод: Дизъюнкция нескольких высказываний истинна, если истинно хотя бы одно из этих высказываний.
Импликация высказываний.
Импликацией высказываний А и В называют новое высказывание, обозначаемое А
(читается «если А, то В»), которое ложное лишь в одном случае, когда А - истинно, а В - ложно.
В таблице 3 указаны значения истинности импликации высказываний А и В.
Таблица 3 - Таблица истинности импликации высказываний
-
А
В
А В
В
0
0
1
0
1
1
1
0
0
1
1
1
Пример:
1. Даны высказывания:
А: «Последняя цифра числа 15 равна 5» - истинное высказывание
В: «Число 15 делится на 5» - истинное высказывание.
Тогда А→В: «Если последняя цифра числа 15 равна 5, то число 15 делится
на 5» - истинное высказывание.
Эквивалентность высказываний.
Эквивалентностью высказываний А и В называют новое высказывание, обозначаемое А↔В (читается «А тогда и только тогда, когда В»), которое истинно в том и только том случае, когда одновременно оба высказывания А и В либо истинны, либо ложны, а во всех остальных случаях – ложно.
В таблице 4 указаны значения истинности эквивалентности высказываний А и В
Таблица 4 - Таблица истинности эквивалентности высказываний
-
А
В
А↔В
0
0
1
0
1
0
1
0
0
1
1
1
Отрицание высказываний.
Отрицанием высказывания А называют новое высказывание обозначаемое