Файл: Контрольная работа по дисциплине Математика Семестр 1 Вариант 5 студент гр. Иб750621 Волкова Дарья.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 52
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Тульский государственный университет»
Интернет-институт
КОНТРОЛЬНАЯ РАБОТА
по дисциплине
«Математика»
Семестр 1
Вариант 5
Выполнил: студент гр. ИБ750621
Волкова Дарья
Проверил: д.ф.-м.н., проф. Христич Д.В.
Тула, 2023
Задание 1. Для определителя∆ =
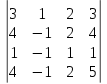 найти дополнительный минор элемента α13.
найти дополнительный минор элемента α13.Решение:
-
Сперва запишем минор α13, а потом вычислим его значение. Для того, чтобы составить α13 , вычеркнем из матрицы первую строку и третий столбец (именно на пересечении первой строки и третьего столбца расположен элемент α13). Мы получим новую матрицу, определитель которой и есть искомый минор α13:
α13=
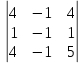
-
Вычисляем минор: α13=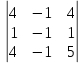 = 4*(-1)*5+(-1)*1*4+1*(-1)*4-4*(-1)*4-(-1)*1*5-5*1*(-1)= -3
= 4*(-1)*5+(-1)*1*4+1*(-1)*4-4*(-1)*4-(-1)*1*5-5*1*(-1)= -3
минор элемента α13= - 3
Задание 2. Найти матрицы [АВ], [ВА], [
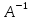 ], если
], если 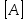 =
=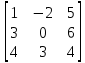 ,
, 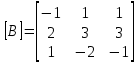
Решение:
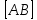 Компоненты матрицы С вычисляются следующим образом:
Компоненты матрицы С вычисляются следующим образом:-
c11 = a11 * b11 + a12 * b21 + a13 * b31 =1*(-1) + (-2)*2 + 5*1=(-1) - 4 + 5=0
c12 = a11 *b12 + a12 *b22 + a13 * b32 =1*1 + (-2)*3 + 5*(-2)=1 - 6 - 10=-15
c13 = a11 * b13 + a12 * b23 + a13 *b33 =1*1 + (-2)*3 + 5*(-1)=1 - 6 - 5=-10
c21 = a21 * b11 + a22 * b21 + a23 * b31 =3*(-1) + 0*2 + 6*1=(-3) + 0 + 6=3
c22 = a21*b12 + a22 * b22 + a23 * b32 =3*1 + 0*3 + 6*(-2)=3 + 0 - 12=-9
c23 = a21 * b13 + a22 * b23 + a23 * b33 =3*1 + 0*3 + 6*(-1)=3 + 0 - 6=-3
c31 = a31 * b11 + a32* b21 + a33 * b31 =4*(-1) + 3*2 + 4*1=(-4) + 6 + 4=6
c32 = a31 * b12 + a32 * b22 + a33 * b32 =4*1 + 3*3 + 4*(-2)=4 + 9 - 8=5
c33 = a31 * b13 + a32 *b23 + a33 * b33 = 4 * 1 + 3* 3 + 4 * (-1) = 4 + 9 - 4 = 9
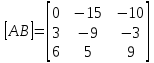
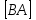 Компоненты матрицы С вычисляются следующим образом:
Компоненты матрицы С вычисляются следующим образом:c11 = a11 *b11 + a12 * b21 + a13 * b31 =1*(-1) + (-2)*2 + 5*1=(-1) - 4 + 5=0
c12 = a11 * b12 + a12 * b22 + a13 * b32 =1*1 + (-2)*3 + 5*(-2)=1 - 6 - 10=-15
c13 = a11 * b13 + a12 * b23 + a13 * b33 =1*1 + (-2)*3 + 5*(-1)=1 - 6 - 5=-10
c21 = a21 *b11 +a22 * b21 + a23 * b31 =3*(-1) + 0*2 + 6*1=(-3) + 0 + 6=3
c22 = a21 *b12 + a22 * b22 + a23 * b32 =3*1 + 0*3 + 6*(-2)=3 + 0 - 12=-9
c23 = a21 * b13 + a22 * b23 + a23 * b33 =3*1 + 0*3 + 6*(-1)=3 + 0 - 6=-3
c31 = a31 * b11 + a32 * b21 + a33 * b31 =4*(-1) + 3*2 + 4*1=(-4) + 6 + 4=6
c32 = a31 * b12 + a32 * b22 + a33 *b32 =4*1 + 3*3 + 4*(-2)=4 + 9 - 8=5
c33 = a31 * b13 + a32 * b23 + a33 * b33 = 4 *1 + 3 * 3 + 4 * (-1) = 4 + 9 - 4 = 9
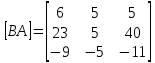
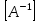 Для вычисления обратной матрицы запишем матрицу А, дописав к ней справа единичную матрицу:
Для вычисления обратной матрицы запишем матрицу А, дописав к ней справа единичную матрицу: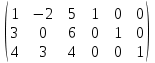
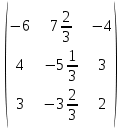
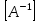 =
= 
Задание 3. Проверить совместность системы уравнений и в случае совместности решить ее по правилу Крамера
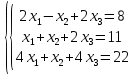
Решение:
-
∆ = =2
=2 -
∆1=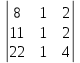 =6
=6 -
∆2 =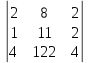 =-12
=-12 -
∆3 =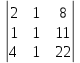 =20
=20 -
Х1=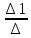 =
=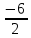 = -3;
= -3;
Х2 =
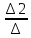 =
=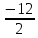 = -6;
= -6; Х3 =
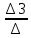
=
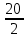 = 10;
= 10;Задача 4. Доказать, что векторы a b c образуют базис, и найти координаты вектора d в этом базисе: a 2,1,3,b 3,6,2, c 5,3,1, d 31,6,22.
Решение:
-
Вычислим определитель матрицы:
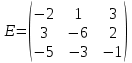
-
∆ = -2∙((-6)∙(-1) - (-3)∙2) - 3∙(1∙(-1) - (-3)∙3) + -5∙(1∙2 - (-6)∙3) = -148
Определитель матрицы равен ∆ = -148
-
Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор d можно разложить по данному базису. Т.е. существуют такие числа α1, α2, α3, что имеет место равенство:
d = α1ε1 + α2ε2 + α3ε3
-
Запишем данное равенство в координатной форме:
(31;-6;22) = α(-2;1;3) + α(3;-6;2) + α(-5;-3;-1)
-
Используя свойства векторов, получим следующее равенство:
(31;-6;22) = (-2α1;1α1;3α1;) + (3α2;-6α2;2α2;) + (-5α3;-3α3;-1α3;)
(31;-6;22) = (-2α1 + 3α2 -5α3;1α1 -6α2 -3α3;3α1 + 2α2 -1α3)
6)По свойству равенства векторов имеем:
-2α1 + 3α2 -5α3 = 31
1α1 -6α2 -3α3 = -6
3α1 + 2α2 -1α3 = 22
7)Решаем полученную систему уравнений методом Крамера.
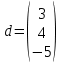
d= 3ε1 + 4ε2 -5ε3З
Задача 5. Вершины пирамиды находятся в точках А(5,2,4), В(−3,5,−7), С(1,−5,8), D(9,−3,5). Найти объем пирамиды и длину высоты, опущенной из вершины С.
Решение:
V=
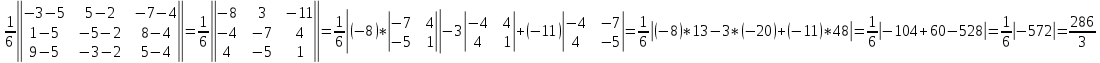
hc=
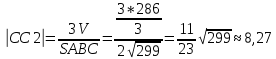
Задача 6.Найти расстояние от точки M0 до плоскости, проходящей через точки M1,M2,M3, если М1(-2,-1,-1) М2(0,3,2) М3(3,1,-4)М0(-21,20,-16)
Решение:
1)Найдем уравнение плоскости:
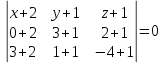
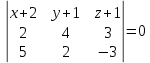
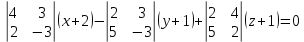
10(x+2)+21(y+1)-16(z+1)=0
10x+21y-16z=0
-
Расстояние от точки до плоскости:
P=
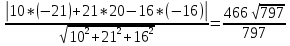
Задача 7.Написать канонические уравнения прямой 6x -5y - 4z +8 = 0, 6x + 5y + 3z + 4 = 0.
Решение:
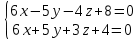
Любое решение системы: X=0:
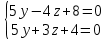 +
+-z+12=0
z=12
5y+36+4=0
y=8
Направляющий вектор прямой:
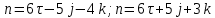
P=
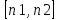 =
=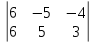 =
=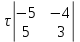 -j
-j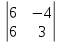 +k
+k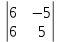 =5
=5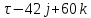
Каноническое уравнение:
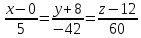
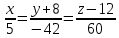
Задача 8. Найти точку пересечения прямой, заданной каноническими уравнениями, и плоскости
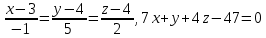
Решение:
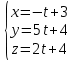
7(-t+3)+(5t+4)+4(2t+4)-47=0 t=1
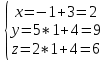
(2;9;6)
Задача 9. Вычислить предел
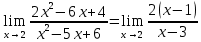 =
= 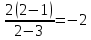
Задача 10. Вычислить предел
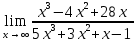 =
= 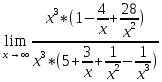 =
= 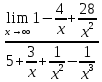 =
= 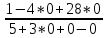 = 0,2
= 0,2Задача 11. Вычислить предел
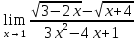 =
= 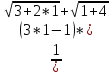 =
= 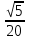
Задача 12. Вычислите предел
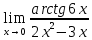 =
= 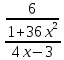 =
= 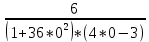 = -2
= -2Задача 13. Вычислите предел
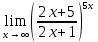
=
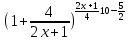 =
= 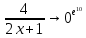 = е10
= е10Задача 14. Составить уравнение нормали к данной кривой в точке с абсциссой x0
Y=x+
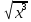 , x0=1
, x0=1-
Запишем уравнения касательной в общем виде:
yk = y0 + y'(x0)(x - x0)
По условию задачи x0 = 1, тогда y0 = 2 -
Теперь найдем производную: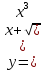 = 2,5
= 2,5 -
В результате имеем:
yk = y0 + y(x0)(x - x0)
ук=2+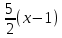
или
ук=5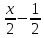
-
Запишем уравнения нормали в общем виде:
уn=y0-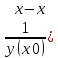 0)
0) -
В результате имеем:
yn=2-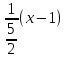
или
yn=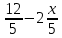
Задача 15. Найти дифференциал функции в точке с абсциссой х0
y=
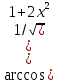 , x=0
, x=0y
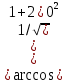 =
= 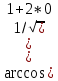 = y=
= y= 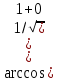 =
= 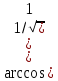 =
= 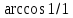 =
= 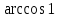 =0
=0