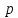ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 30
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рис.4.1.Схема задания
 =
=  = R = M*100 = 100 Ом
= R = M*100 = 100 ОмL= M*
 = 1*
= 1* = 1 мГн
= 1 мГнПереходим к схеме замещения цепи для комплексных действующих значений токов и напряжений :
R ->
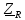 = R
= R L->
 =
= 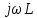
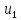 (t) - >
(t) - > 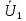 ;
; 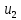 (t) - >
(t) - > 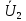
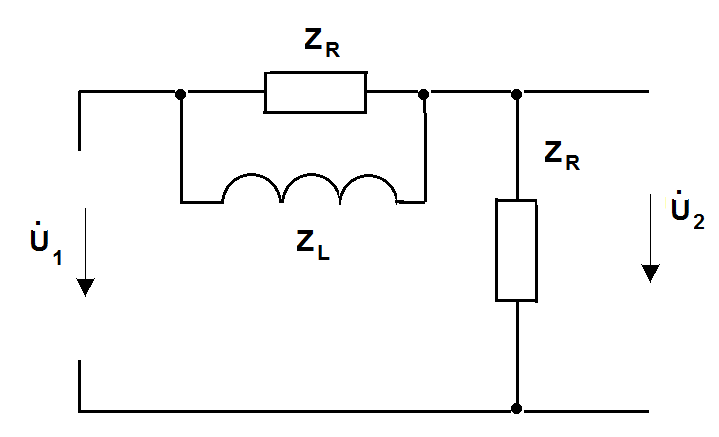
Рис.4.2.Схема замещения цепи для комплексных действующих значений токов и напряжений
Комплексное воздействие
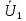
Комплексная реакция определяется по схеме делителя
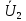 =
= 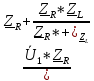 =
= 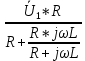 =
= 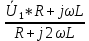
H(j
 ) =
) = 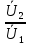 =
= 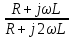
АЧХ = | H(j
 )| =
)| = 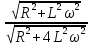
ФЧХ
Θ(ω) = arctg(
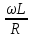 )
) - arctg(
- arctg(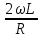 )
) H(j
 ) =
) = 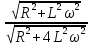 *
*
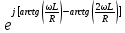
При
 = 0
= 0| H(j
 )| =
)| = 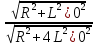 = 1
= 1Θ(ω) = arctg(
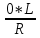 )
) - arctg(
- arctg(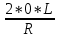 ) = 0
) = 0При
 = ∞
= ∞| H(j
 )| =
)| = 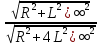 = 0,5
= 0,5Θ(ω) = arctg(
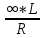 )
) - arctg(
- arctg(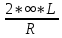 ) = 0
) = 0граничную частоту полосы пропускания
 определим при
определим при | H(j
 )| =
)| = 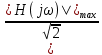 =
= 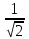
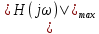 = 1
= 1| H(j
 )| =
)| = 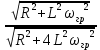 =
= 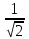
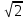 *
*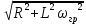 =
= 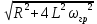
2*(
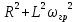 ) =
) = 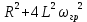
 =
= 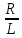 *
*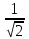
Θ(
 ) = arctg(
) = arctg(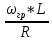 )
) - arctg(
- arctg(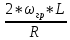
) = arctg(
 )
) - arctg(
- arctg(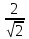 ) = - 19,5 ̊
) = - 19,5 ̊ 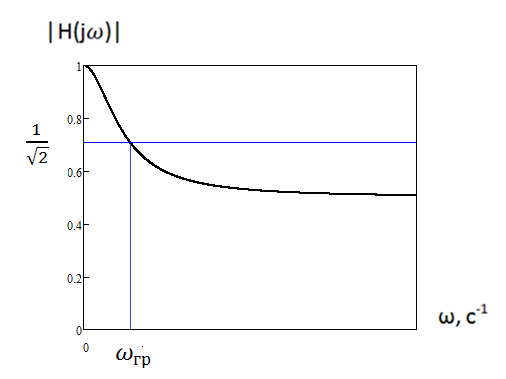
Рис.4.3.АЧХ
По графику АЧХ видно, что цепь пропускает нижние частоты в диапазоне 0 -

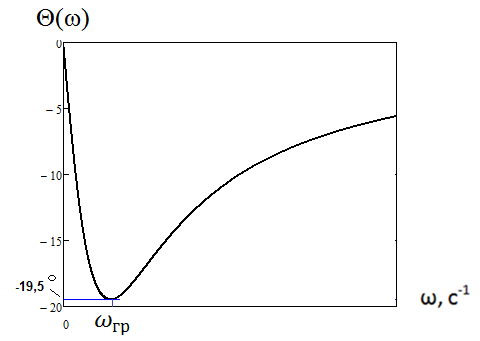
Рис.4.4.ФЧХ
Задача 5
Анализ переходных колебаний в электрической цепи классическим методом
Найдите закон изменения напряжения и тока на реактивном элементе
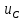 (t),
(t), 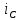 (t) после коммутации при условии, что до коммутации в цепи был установившийся режим.
(t) после коммутации при условии, что до коммутации в цепи был установившийся режим.Для этого:
1. Выберите для своего варианта схему цепи и рассчитайте её параметры через M и N из табл. 1.6, если последняя цифра номера зачётной книжки нечётная, или из табл. 1.7, если – чётная (цифру 0 считать чётной).
2. Составьте для схемы, получившейся после коммутации, систему уравнений по законам Кирхгофа для мгновенных значений токов и напряжений и получите одно дифференциальное уравнение относительно
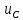 (t).
(t).3. Найдите путём решения полученного дифференциального уравнения искомую реакцию цепи
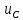 (t).по которой определите
(t).по которой определите 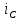 (t).соответственно.
(t).соответственно.4. Постройте графики функций
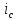 (t),
(t), 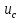 (t).
(t).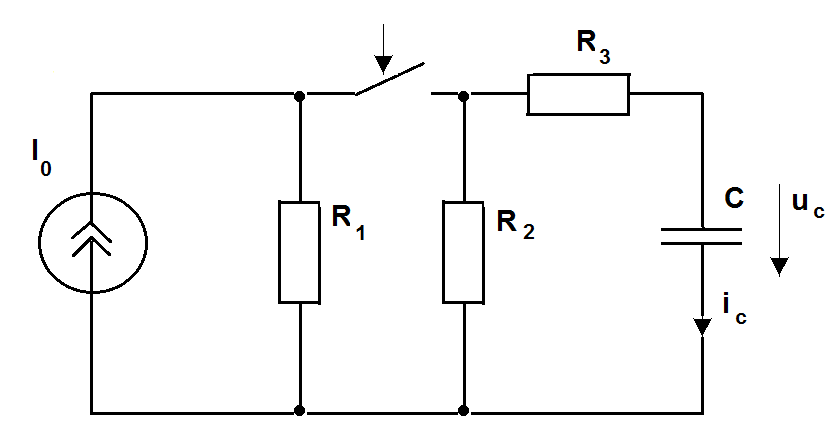
Рис.5.1.Схема задания
 =
=  = 2*(M+
= 2*(M+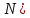 = 2*(1+5)= 12 Ом
= 2*(1+5)= 12 Ом = M+
= M+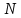 = 1 + 5= 6 Ом
= 1 + 5= 6 ОмC=
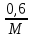
=
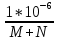 =
= 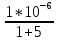 =
= 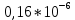 = 0,16 мкФ
= 0,16 мкФ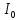 =
= 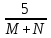 =
= 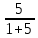 = 0,83 A
= 0,83 A1.Найдем начальные условия (t=0-).
Ток ёмкости в режиме постоянного тока равен нулю, что эквивалентно размыканию ветви с ёмкостью
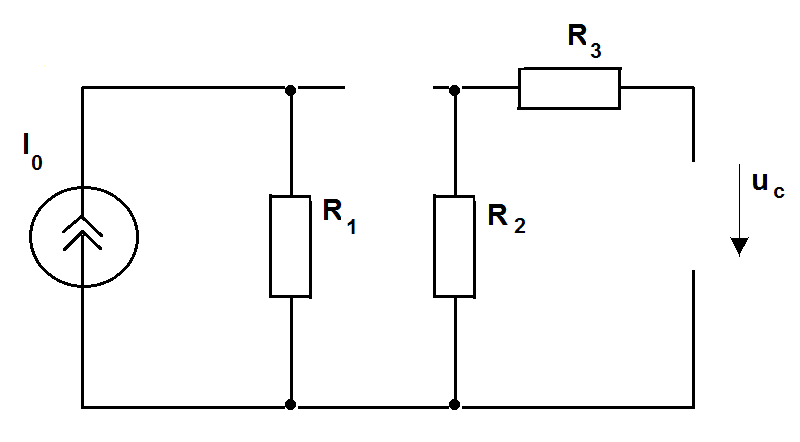
Рис.5.2.Схема определения начального условия.
 (0-)=
(0-)= 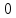
2. Составим дифференциальное уравнение цепи после коммутации относительно
 (t)
(t)
Рис.5.3.Схема расчёта переходного процесса после коммутации
Упростим схему
Замени параллельные
 и
и  эквивалентным
эквивалентным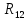 =
= 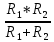
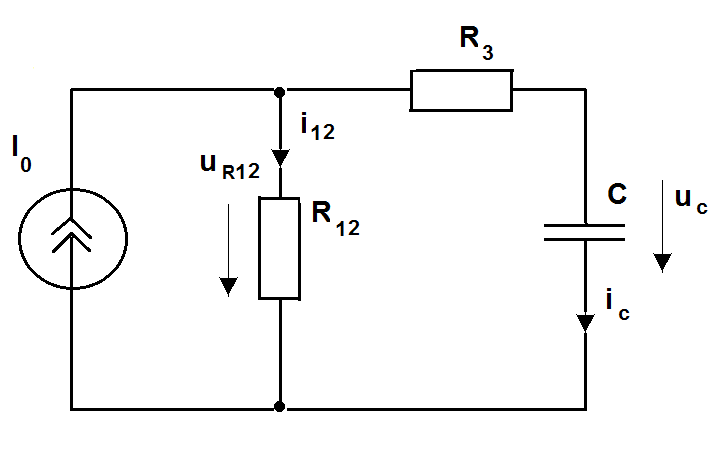
Рис.5.4.Преобразованная схема расчёта переходного процесса после коммутации
Уравнение по 1- му закону Кирхгофа
 -
-  -
-  = 0
= 0В то же время
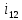 =
= 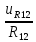 ;
;  = C*
= C*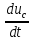 ;
; 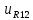 =
=
 *
* +
+  =
= 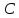 *
*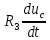 +
+ 
Подставим в 1-е уравнение
 -
- 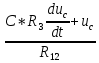 - C*
- C* = 0
= 0 Отсюда
 +
+ 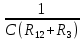 *
* =
= 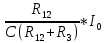
3. Общее решение полученного однородного дифференциального
уравнения имеет вид:
 (t) =
(t) = 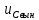 (t) +
(t) + 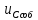 (t)
(t)4.Вынужденная составляющая (t->∞)
Ток ёмкости в режиме постоянного тока равен нулю, что эквивалентно размыканию ветви с ёмкостью
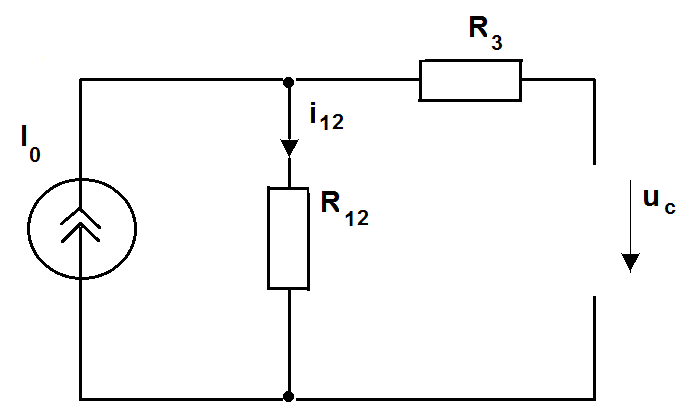
Рис.5.5.Схема определения вынужденной составляющей
По методу рычага
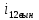 =
= 
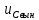 =
= 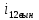 *
*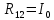 *
*
5. Определим собственную составляющую
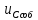 (t) = A*
(t) = A*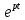
где – p -корень характеристического уравнения, соответствующий однородному дифференциальному уравнению
Корень получаем из однородного дифференциального уравнения путем замены производной на переменную р: