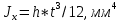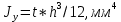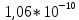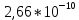Файл: Вити нияу мифи факультет кафедра направление подготовки лабораторная работа по дисциплине Сопротивление материалов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 12
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВОНАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«Национальный исследовательский ядерный университет «МИФИ»
Волгодонский инженерно-технический институт –
филиал федерального государственного автономного образовательного учреждения высшего образования
«Национальный исследовательский ядерный университет «МИФИ»
(ВИТИ НИЯУ МИФИ)
| ФАКУЛЬТЕТ | _ ___________ |
| КАФЕДРА | _ |
НАПРАВЛЕНИЕ ПОДГОТОВКИ _ ____
ЛАБОРАТОРНАЯ РАБОТА
ПО ДИСЦИПЛИНЕ: Сопротивление материалов .
РАБОТУ ВЫПОЛНИЛ СТУДЕНТ: _ _______
РАБОТУ ПРИНЯЛ ПРЕПОДАВАТЕЛЬ:.
Волгодонск
2023
| Кафедра МиПМ | Определение перемещений в консольной балке при косом изгибе | Лабораторная работа №1 | ||||||||||||||||||||||||||||||||||||||||||||||
| Цель работы: экспериментальное измерение перемещений в консольной упругой балке под действием изгибающих нагрузок, действующих не в плоскости основных осей инерции сечения, сравнение полученных результатов с расчетными значениями Оборудование и инструменты: экспериментальная установка «Косой изгиб балки» ТМ-КИБ-014, линейка, штангенциркуль. Отчет по работе Косой изгиб – изгиб, при котором силовая плоскость, не совпадает ни с одной из главных плоскостей инерции. Силовая плоскость – плоскость, в которой расположены внешние нагрузки. Главная плоскость инерции – плоскость, проходящая через геометрическую (продольную) ось бруса и одну из главных центральных осей инерции поперечного сечения. При нагружении консольной балки сосредоточенной силой, в ней возникает изгибающий момент, линейно распределенный по длине (рис. 1). 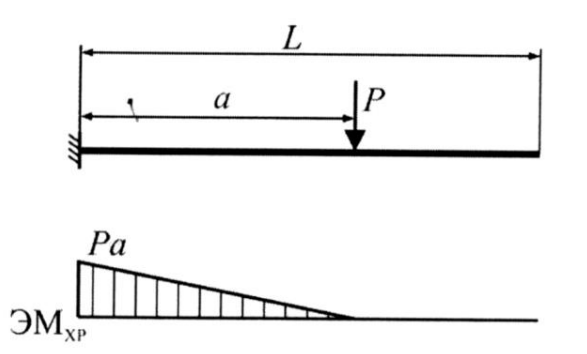 Рисунок 5.1 – Схема нагружения и эпюра изгибающего момента Mx=M*sin(α) My=M*cos(α) 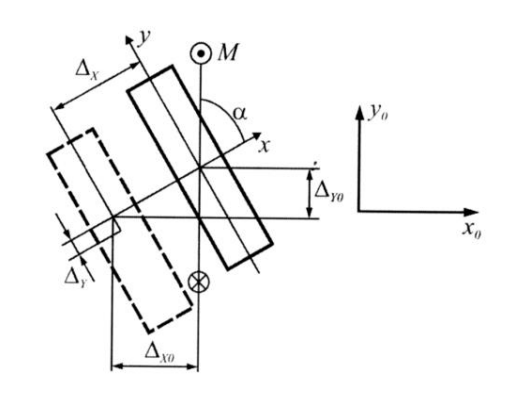 Рисунок 2 – Вводимые обозначения Значения перемещений в глобальных осях и в главных осях балки могут быть связаны следующим образом ΔX0=ΔX*sin(α) – Δy*cos(α) ΔX0=ΔX*cos(α) – Δy*sin(α) Перемещения балки при изгибе относительно ее главных осей могут быть вычислены с помощью интеграла Мора. Линейное перемещение в произвольной точке на расстоянии b от заделки определяется: 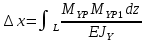 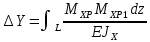 где – момент от единичной силы, приложенной в рассматриваемой точке в направлении главной оси Oх; – момент от единичной силы, приложенной в рассматриваемой точке в направлении главной оси Oy; Е – модуль упругости материала балки; – момент инерции сечения относительно оси Oх; – момент инерции сечения относительно оси Oy. Проведение испытаний и обработка опытных данных Таблица 1 – Геометрические параметры образца
Таблица 2 – Протокол испытаний
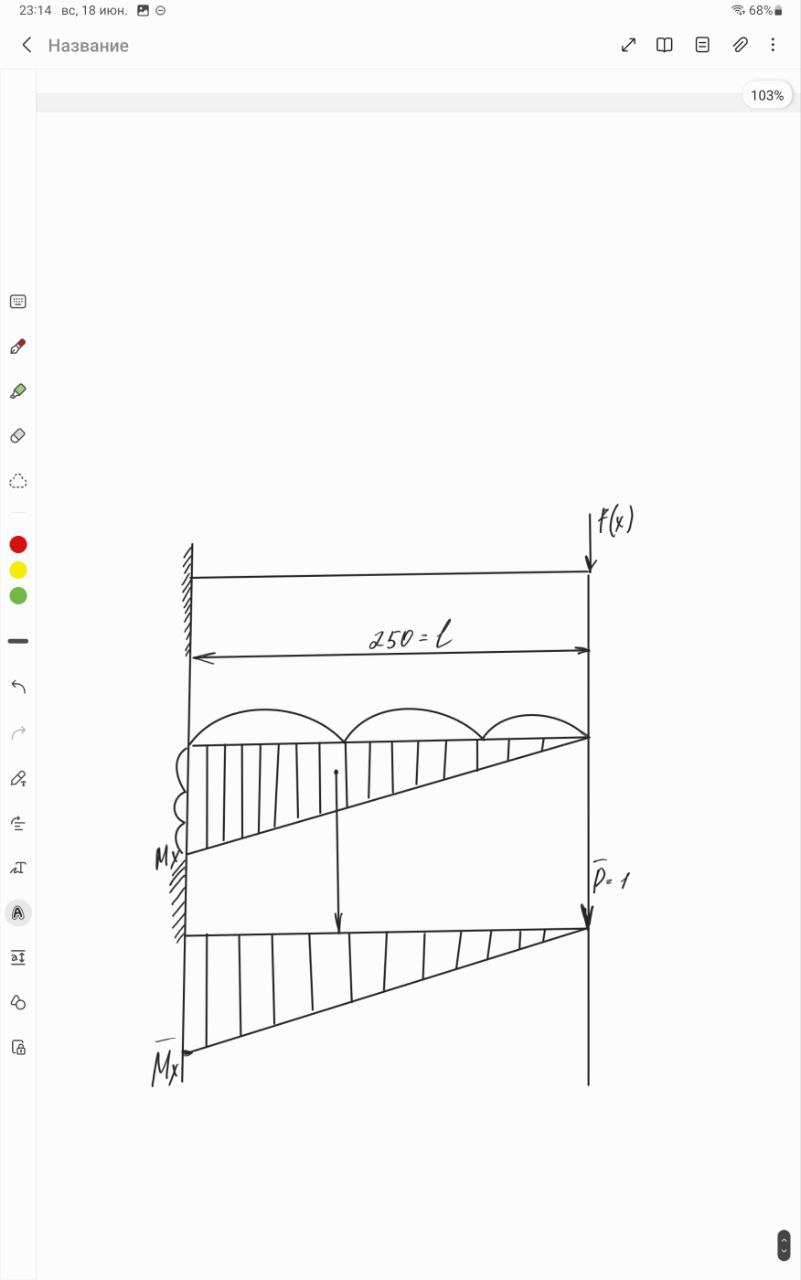 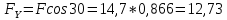 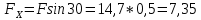 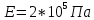 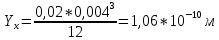 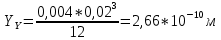 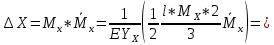 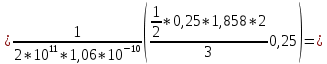 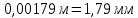 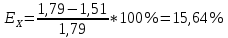 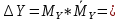 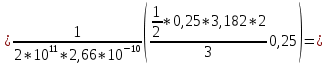 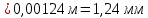 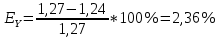 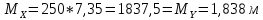 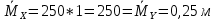 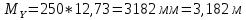 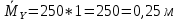 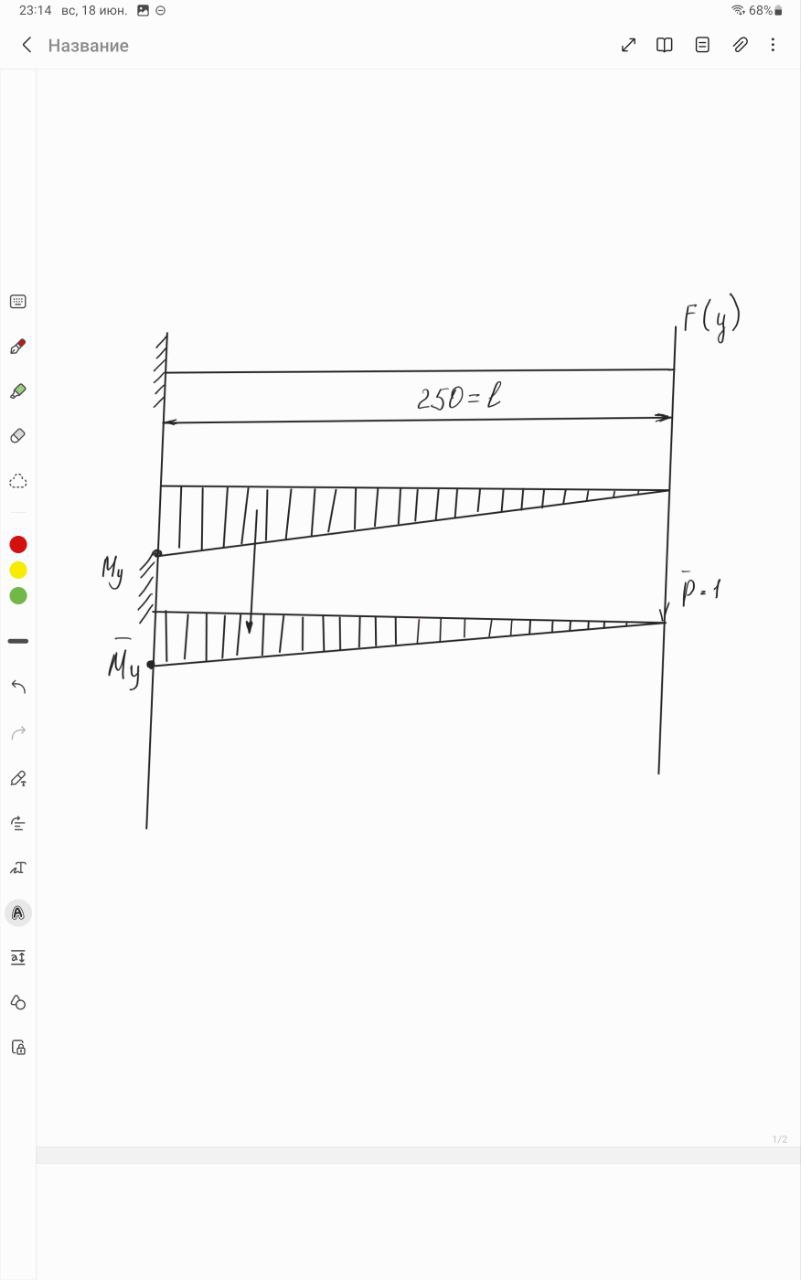 Вывод: В | ||||||||||||||||||||||||||||||||||||||||||||||||
| Работу выполнил студент | Работу проверил преподаватель | Подпись преподавателя и дата | ||||||||||||||||||||||||||||||||||||||||||||||