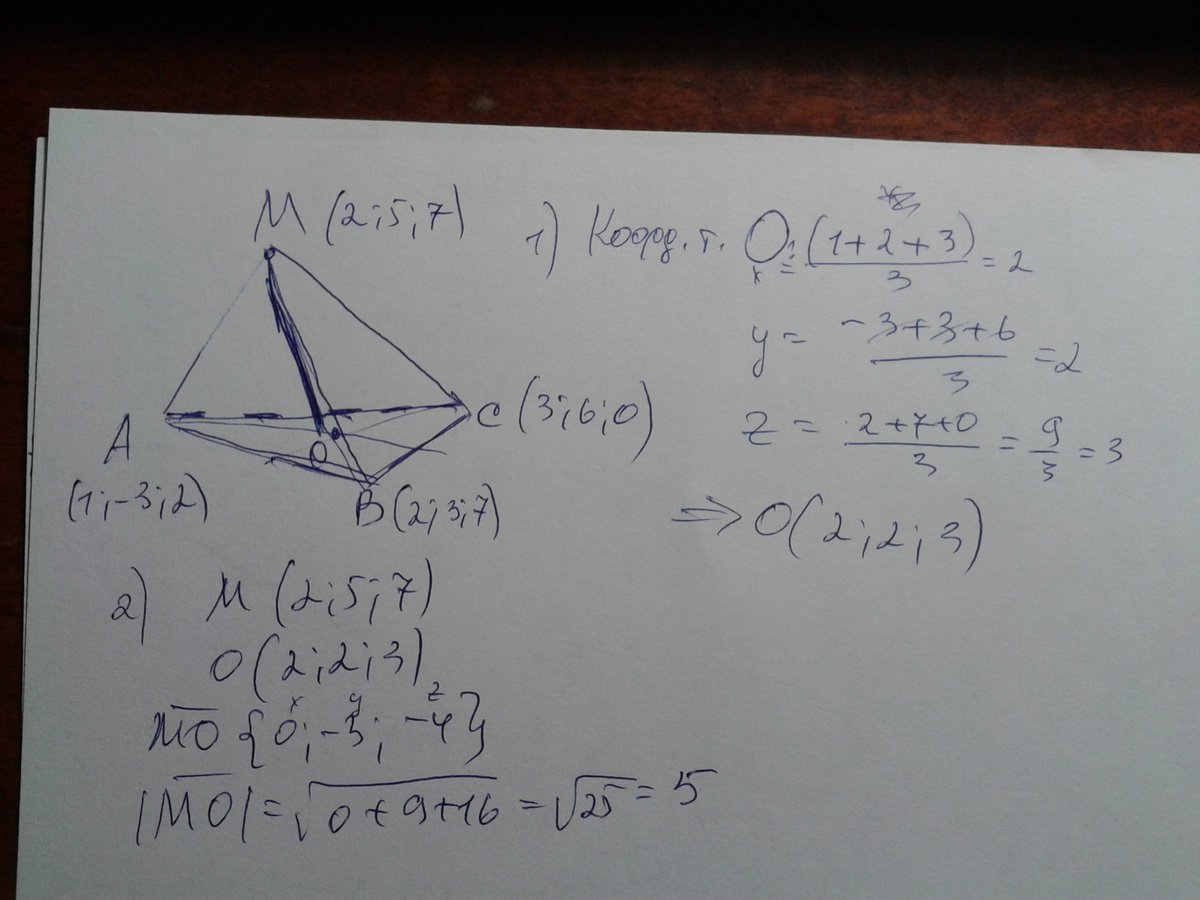Карточка №1 ответы.1.Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление и выбрана единица измерения отрезков, то задается прямоугольная система координат.2.Чтобы найти координаты пересечения медиан одного треугольника, воспользуемся свойством центроида, согласно которому он делит каждую медиану на отрезки 2:1. 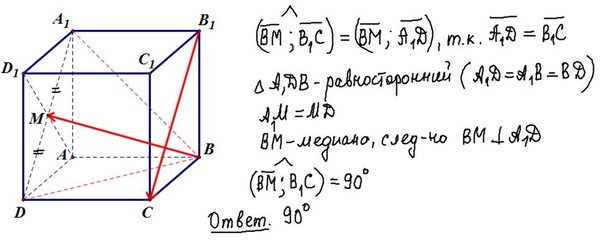Обозначаем вершины как как A(x1;y1), B(x2;y2), C(x3;y3),и вычисляем координаты центра треугольника по формуле: x0 = (x1 + x2 + x3)/3; y0 = (y1 + y2 + y3)/3.3.Перенесем начало вектора B1C в точку М, тогда этот вектор пройдет через точку D. Рассмотрим треугольник BMD. Нужно найти в нем угол BMD, это и будет угол между векторами. 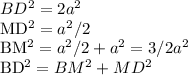По теореме пифагора выразим стороны треугольника через сторону куба.Опять-таки по теореме пифагора, искомый угол равен 90 градусов.Карточка №21. Координаты вектора - это разность координат его конца и координат его начала. 2.3.AB (3-1; -1-1; 0-0) ⇒ AB (2;-2;0)CD (0-4; 1-(-1); 0-2) ⇒ CD(-4; 2; -2)= Карточка №31.Два ненулевых вектора перпендикулярны тогда, когда их скалярное произв. равно 02.3.|AB| = √[ (0-2)^2 + (4-0)^2 + (0-0)^2 ] = √(4 + 16 + 0) = √20|BC| = √[ (2-4)^2 + (0-0)^2 + (0-4)^2 ] = √(4 + 0 + 16) = √20|CD| = √[ (4-2)^2 + (0-4)^2 + (4-4)^2 ] = √(4 + 16 + 0) = √20|DA| = √[ (2-0)^2 + (4-4)^2 + (4-0)^2 ] = √(4 + 0 + 16) = √20Карточка №4

1. 
   
   

2.3.Пусть координаты точки , так как это параллелограмм , то у нее противоположенные стороны равны, иными словами BC=AD . Тогда

---

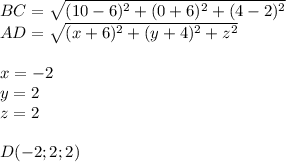
Тогда угол между векторами АС и BD, рассмотрим векторы АС и BD, они имеют координаты по формуле скалярного произведения векторов получаем Ответ к первой задачи координаты точки D(-2;2;2) a=120 гр Карточка №51.движение - отображение пространства на себя, сохраняющее расстояния между точками. а центральная симметрия является примером движения, при котором любая точка пространства М отображается в точку М1 относительно данного центра О - центра симметрии и МО=ОМ1.2. 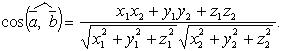3.РЕШУ У ДОСКИ НАВЕРНоКарточка №62.Дык по определению скалярного произведения cos A = (a,b)/(||a||*||b||)3.

---

Смотрите также файлы

• Проектирование локально вычислительной сети на железнодорожном вокзале Барнаула.docx

• Что такое сенсорные эталоны и какова их роль в познавательном развитии.docx

• Реферат по дисциплине Психологопедагогическое взаимодействие участников образовательного процесса Тема сущность функции и уровни общения студент 4 курса заочного отделения.docx

• алтайский государственный колледж.doc

• Амбулаторный автоматизм, аменция, амнезия.docx