Добавлен: 29.10.2023
Просмотров: 12
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ» |
| Кафедра экономики и управления Форма обучения: заочная/очно-заочная |
ВЫПОЛНЕНИЕ
ПРАКТИЧЕСКИХ ЗАДАНИЙ
ПО ДИСЦИПЛИНЕ
_____________________________________________________
Группа ______
Студент
И.О. Фамилия
МОСКВА 20___
Задача 1. Выполнить деление комплексных чисел.
-
.
-
.
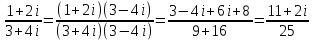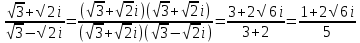Задача 2. Вычислить пределы последовательностей.
2.1.
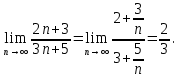
2.2.
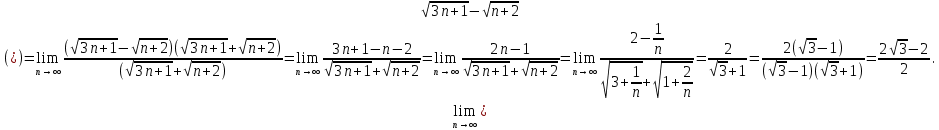
Задача 3. Используя признаки Даламбера и Коши исследовать сходимость рядов.
3.1.
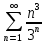, по признаку сходимости Даламбера:
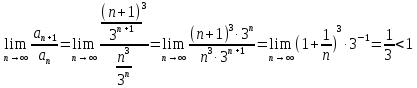, следовательно, исходный ряд сходится.3.2.
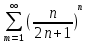, по радикальному признаку Коши:
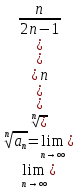, следовательно, исходный ряд сходится.Задача 4. Найти производные сложных функций.
4.1.
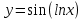
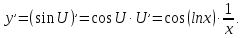
4.2.
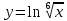
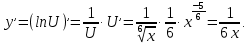
Задача 5. Вычислить неопределенный интеграл.
5.1.
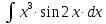
Процесс интегрирования можно упростить
, если сделать замену переменных:
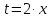
Тогда исходный интеграл можно записать так:
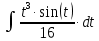
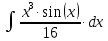
Формула интегрирования по частям:
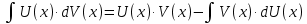
Исходный интеграл представим как:
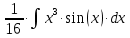
Найдем:
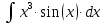
а затем результат домножим на 1/16
Положим:
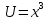
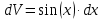
Тогда:
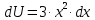
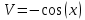
Поэтому:
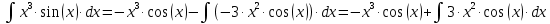
Находим интеграл:
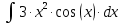
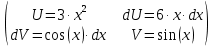
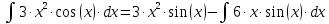
Находим интеграл:
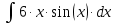
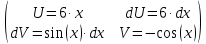
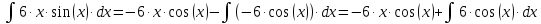
Находим интеграл:
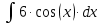
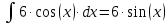
В итоге получаем:
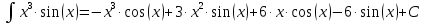
С учетом коэффициента 1/16, получаем
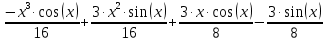
Чтобы записать окончательный ответ, осталось вместо t подставить 2∙x.
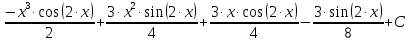.5.2.
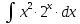
Формула интегрирования по частям:
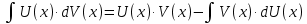
Положим:
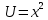
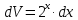
Тогда:
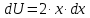
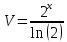
Поэтому:
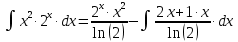
Находим интеграл:
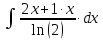
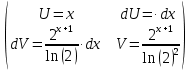
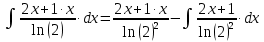
Находим интеграл:
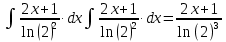
В итоге получаем:
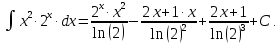
Задание 6. Найти частные производные первого и второго порядка.
6.1.
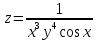
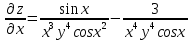
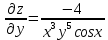
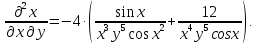
6.2.
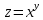
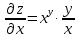
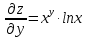
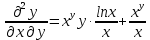.Задание 7. Найти сумму матриц.
7.1.
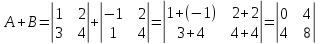.7.2.
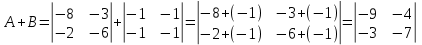.Задание 8. Найти произведение матриц.
8.1.
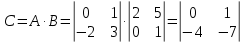
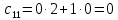
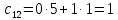
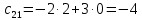
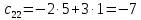
8.2.
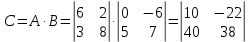
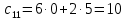
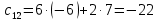
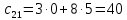
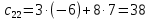
Задача 9. Найдите определители матриц.
9.1.
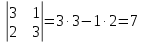.9.2.
.
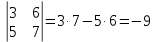
Задача 10. Решить систему уравнений.
10.1.
; 
; 
; 
; 
; 
; 
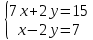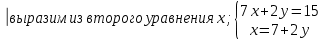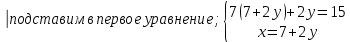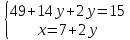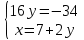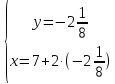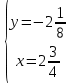.10.2.
; 
; 
;
; 
; 
; 
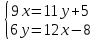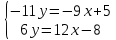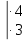
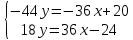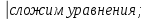
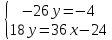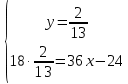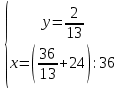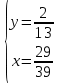.Задача 11. Для заданных векторов найти смешанное произведение
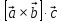.11.1.
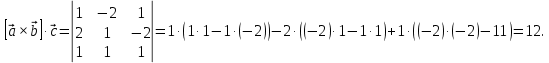
11.2.
.
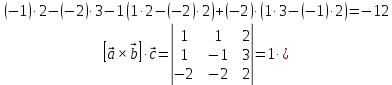