Файл: Содержание Задание Исходные данные Расчет режимов резания и их характеристик Определение диапазона регулирования подач и частот вращения Определение модели станка исходя из расчетных характеристик Задание.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 87
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Принимаем k=12 и корректируем φмех:
φмех =1.1212=3,9
Так как φмех < RдР , то регулирование частоты вращения шпинделя будет происходить при постоянной мощности.
Число ступеней коробки скоростей ограничивается условием:
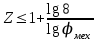 (6.5)
(6.5)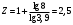
Принимаем Z=2.
Определяем диапазон механического регулирования Rмех и диапазон регулирования привода при постоянной мощности Rp
Rмех= φмех
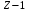 (6.6)
(6.6)Rмех= 3,92-1=3,9
Диапазон регулирования привода при постоянной мощности Rp равен Rp=RдрRмех. Если Rдр=Rмех, то Rp= φмех
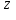
Rp=4·3,9=15,6
Требуемый диапазон полного электрического регулирования Rд и требуемая минимальная частота вращения электродвигателя nдmin:
Rд=
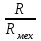 (6.7)
(6.7)nдmin
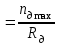 (6.8)
(6.8)Rд=
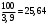
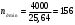 мин
мин 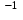
Определяем диапазон регулирования при постоянном моменте:
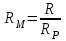 (6.9)
(6.9)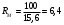
Строим кинематическую схему привода (рис 3.1)
Определяем минимальные частоты вращения шпинделя для каждого диапазона регулирования:
n1min=nmin
n2min=nmin· φмех
···
nzmin=nmin·
n1min=nmin=25 мин
n2min==25·3,9=97.5мин-1
Округляя до стандартной частоты (для φ=1,12), получаем n2min=100 мин-1.
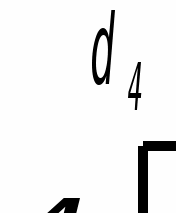
Рисунок 6.1-Кинематическая схема
Определяем минимальную частоту вращения при постоянной мощности и максимальные частоты вращения шпинделя для каждого диапазона:
nzmax=nmax
nz-1max=nzmax/ φмех
nz-2max=nzmax/ φ
мех
···
n1max=nmax/
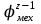
npmin=n1max/RДР
n1max=2500 мин
 мин
мин ;
;npmin=2500/3,9=641 мин

Принимаем стандартную частоту 630 мин
 .
.Определяем число интервалов lg φ, изображающих максимальные частоты вращения шпинделя ymaxи электродвигателя yдmax:
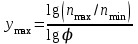 (6.10)
(6.10)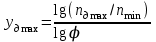 (6.11)
(6.11)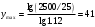
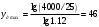
Строим график частот вращения рис 6.2:
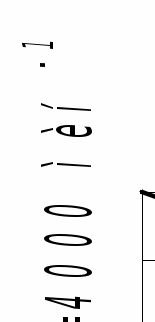
Для φ=1,12 число интервалов, пересекаемые лучом, должно быть не более: для повышающих - 6, для понижающих - 12.
По графику частот вращения определяют передаточные отношения из выражения
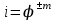 (6.12)
(6.12)где φ - знаменатель геометрического ряда частот вращения,
m - количество интервалов lg φ, пересекаемые лучом, изображающих передачу.
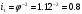
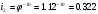
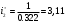
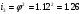
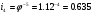
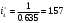
Определяем числа зубьев зубчатых колес (для каждой передачи суммарное число зубьев ∑ zдолжно быть одинаково):
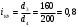 d1=160 мм d2=200 мм
d1=160 мм d2=200 мм 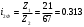 Z
Z =21 Z
=21 Z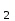 =67 ∑ z=88;
=67 ∑ z=88;
Z
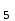 =49 Z
=49 Z =39 ∑ z=88;
=39 ∑ z=88;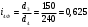 d3=160 мм d4=256 мм
d3=160 мм d4=256 мм Рассчитаем крутящие моменты на валах привода.
Крутящий момент на валу электродвигателя рассчитывается по формуле:
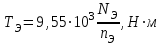 (6.12)
(6.12)Тогда
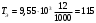 Н·м
Н·мКрутящий момент на каждом последующем валу рассчитывается по формуле:
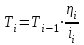 (6.13)
(6.13)где Тi-1 – крутящий момент на предыдущем валу;
ηi – КПД передачи;
ii– передаточное отношение между валами.
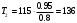 Н·м;
Н·м;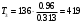 Н·м;
Н·м;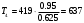 Н·м.
Н·м.7 СИЛОВОЙ, ПРОЧНОСТНОЙ РАСЧЁТ ОСНОВНЫХ ЭЛЕМЕНТОВ ПРИВОДА
7.1 Расчёт поликлиновой ременной передачи
Коэффициент режима работы с учетом двухсменной работы станка СР=0,9
При значении момента T1=637 Н·м выбираем сечение ремня М.
Диаметр меньшего шкива принимаем: dp1=160 мм.
Скорость ведущего шкива:
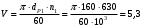 м/с (7.1)
м/с (7.1)Число клиньев ремня определяем по номограммам [5], исходя из v=5,3 м/с, P=12 кВт и u=1.6 принимаем примерное число z=10.
Межосевое расстояние при u=1,6 рассчитываем приближённо по формуле:
a=2·D1=2·160=320 мм, принимаем a=320 мм
Расчётная длина ремня
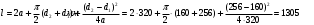 (7.2)
(7.2)Принимаемl=1250 мм.
Уточним межосевое расстояние:
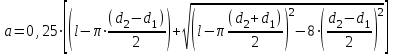 (7.3)
(7.3)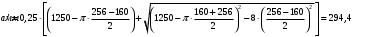
Угол обхвата ремнем ведущего шкива:
=180°-60(d2-d1)/a –в допускаемых пределах.
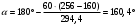
Сила давления на вал:
Fоп=2Fоz sin
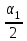 = 50010·sin 160,4/2=4927 H (4.4)
= 50010·sin 160,4/2=4927 H (4.4)Размеры обода шкива поликлинового ремня М показан на рисунке 4.1.

Рисунок 7.1 – Обод шкива для поликлинового ремня
7.2 Расчёт зубчатых передач.
Рассчитаем цилиндрическое зубчатое зацепление с передаточным отношением u=
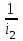 =3,13. Данная передача является прямозубой и состоит из шестерни 1 с числом зубьев z1=21 и колеса 2 с числом зубьев z2=67.
=3,13. Данная передача является прямозубой и состоит из шестерни 1 с числом зубьев z1=21 и колеса 2 с числом зубьев z2=67.Расчет зубчатых передач производим по методике изложенной в [2, 3].
Материал колёс – сталь 40ХН.
Принимаем вариант термообработки: термообработка шестерни и колеса одинаковые – улучшение и закалка ТВЧ твёрдость поверхности 48…53 HRC.
Предел контактной выносливости поверхностей зубьев []Нlim,соответствующий базовому числу циклов напряжений:
а) для шестерни и колеса:
[]Нlim1=17· HRCпов+200 =17·50,5+200=1058,5 МПа (7.5)
Так как средняя твёрдость поверхности зубьев выражена в единицах HRC, переведём в единицы НВ: 50.5 HRC ≈ 480 HB.
Базовое число циклов напряжений NHlim:
NHlim1= NHlim2=30∙H HB12.4=30∙4802.4=81∙106
Эквивалентное число циклов напряжений NHE за расчетный срок службы передачи:
NHE=60∙c1∙n∙Lh∙μH (7.6)
где: c1- число зацеплений зуба шестерни с зубом колеса, c1=1;
n- частота вращения колеса или шестерни, мин-1;
μH - коэффициент, характеризующий интенсивность режима нагружения передачи: μH=0.25 (средний равновероятностный);
Lh- расчетный срок службы передачи, ч
Lh = 365·Lr·tc·Lс,ч;(7.7)
где Lr – срок службы привода, Lr = 10 лет;
tc – продолжительность смены, tc = 8 ч;
Lс – число смен, Lс = 2.
Lh = 365·10·8·2 = 58400ч.
Получаем:
NHE1=60∙1∙800∙58400∙0,25=700∙106
NНЕ2=60∙1∙250∙58400∙0,25=219∙106
Определяем коэффициент долговечности ZN для шестерни и колеса при расчете на контактную усталость:
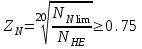 (7.8)
(7.8)а) для шестерни:
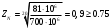
б) для колеса:
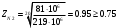
Расчетный коэффициент запаса прочности Sн при расчете на контактную усталость: для шестерни – SH1=1.2, для колеса – SH2=1.2.
Величина допускаемого контактного напряжения при расчете передачи
на контактную усталость:
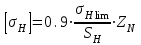 (7.9)
(7.9)Получаем:
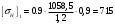 МПа;
МПа;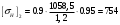 МПа;
МПа;Для дальнейшего расчета принимаем наименьшее допускаемое напряжение: [σH]1=[σH]=715 МПа.
Определяем допускаемое напряжение изгиба при расчете зубьев на усталость при изгибе:
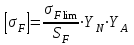 , МПа (4.10)
, МПа (4.10)где σFlim – предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений, МПа;
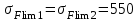 МПа
МПаSF – коэффициент запаса прочности;
YA – коэффициент, учитывающий реверсивность передачи (YA=0,7)
YN – коэффициент долговечности при расчете на изгиб
Рассчитаем эквивалентное число циклов напряжений при расчете на изгиб:
NFE=60∙c∙n∙Lh∙μF
а) для шестерни: NFE1=60∙1∙800∙58400∙0.143=401∙106
б) для колеса: NFE2=60∙1∙250∙58400∙0.143=125∙106
т. к. NFE1>NFlim=4∙106 и NFE2>NFlim=4∙106 то YN=1
Окончательно допускаемое напряжение изгиба:
[σF]1=[σF]2=
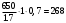 МПа
МПаВ общем виде для зубчатой передачи, состоящей из шестерни и колеса, межосевое расстояние при внешнем зацеплении согласно ГОСТ 21354-87 предварительно определяют из условия контактной выносливости по формуле:
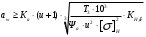 ,мм (7.11)
,мм (7.11)где Ка – вспомогательный коэффициент, Ка = 49,5;
u – передаточное отношение, u = 3,13;
Т3 – вращающий момент на колесе; Н∙м
Ψa – коэффициент ширины венца колеса, Ψa = 0,25;
[σ]H– допускаемое контактное напряжение колеса, МПа;
КНβ – коэффициент неравномерности нагрузки по длине зуба, КНβ = 1.
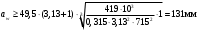
Определяем модуль зубчатых колес исходя из допустимых контактных напряжений:
m =
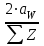 , мм (7.12)
, мм (7.12)Получаем: