Файл: Содержание Задание Исходные данные Расчет режимов резания и их характеристик Определение диапазона регулирования подач и частот вращения Определение модели станка исходя из расчетных характеристик Задание.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 29.10.2023

Просмотров: 88

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите на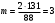м.


мм

Из стандартного ряда выбираем m = 3 мм;

Далее определим модуль зубчатых колес при расчете на изгиб:

m ≥ 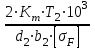, мм (7.13)

где K 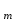- вспомогательный коэффициент. Для прямозубых передач K 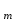= 6,8;

d = 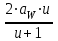- делительный диаметр колеса, мм;

d = 2·131·3,13/(3,13 + 1) = 199 мм;

b = (6…10)·m - ширина венца колеса, мм;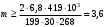

мм

Принимаем m=4 мм.

Уточняем межосевое расстояние:



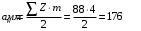
Основные геометрические параметры передачи

;

;

;

;

;

;

.

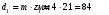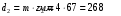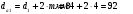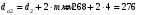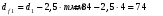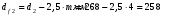Проверочный расчёт


Проверка на контактные напряжения H:

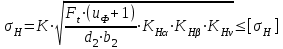(7.14)

где Ft-окружная сила в зацеплении, Н;

Ft=2  T2  103/d2=2  419 103/268=3127 H

K - вспомогательный коэффициент, для прямозубых K=436.

KHα=1 - коэффициент, учитывающий распределение нагрузки между зубьями;

KHv - коэффициент динамической нагрузки. Определяется в зависимости от окружной скорости v:

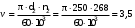м/с (7.15)

Принимаем 8 степень точности.

Принимаем KHv =1,22.



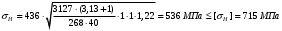
Проверка на напряжения изгиба зубьев шестерни F1 и колеса F2.

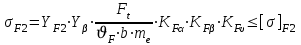(7.16)

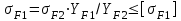(7.17)

где = 1 - коэффициент, учитывающий распределение нагрузки между зубьями;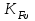

=1,45 - коэффициент динамической нагрузки;

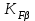=1- коэффициент концентрации нагрузки;

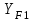=4,04; 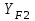=3,65 - коэффициенты формы зуба шестерни и колеса.

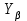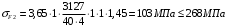
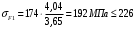=1 - коэффициент, учитывающий наклон зуба.



МПа.

Проверочный расчёт для проектируемой зубчатой передачи выполняется.

Геометрические параметры зубьев зубчатой передачи в этой групповой передаче сведём в таблицу.
Таблица 7.1 – Геометрические параметры первой зубчатой передачи.

Передаточное отношение
Делительный

диаметр, мм
Диаметр вершин, мм

Диаметр

впадин, мм
Ширина

венца, мм

d1
d2
da1
da2
df1
df2
b1
b2

0,319
84
268
92
276
74
258
40
40

1,26
196
156
204
164
186
146
40
40


Произведём расчёт вала III.

В качестве материала изготовления всех валов выбираем сталь 40Х. Определим геометрические параметры ступеней валов.

В первую очередь определяем диаметр первой ступени под зубчатым колесом d1:

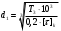(7.18)

где Т – крутящий момент на валу, Н·м.

[τ]k – допускаемое напряжение на кручение, [τ]k = 20…30 МПа.
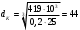мм

Принимаем dк =45 мм.

Вторая ступень под подшипник:

d2 = d1 + 3.2 · f (7.19)

где f – координата фаски в отверстии ступицы шкива, r = 1.6 мм.
d2 = 45 + 3.2 · 1.6= 50.12 мм

принимаем dб = 50 мм, что соответствует диаметрам внутренних колец подшипников. Исходя из размера по табл. 2П15 приложения 2П [2] выбираем шариковый радиальный подшипник средней серии 210 ГОСТ 8338-75 (D=90 мм, B=20 мм, r=2 мм; Сr=35,1 кН)

Третья ступень вала диаметром d3 служит в качестве буртика для упора подшипника. По табл. 2П.18 приложения 2П [1] для выбранного подшипника легкой серии с d=40 мм наружный диаметр буртика со стороны подшипника dб.п.=57 мм.

Принимаем шлицевое соединение с центрированием по наружному диаметру:



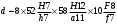
Диаметры ступеней остальных валов сведем в таблицу 7.2:
Таблица 7.2 – Диаметры ступеней валов
Диаметр под зубчатым колесом
Диаметр под подшипник
Диаметр упорной ступени

Вал II
34
40
47

Вал III
45
50
8х52х58х10


Шлицевое соединение под зубчатыми колесами, длина ступиц которых составляет lст=60 мм. Материал ступицы колеса – сталь 40Х. Принимаем посадку колеса на вал – подвижное со средними условиями работы. Допускаемое напряжение на смятие боковых сторон зубьев шлицевого соединения[sсм]=50 МПа.

Расчетное напряжение смятия при вращающем моменте на валу Т=419 Н ·м:


см= 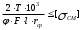, (4.20)

где Т- передаваемый вращающий момент, Н ·м;

φ- коэффициент, учитывающий неравномерность распределения нагрузок по рабочим поверхностям зубьев;

F – площадь всех боковых поверхностей зубьев с одной стороны на 1 мм длины, мм2/мм;

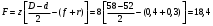мм2

f и r – соответственно размер фаски и скругления, мм;

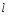- рабочая длина зуба, мм;

rср– средний диаметр, мм;

см= 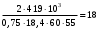МПа

что меньше [sсм]=50 МПа.

7.3 Расчёт вала на сопротивление усталости.

Произведем расчёт III вала, так как он наиболее нагруженого.

Для определения направления действия сил в зубчатом зацеплении изобразим свёртку коробки скоростей и спроецируем все силы на оси координат рис. 4.2:

Силы, действующие на вал: Ft2=3127 H, Fr2= Ft2·tgα=3127·tg20º=1138 H, Fв=4927 Н.

Рисунок 4.2 – Схема нагружения вала
Плоскость YOX

Радиальные реакции опор от сил в вертикальной плоскости YOZ:

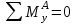; -Ft2·l2+RBy·( l2+l3)=0

RBy=

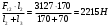
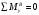; -Ft2·l3 +RAy·( l2+l3)=0

RAy=

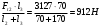
Проверка: 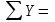RAy+ RBy – Ft2 =912+2215–3127=0 – реакции найдены правильно.

Для построения эпюр определяем значения изгибающих моментов в характерных сечениях вала.

Сечение A: M=0

Сечение С: M= RAy·l2=-912·0.17= 155 Н·м.

Сечение B: M=0


Рисунок 7.2 – Разложение сил на плоскости.
Плоскость XOZ

Радиальные реакции опор от сил в вертикальной плоскости YOZ:

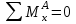; - RBx·(l2+l3)-Fr2·l2+Fв· l1=0

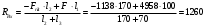Н


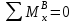; RAx·(l2+l3)+Fr2·l3 +Fв·( l1+l2+l3)=0

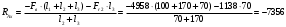Н

Проверка: 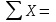RAx + RBx+ Fr2+ Fв=0

–7356+1260+4958+1138=0 – реакции найдены правильно.

Для построения эпюр определяем значения изгибающих моментов в характерных сечениях вала.

Сечение О: M=0

Се чение А: M= Fв·l1=4958·0.1= 496 Н·м.

Сечение C: M= RAx·l2 + Fв·(l1+ l2)= –7356·0.17+4958·(0.1+0,17)=88 Н·м.

Сечение В: M=0

Рисунок 7.3- Разложение сил на плоскости
Передача вращающего момента происходит вдоль оси вала от сечения D к сечению У: Мк=Т3=419 Н·м.

Рисунок 2.4 – Эпюра крутящих моментов.
Определяем суммарные реакции в подшипниках:


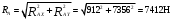
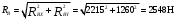
Определяем суммарные изгибающие моменты в наиболее нагруженных точках.



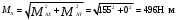
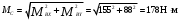
Проверочный расчёт вала.

Проверочный расчёт вала на прочность выполняют на совместное действие изгиба и кручения.

Цель расчёта – определить коэффициенты запаса прочности в опасных сечениях вала и сравнить их с допускаемыми [S], принимаемым обычно 1,5.
S = 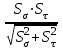≥ [S] (7.21)
где Sσ и Sτ – коэффициенты запаса по нормальным и касательным напряжениям.

Наиболее опасное сечение вала является сечение А, где концентратором напряжения является – посадка внутреннего кольца подшипника на вал и канавка для выхода шлифовального круга.

Концентратор напряжений – посадка внутреннего кольца подшипника на валу переходная. По табл. 14.5 [1] при σВ=800 МПа для валов посадки II Кσ/Кd=2,97 и Кτ/Кd=2,28.

Концентратор напряжений – ступенчатый переход с канавкой для выхода шлифовального круга. Для ступенчатого перехода от ступени вала диаметром d=50 мм к ступени диаметром D=58 мм при радиусе канавки для выхода шлифовального круга r=1 мм определим отношения: D/d=58/50=1,16; r/d=1/50=0.02. По табл. 14.3 [1] при σ

Смотрите также файлы