ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 275
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
•E. В зависимости от диаграммы рассеяния яркость по разным направлениям может быть различна, и вычисление ее представляет очень сложную задачу. Задача эта упрощается, если поверхность рассеивает свет равномерно по всем направлениям. В таком случае и яркость по всем направлениям будет одинаковой и равной
23) Световые измерения и измерительные приборы. Измерение световых величин может производиться непосредственно с помощью глаза (визуальные методы) или с помощью фотоэлемента, или термостолбика (объективные методы). Приборы, служащие для измерения световых величин, называются хфотометрами.
Визуальные методы основаны на свойстве глаза очень хорошо устанавливать равенство яркостей двух смежных поверхностей. В то же время с помощью глаза очень трудно оценить, во сколько раз яркость одной поверхности больше яркости второй. Поэтому во всех визуальных фотометрах роль глаза сводится к установлению равенства яркостей двух смежных площадок, освещаемых сравниваемыми источниками.
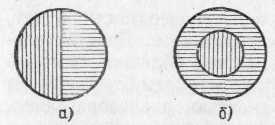
Так как сравниваемые поверхности делаются диффузно отражающими, то равенство их яркостей соответствует, согласно сказанному в предыдущем параграфе, равенству освещенностей. Освещенность площадки, на которую падает свет от более сильного источника, ослабляется тем или иным способом в известное число раз. Установив равенство освещенностей обеих площадок и зная, во сколько раз ослаблен свет одного из источников, мы можем количественно сравнить силы света обоих источников. Таким образом, во всяком фотометре должны быть два смежных световых поля, одно из которых освещено только одним источником, второе — только другим. Вид сравниваемых полей может быть различен. В большинстве случаев они имеют форму двух смежных полукругов (рис. 164, а) или двух концентрических кругов (рис. 164, б).Оба сравниваемых поля должны освещаться каждое своим источником под одним и тем же углом; глаз наблюдателя также должен рассматривать оба поля под одинаковыми углами зрения.
24. Основы геометрической оптики.
В основе геометрической оптики лежат четыре основных закона.
Закон независимости световых лучей
Закон прямолинейного распространения света
Закон отражения света
Закон преломления света
25. Законы отражения и преломления света. Понятие дисперсии.
Законы отражения
Плоская граница раздела, от которой свет только отражается, называется плоским зеркалом. Если есть точечный источник S света, то его изображение S* в плоском зеркале находится симметрично зеркалу и является мнимым.
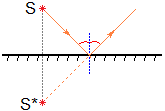
В
се лучи, которые от источника падают на зеркало, отражаются так, что продолжения этих лучей пересекаются в точке, где находится изображение. При этом, конечно же, выполняются все законы отражения света.
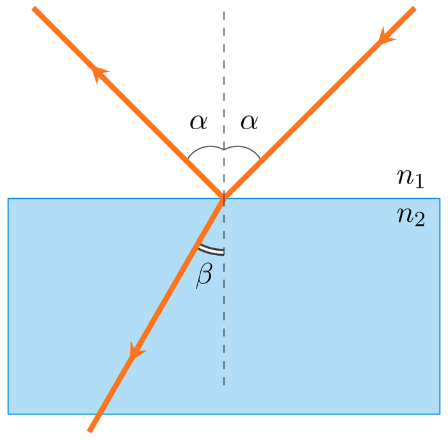
Дисперсия света (разложение света) — это явление, обусловленное зависимостью абсолютного показателя преломления вещества от частоты (или длины волны) света (частотная дисперсия), или, то же самое, зависимость фазовой скорости света в веществе от длины волны (или частоты).
26. Интерференция света. Дифракция света. Поляризация света.
ДИСПЕРСИЯ СВЕТА
Зависимость показателя преломления света от частоты колебаний (или длины волны) называется дисперсией. Разложение белого света в спектр есть следствие дисперсии. Впервые исследовал дисперсию И. Ньютон. Почему белый свет, входящий в призму в виде круглого пучка, выходит из призмы продолговатой разноцветной полосой? Направив эту полосу на вторую призму, Ньютон получил белый свет. Белый свет сложный. Ньютон выделил в нем семь цветов: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый.
27. Линзы. Преломление изображения в линзах.
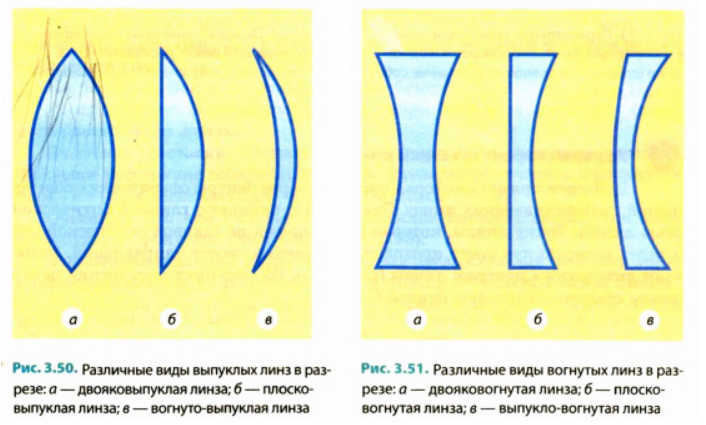
Обычно выпуклые линзы являются собирающими: параллельные лучи, которые падают на собирающую линзу, пройдя сквозь нее, пересекаются в одной точке.
Вогнутые линзы чаще всего бывают рассеивающими: параллельные лучи после прохождения сквозь рассеивающую линзу выходят расходящимся пучком.
28. Формула линзы. Действительное и мнимое изображение.
Изображение, которое получено пересечением реальных световых лучей, называют действительным изображением.
Мнимым изображением называют изображение, которое получено в результате пересечения не реальных световых лучей, а их воображаемых продолжений.
29. Плоские и сферические зеркала.
Плоское зеркало — это плоская поверхность, зеркально отражающая свет.
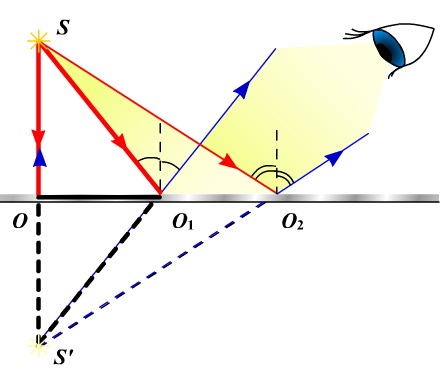
Изображение в плоском зеркале является:
Сферическим зеркалом называют зеркально отражающую поверхность, имеющую форму сферического сегмента.
Центр сферы, из которой вырезан сегмент, называют оптическим центром зеркала. Вершину сферического сегмента называют полюсом. Прямая, проходящая через оптический центр и полюс зеркала, называется главной оптической осью сферического зеркала. Главная оптическая ось выделена из всех других прямых, проходящих через оптический центр, только тем, что она является осью симметрии зеркала.
Сферические зеркала бывают вогнутыми и выпуклыми. Если на вогнутое сферическое зеркало падает пучок лучей, параллельный главной оптической оси, то после отражения от зеркала лучи пересекутся в точке, которая называется главным фокусом
F зеркала. Расстояние от фокуса до полюса зеркала называют фокусным расстоянием и обозначают той же буквой F. У вогнутого сферического зеркала главный фокус действительный. Он расположен посередине между центром и полюсом зеркала.
30. Построение изображения в зеркалах.
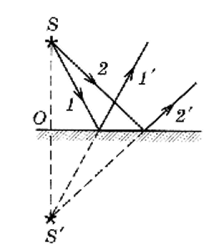
Плоское зеркало — плоская полированная поверхность, при отражении от которой параллельный пучок остается параллельным. Построим изображение точечного источника 5 (рис. 6) в плоском зеркале. Два произвольных луча 1 и 2, исходящие из точки 5, отражаясь от зеркала в соответствии с законом отражения, расходятся. Продолжения этих лучей пересекаются в точке Б', находящейся по другую сторону зеркала относительно 5. 5' и является мнимым изображением точечного источника, оно образуется при пересечении не самих лучей, а их продолжений.
При построении изображения точки в сферическом зеркале следует воспользоваться любыми двумя лучами из следующих трех (рис. 8):
1) луч 1, параллельный главной оптической оси зеркала, который после отражения от зеркала проходит через главный фокус;
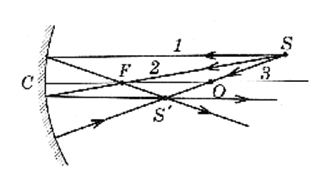
Рис. 8
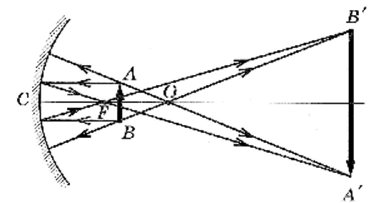
Рис. 9
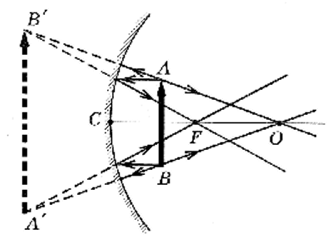
Рис. 10
На рис. 9—11 для примера построены изображения предмета в вогнутом сферическом зеркале. Так, если предмет расположен между фокусом и оптическим центром: изображение перевернутое
, увеличенное, действительное (см. рис. 9); предмет между фокусом и зеркалом: изображение прямое, увеличенное, мнимое (см. рис. 10); предмет расположен дальше оптического центра: изображение перевернутое, уменьшенное, действительное (см. рис. 11).
Из рис. 12 следует, что в выпуклом сферическом зеркале при любом положении предмета изображение будет прямым, уменьшенным и мнимым.
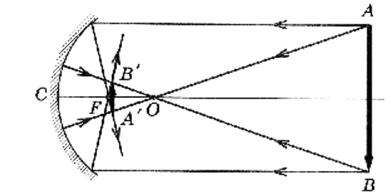
Рис. 1 1
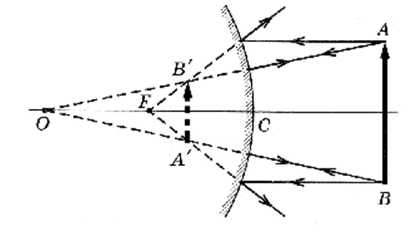
Рис. 12
31. Увеличение при изображении объектов в сферических зеркалах и линзах.
В отличие от случая плоского зеркала, размер изображения, даваемого сферическим зеркалом, будет меняться в зависимости от положения объекта по отношению к фокусу зеркала.
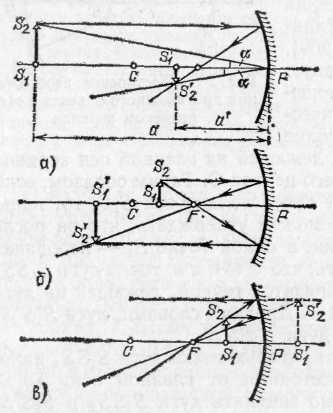
Если объект находится много дальше фокуса вогнутого зеркала, то его изображение получается уменьшенным. Если объект находится между зеркалом и фокусом, то изображение получается мнимым и увеличенным.
Отношение линейных размеров изображения S1'S2'=у' к линейным размерам предмета S1S2=y называется линейным, или поперечным, увеличением:
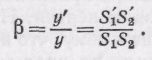
Изображения, получаемые с помощью линзы, могут Выть также увеличенными и уменьшенными. Из подобия треугольников S1OS2 и S1'OS2' находим для увеличения линзы точно такое же выражение, какое мы получили для сферического зеркала:
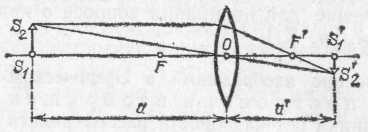
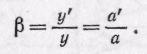
Наряду с линейным увеличением мы будем рассматривать также угловое увеличение линзы (или сферического зеркала). Угловым увеличением у называется отношение тангенсов углов, составляемых лучом, выходящим из линзы, и лучом, падающим на линзу, с оптической осью, т. е. угловое увеличение есть величина, обратная линейному увеличению. Из этого следует, что чем больше линейное увеличение, т. е. размеры изображения, тем меньше угловое увеличение, т. е. тем менее широки пучки световых лучей, образующих изображение. Это обстоятельство имеет важное значение для понимания вопроса о яркости изображения.
23) Световые измерения и измерительные приборы. Измерение световых величин может производиться непосредственно с помощью глаза (визуальные методы) или с помощью фотоэлемента, или термостолбика (объективные методы). Приборы, служащие для измерения световых величин, называются хфотометрами.
Визуальные методы основаны на свойстве глаза очень хорошо устанавливать равенство яркостей двух смежных поверхностей. В то же время с помощью глаза очень трудно оценить, во сколько раз яркость одной поверхности больше яркости второй. Поэтому во всех визуальных фотометрах роль глаза сводится к установлению равенства яркостей двух смежных площадок, освещаемых сравниваемыми источниками.
Так как сравниваемые поверхности делаются диффузно отражающими, то равенство их яркостей соответствует, согласно сказанному в предыдущем параграфе, равенству освещенностей. Освещенность площадки, на которую падает свет от более сильного источника, ослабляется тем или иным способом в известное число раз. Установив равенство освещенностей обеих площадок и зная, во сколько раз ослаблен свет одного из источников, мы можем количественно сравнить силы света обоих источников. Таким образом, во всяком фотометре должны быть два смежных световых поля, одно из которых освещено только одним источником, второе — только другим. Вид сравниваемых полей может быть различен. В большинстве случаев они имеют форму двух смежных полукругов (рис. 164, а) или двух концентрических кругов (рис. 164, б).Оба сравниваемых поля должны освещаться каждое своим источником под одним и тем же углом; глаз наблюдателя также должен рассматривать оба поля под одинаковыми углами зрения.
24. Основы геометрической оптики.
В основе геометрической оптики лежат четыре основных закона.
Закон независимости световых лучей
Закон прямолинейного распространения света
Закон отражения света
Закон преломления света
25. Законы отражения и преломления света. Понятие дисперсии.
Законы отражения
-
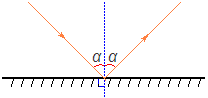
Луч падающий, луч отраженный и перпендикуляр, восстановленный в точке падения, лежат в одной плоскости. -
Угол падения равен углу отражения.
Плоская граница раздела, от которой свет только отражается, называется плоским зеркалом. Если есть точечный источник S света, то его изображение S* в плоском зеркале находится симметрично зеркалу и является мнимым.
В
се лучи, которые от источника падают на зеркало, отражаются так, что продолжения этих лучей пересекаются в точке, где находится изображение. При этом, конечно же, выполняются все законы отражения света. Дисперсия света (разложение света) — это явление, обусловленное зависимостью абсолютного показателя преломления вещества от частоты (или длины волны) света (частотная дисперсия), или, то же самое, зависимость фазовой скорости света в веществе от длины волны (или частоты).
26. Интерференция света. Дифракция света. Поляризация света.
ДИСПЕРСИЯ СВЕТА
Зависимость показателя преломления света от частоты колебаний (или длины волны) называется дисперсией. Разложение белого света в спектр есть следствие дисперсии. Впервые исследовал дисперсию И. Ньютон. Почему белый свет, входящий в призму в виде круглого пучка, выходит из призмы продолговатой разноцветной полосой? Направив эту полосу на вторую призму, Ньютон получил белый свет. Белый свет сложный. Ньютон выделил в нем семь цветов: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый.
27. Линзы. Преломление изображения в линзах.
Обычно выпуклые линзы являются собирающими: параллельные лучи, которые падают на собирающую линзу, пройдя сквозь нее, пересекаются в одной точке.
Вогнутые линзы чаще всего бывают рассеивающими: параллельные лучи после прохождения сквозь рассеивающую линзу выходят расходящимся пучком.
28. Формула линзы. Действительное и мнимое изображение.
Изображение, которое получено пересечением реальных световых лучей, называют действительным изображением.
Мнимым изображением называют изображение, которое получено в результате пересечения не реальных световых лучей, а их воображаемых продолжений.
29. Плоские и сферические зеркала.
Плоское зеркало — это плоская поверхность, зеркально отражающая свет.
Изображение в плоском зеркале является:
-
прямым; -
мнимым; -
равным по величине предмету: h = H.
Сферическим зеркалом называют зеркально отражающую поверхность, имеющую форму сферического сегмента.
Центр сферы, из которой вырезан сегмент, называют оптическим центром зеркала. Вершину сферического сегмента называют полюсом. Прямая, проходящая через оптический центр и полюс зеркала, называется главной оптической осью сферического зеркала. Главная оптическая ось выделена из всех других прямых, проходящих через оптический центр, только тем, что она является осью симметрии зеркала.
Сферические зеркала бывают вогнутыми и выпуклыми. Если на вогнутое сферическое зеркало падает пучок лучей, параллельный главной оптической оси, то после отражения от зеркала лучи пересекутся в точке, которая называется главным фокусом
F зеркала. Расстояние от фокуса до полюса зеркала называют фокусным расстоянием и обозначают той же буквой F. У вогнутого сферического зеркала главный фокус действительный. Он расположен посередине между центром и полюсом зеркала.
30. Построение изображения в зеркалах.
Плоское зеркало — плоская полированная поверхность, при отражении от которой параллельный пучок остается параллельным. Построим изображение точечного источника 5 (рис. 6) в плоском зеркале. Два произвольных луча 1 и 2, исходящие из точки 5, отражаясь от зеркала в соответствии с законом отражения, расходятся. Продолжения этих лучей пересекаются в точке Б', находящейся по другую сторону зеркала относительно 5. 5' и является мнимым изображением точечного источника, оно образуется при пересечении не самих лучей, а их продолжений.
При построении изображения точки в сферическом зеркале следует воспользоваться любыми двумя лучами из следующих трех (рис. 8):
1) луч 1, параллельный главной оптической оси зеркала, который после отражения от зеркала проходит через главный фокус;
Рис. 8
Рис. 9
Рис. 10
-
2) луч 2, проходящий через главный фокус, который после отражения от зеркала идет параллельно главной оптической оси; -
3) луч 3, проходящий через оптический центр зеркала, который после отражения от зеркала идет вдоль падающего луча в противоположном направлении.
На рис. 9—11 для примера построены изображения предмета в вогнутом сферическом зеркале. Так, если предмет расположен между фокусом и оптическим центром: изображение перевернутое
, увеличенное, действительное (см. рис. 9); предмет между фокусом и зеркалом: изображение прямое, увеличенное, мнимое (см. рис. 10); предмет расположен дальше оптического центра: изображение перевернутое, уменьшенное, действительное (см. рис. 11).
Из рис. 12 следует, что в выпуклом сферическом зеркале при любом положении предмета изображение будет прямым, уменьшенным и мнимым.
Рис. 1 1
Рис. 12
31. Увеличение при изображении объектов в сферических зеркалах и линзах.
В отличие от случая плоского зеркала, размер изображения, даваемого сферическим зеркалом, будет меняться в зависимости от положения объекта по отношению к фокусу зеркала.
Если объект находится много дальше фокуса вогнутого зеркала, то его изображение получается уменьшенным. Если объект находится между зеркалом и фокусом, то изображение получается мнимым и увеличенным.
Отношение линейных размеров изображения S1'S2'=у' к линейным размерам предмета S1S2=y называется линейным, или поперечным, увеличением:
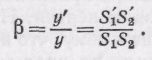
Изображения, получаемые с помощью линзы, могут Выть также увеличенными и уменьшенными. Из подобия треугольников S1OS2 и S1'OS2' находим для увеличения линзы точно такое же выражение, какое мы получили для сферического зеркала:
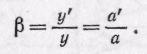
Наряду с линейным увеличением мы будем рассматривать также угловое увеличение линзы (или сферического зеркала). Угловым увеличением у называется отношение тангенсов углов, составляемых лучом, выходящим из линзы, и лучом, падающим на линзу, с оптической осью, т. е. угловое увеличение есть величина, обратная линейному увеличению. Из этого следует, что чем больше линейное увеличение, т. е. размеры изображения, тем меньше угловое увеличение, т. е. тем менее широки пучки световых лучей, образующих изображение. Это обстоятельство имеет важное значение для понимания вопроса о яркости изображения.