ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 40
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
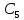 , если исходная концентрация была равна
, если исходная концентрация была равна 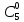 = 0,1 моль/дм3 (температура раствора 200С, масса адсорбента 4 г).
= 0,1 моль/дм3 (температура раствора 200С, масса адсорбента 4 г). Таблица 7
Исходные
 и равновесные
и равновесные  концентрации раствора уксусной кислоты при адсорбции на угле (t = 200С, масса угля m= 4г)
концентрации раствора уксусной кислоты при адсорбции на угле (t = 200С, масса угля m= 4г)| Исходная концентрация раствора  , моль/дм3 , моль/дм3 | Равновесная концентрация раствора  , моль/дм3 , моль/дм3 | |||||||||
 |  |  |  | 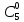 | 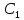 | 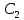 | 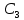 | 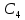 | 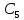 | |
| 0,18 | 0,28 | 0,38 | 0,48 | 0,1 | 0,148 | 0,24 | 0,334 | 0,429 | ? | |
Уравнение Фрейндлиха для адсорбции из раствора на твердом адсорбенте имеет вид
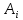 =
= 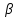
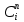 , (12)
, (12)где
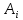 – адсорбция – масса адсорбированного вещества на единицу массы адсорбента, моль/г;
– адсорбция – масса адсорбированного вещества на единицу массы адсорбента, моль/г;
 – равновесная концентрация раствора, моль/дм3;
– равновесная концентрация раствора, моль/дм3; и n – постоянные при данной температуре.
и n – постоянные при данной температуре.Прологарифмируем уравнение (12)
lg
 = n lg
= n lg  + lg
+ lg  (13)
(13)Если в рассматриваемом случае адсорбция записывается уравнением Фрейндлиха, то в координатах lg
 – lg
– lg  график функции должен представлять прямую.
график функции должен представлять прямую.Изотерма адсорбции Лэнгмюра имеет вид
 =
= 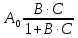 (14)
(14)где
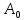 – предельная адсорбция, соответствующая полному заполнению поверхности адсорбента молекулами адсорбента, моль/г;
– предельная адсорбция, соответствующая полному заполнению поверхности адсорбента молекулами адсорбента, моль/г; В – постоянная, зависящая для данной системы от температуры.
После несложных преобразований уравнение (14) можно представить в линейной, удобной для графического представления форме
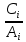 =
= 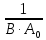 +
+ 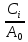 (15)
(15)Если рассматриваемый случай описывается изотермой Лэнгмюра, то в координатах
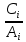 = f(
= f( ) график должен соответствовать прямой линии.
) график должен соответствовать прямой линии.Для установления, каким из адсорбционных уравнений Фрейндлиха или Лэнгмюра описывается адсорбция в рассматриваемом случае, рассчитаем величину адсорбции при различных концентрациях раствора
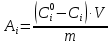 (16)
(16)где
 – число моделей вещества, адсорбированного из V литров раствора на m граммах адсорбента при исходной и равновесной концентрациях
– число моделей вещества, адсорбированного из V литров раствора на m граммах адсорбента при исходной и равновесной концентрациях 
и
 соответственно.
соответственно.После подстановки данных задачи (m = 4 г, V = 0,2 дм3) выражение имеет вид
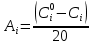 (17)
(17)Найденные по уравнению (17) значения
 вместе с величинами lg
вместе с величинами lg  , lg
, lg  ; и
; и  сведем в табл. 8.
сведем в табл. 8. Таблица 8
Данные для построения изотерм адсорбции
| Исходная концентрация раствора  , моль/дм3 , моль/дм3 | Равновесная концентрация раствора  , моль/дм3 , моль/дм3 | Величина адсорбции  · ·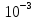 , моль/г , моль/г | – lg  | – lg  |  , г/дм3 , г/дм3 |
| 0,18 | 0,148 | 1,6 | 0,829 | 2,795 | 92,5 |
| 0,28 | 0,24 | 2 | 0,619 | 2,698 | 120 |
| 0,38 | 0,334 | 2,3 | 0,476 | 2,638 | 145,217 |
| 0,48 | 0,429 | 2,55 | 0,367 | 2,593 | 168,235 |
График в координатах lg
 – lg
– lg  , представленный на рис.5. представляет собой прямую, т.е. рассматриваемый случай описывается изотермой адсорбции Фрейндлиха.
, представленный на рис.5. представляет собой прямую, т.е. рассматриваемый случай описывается изотермой адсорбции Фрейндлиха.
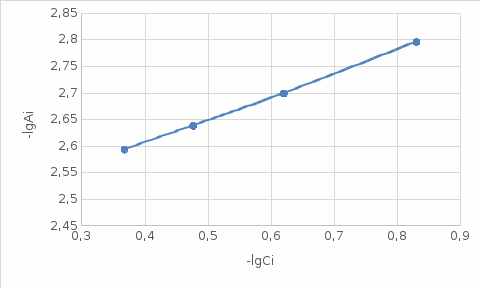
Рисунок 5. Зависимость величины адсорбции lg
 от равновесной концентрации lg
от равновесной концентрации lg 
-
Исследование процесса адсорбции, описываемого уравнением Фрейндлиха
На графике в координатах lg
 – lg
– lg  (рис.5.) прямая, и это свидетельствует о том, что процесс адсорбции описывается уравнением Фрейндлиха (12 - 13).
(рис.5.) прямая, и это свидетельствует о том, что процесс адсорбции описывается уравнением Фрейндлиха (12 - 13). В этом случае постоянные n и β в уравнении Фрейндлиха
lg
 = n lg
= n lg  + lg
+ lg 
n - можно вычислить из графика (см. рис. 5) как тангенс угла наклона прямой
n = tgα =
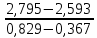 = 0,437 (20)
= 0,437 (20)и затем определить значение lg β из уравнения (13), взяв из графика (см. рис.5) любое значение lg A и соответствующее ему значение lg C.
lg
 = lg A –n lg C = – 2,795 – 0,437 · (–0,829) = -2,432 (21)
= lg A –n lg C = – 2,795 – 0,437 · (–0,829) = -2,432 (21)И затем определить значение β из выражения
 =
= 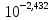 = 0,0037 (22)
= 0,0037 (22)Приравняв правые части уравнений (12) и (17) с численными значениями констант n и
 , решая его относительно
, решая его относительно  , получается степенное уравнение вида
, получается степенное уравнение вида20 ·
 ·
· 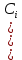 +
+  –
–  = 0, (23)
= 0, (23)где n – дробное число,
 =
=  – исходная концентрация пятого раствора, для которого нужно определить равновесную концентрацию.
– исходная концентрация пятого раствора, для которого нужно определить равновесную концентрацию.
20 · 0,0037 ·
 +
+  –
–  = 0, (24)
= 0, (24)Уравнение (24) при дробном значении n можно решить методом подбора, подставляя в него значения
 из интервала от 0 до
из интервала от 0 до  исходя из очевидного, что равновесная концентрация не может быть нулевой и не может превышать исходную –
исходя из очевидного, что равновесная концентрация не может быть нулевой и не может превышать исходную –  .
.20 · 0,0037 ·
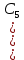 +
+  –
–  = 0
= 020 · 0,0037 ·
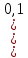 + 0,1 –
+ 0,1 – 
 0.
0.Поэтому
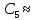 0,127.
0,127.-
Исследование процесса адсорбции, описываемого уравнением Лэнгмюра
Рассматриваемый случай не описывается изотермой Лэнгмюра, так как в координатах
 = f(
= f( ) график не представляет прямую. По данным табл. 8 построена зависимость в указанных координатах, представлена на рис.6.
) график не представляет прямую. По данным табл. 8 построена зависимость в указанных координатах, представлена на рис.6.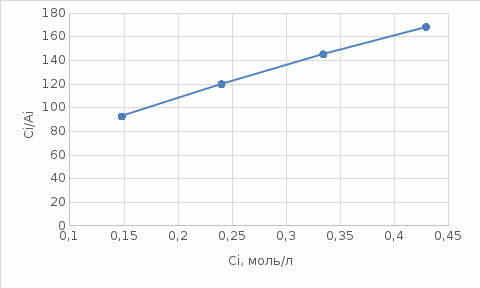
Рисунок 6. Изотерма Лэнгмюра в координатах
 = f(
= f( )
)