ЗАДАНИЕ: Операция тонкого шлифования шейки вала диаметром 12-0,011

Цена деления прибора C, мм				0,010
Результаты измерений, мм
1: 11,989	10: 11,995	19: 11,989
2: 11,998	11: 11,99	20: 11,989
3: 11,992	12: 11,992	21: 11,992
4: 11,997	13: 11,995	22: 12,00
5: 11,998	14: 11,99	23: 12,00
6: 12,00	15: 11,992	24: 11,995
7: 12,00	16: 11,997	25: 11,995
8: 11,989	17: 11,995
9: 11,99	18: 1,998

1.Построение гистограммы
Определяем величину размаха R (поле рассеяния):
R = Xmax - Xmin
Xmax = 12,00 – наибольшее из измеренных значений

Xmin = 11,989 – наименьшее из измеренных значений
R = Xmax - Xmin = 0,011 (мм).
Определяем число интервалов разбиения n, в соответствии с рекомендациями:
n  √ N  5

( количество интервалов принимается ближайшим большим нечетным ).
Принимаем n = 5
Определяем ширину интервала h: h  R/n = 0,0022 мм.

Определяем границы интервалов Xmin

---

i – Xmaxi
1 интервал: Xmin1 – Xmax1
Xmin1 = Xmin= 11,989 мм
Xmax1 = Xmin1 + h = 11,9912 мм
2 интервал: Xmin2 – Xmax2
Xmin2 = Xmax1 = 11,9912 (мм)
Xmax2 = Xmin2 + h = 11,9934 (мм)
3 интервал: Xmin3 – Xmax3
Xmin3 = Xmax2 = 11,9934 (мм)
Xmax3 = Xmin3 + h = 11,9956 (мм)
4 интервал: Xmin4 – Xmax4
Xmin4 = Xmax3 = 11,9956 (мм)
Xmax4 = Xmin4 + h = 11,9978 (мм)
5 интервал: Xmin5 – Xmax5
Xmin5 = Xmax4 = 11,9978 (мм)
Xmax5 = Xmin5 + h = 12 (мм)

Определение количества размеров попадающих в каждый интервал mi
Используя заданную выборку подсчитываем количество размеров попадающих в каждый интервал (если размер совпадает с границей интервала то его относят в интервал, находящийся слева по числовой оси )



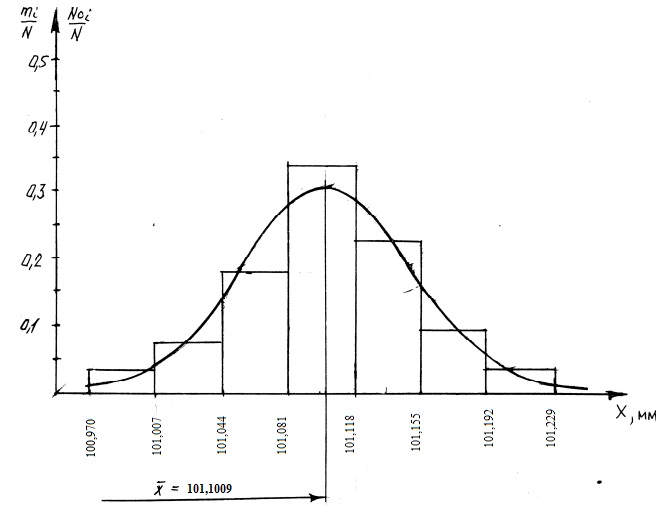
Результаты выполненных выше расчетов занесем в таблицу:
2.Проверка выборки на соответствие нормальному закону распределения
При числе измерений свыше 50 проверка распределения на соответствие нормальному закону может выполняться по критерию Пирсона. При использовании этого критерия определяется параметр хи-квадрат по следующей формуле:
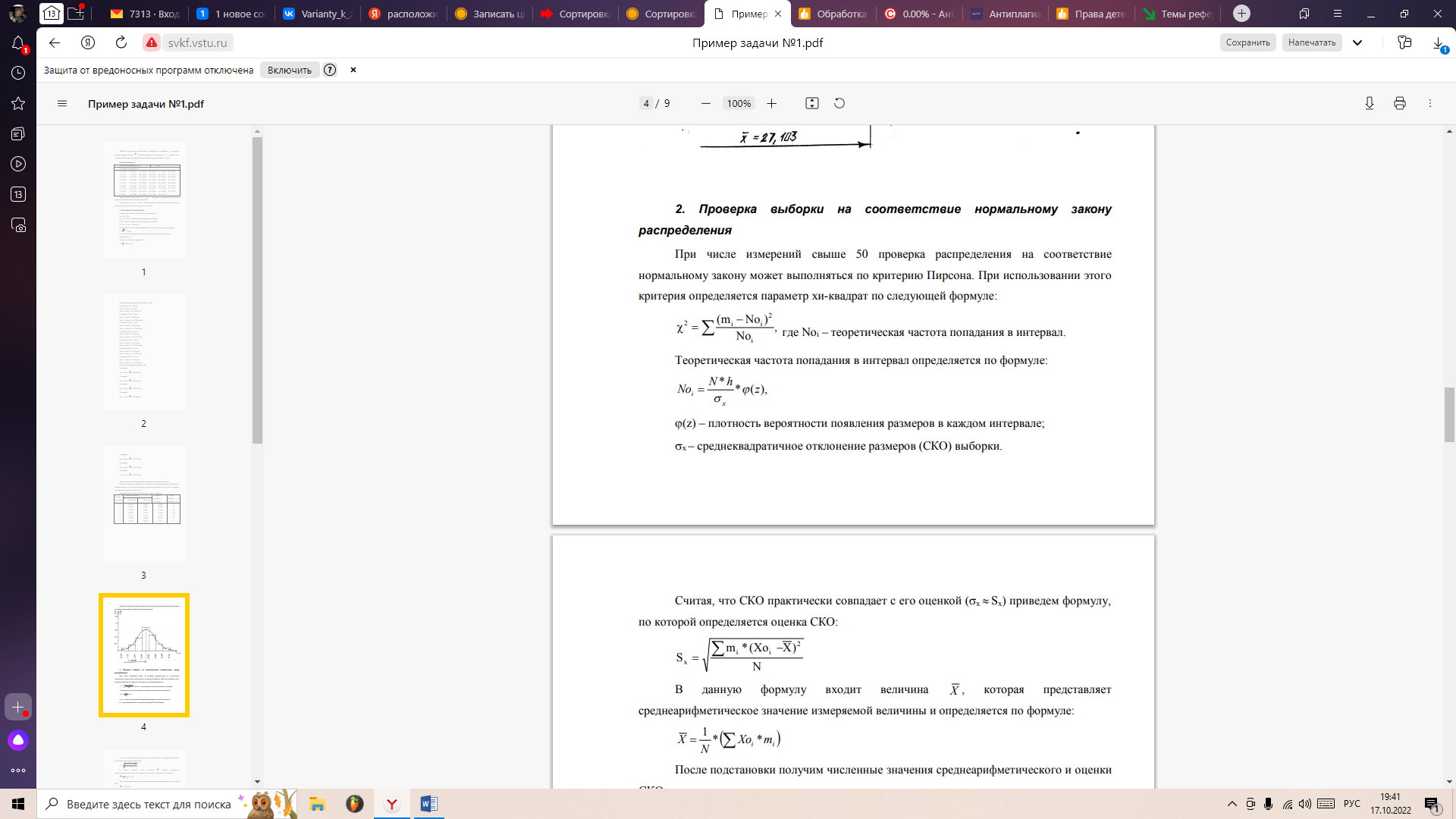где Noi – теоретическая частота попадания в интервал.
Теоретическая частота попадания в интервал определяется по формуле:



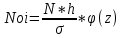
(z) – плотность вероятности появления размеров в каждом интервале;

x – среднеквадратичное отклонение размеров (СКО) выборки.

Считая, что СКО практически совпадает с его оценкой (x  Sx) приведем формулу, по которой определяется оценка СКО:



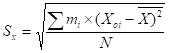
В данную формулу входит величина, которая представляет среднеарифметическое значение измеряемой величины и определяется по формуле:


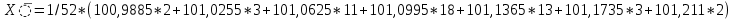= 101,10094 мм
После подстановки получим численные значения среднеарифметического и оценки СКО:

---

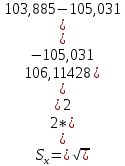
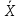=11,09615 мм

Sx  0,0472463 мм
Кроме полученных величин, для определения теоретической частоты попадания в интервал Noi необходимо знать плотность вероятности попадания размеров в каждом интервале. Эту величину можно определить по формуле:


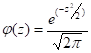
Так как расчеты по данной формуле достаточно сложны, значения плотности вероятности выбирают из таблицы в зависимости от безразмерного параметра Z, который для каждого интервала определяется по формуле:

Для 1 интервала:
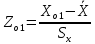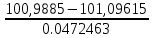= = -2,2784

что соответствует величине (z) = 0,0297
Для 2 интервала:
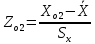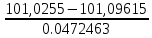= = - 1,4953

что соответствует величине (z) = 0,1304
Для 3 интервала:
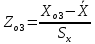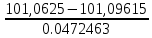= = - 0,7122

что соответствует величине (z) = 0,3809

Для 4 интервала:
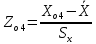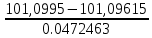= = 0,0709

что соответствует величине (z) = 0,397
Для 5 интервала:
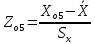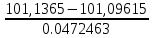= = 0,854

что соответствует величине (z) = 0,277
Для 6 интервала:
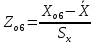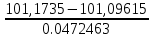= = 1,637

что соответствует величине (z) = 0,104
Для 7 интервала:
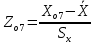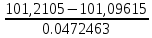= = 2,420

что соответствует величине (z) = 0,021
Определяем теоретические значения количества деталей для каждого интервала Noi.
Для 1 интервала:

---

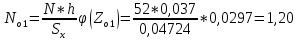
Для 2 интервала:

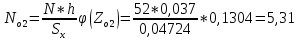
Для 3 интервала:

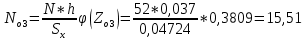
Для 4 интервала:

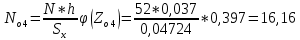
Для 5 интервала:

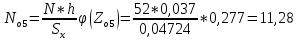
На основании результатов измерений и расчета теоретических данных определяем фактическую и теоретическую частоту попадания размеров в интервал:

№ интервала	Фактическая частота,	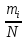Теоретическая частота,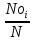
1	0,0384615	0,02307
2	0,0576923	0,10211
3	0,211538	0,29826
4	0,346154	0,31076
5	0,25	0,21692
6	0,0576923	0,08134
7	0,0384615	0,01634

Полученные результаты позволяют получить расчетную величину параметра хи-квадрат:







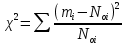
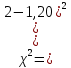
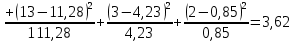
Для совпадения фактического закона распределения с теоретическим законом нормального распределения необходимо, чтобы выполнялось следующее условие:
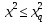
где 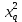– теоретическое граничное значение параметра хи-квадрат, которое определяется по таблице.
Для получения табличного значения необходимо определиться с двумя параметрами:
- уровнем значимости q, который показывает вероятность того, что законы не совпадут. В нашем случае, в соответствии с заданием, q = 0,05;

---

- числом степеней свободы , которое определяется в зависимости от числа интервалов n и числа определяемых по статистике параметров, необходимых для совмещения модели и гистограммы r. Для нормального закона распределения r = 2, так как закон однозначно характеризуется двумя параметрами – СКО и МО (математическим ожиданием). Число степеней свободы определяется по формуле:
 = n – 1 – r = 7 – 1 – 2 = 4
Таким образом, табличное значение = 9,48.
Так как выполняется неравенство 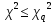, то можно сказать, что фактический закон распределения совпадает с теоретическим законом нормального распределения.
3. Определение доверительного интервала рассеивания случайных погрешностей вокруг среднего значения
Так как условие 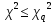выполняется, то гипотеза о совпадении экспериментального и выбранного теоретического (нормального) распределения принимается (она не противоречит данным).

Так как по условию Рд = 0,93, то значение функции Лапласа:

Ф(Zp) = Рд/2 = 0,465.

Определяем табл. величину нормированного параметра Zp, которая соответствует данному значению функции Лапласа

Zp = 1,81

Таким образом, доверительный интервал случайной ошибки:

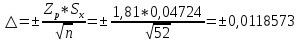мм

Постоянные неисключённые составляющие погрешности измерений:

 погрешность снятия показаний со шкалы (принимается равной 0,1 от цены деления шкалы прибора):



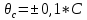
где С = 0,010 мм - цена деления шкалы прибора;



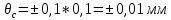
 систематическая неисключенная погрешность округления результата:





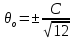
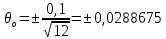
 неисключенная погрешность прибора (условно принимается равной цене деления шкалы прибора):

=

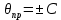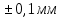
Суммирование частных постоянных погрешностей измерения производится по двум формулам:

---

Смотрите также файлы

• ыфв.docx

• Задания Определить оптимальный план перевозок с минимальными затратами для исходных данных, приведенных ниже.docx

• Социальные образы (мужчиныженщины) и их выбор для рекламного послания.docx

• Отчет по лабораторной работе по дисциплине Физика (наименование учебной дисциплины согласно учебному плану).docx

• Практическое задание 1 Запишите вид парной линейной регрессии. Дайте определение всем входящим в нее элементам.docx