Выполнить обработку результатов многократных прямых измерений
Таблица 1 – Исходные данные

	Номер варианта
	3
1	7,95
2	7,958
3	7,958
4	7,958
5	7,96
6	7,96
7	7,96
8	7,955
9	7,955
10	7,955
11	7,952
12	7,952
13	7,952
14	7,953
15	7,953
16	7,953
17	7,958
18	7,957
19	7,958
20	7,942
21	7,943
22	7,943
23	7,949
24	7,949
25	7,949
26	7,957
27	7,957
28	7,957
29	7,948
30	7,948
31	7,948
32	7,946
33	7,946
34	7,946

Выполнение
Сведений об известных систематических погрешностях нет.

Вычисляем среднее арифметическое результатов наблюдений по формуле:
, (1)
где

---

– результат i-го единичного измерения;

n – число единичных измерений в ряду.

Результат вычисления приведен на рисунке 1 в ячейке D2.

Вычисляем СКО – среднеквадратическое отклонение. Так как число измерений n=34>20, то используем формулу:
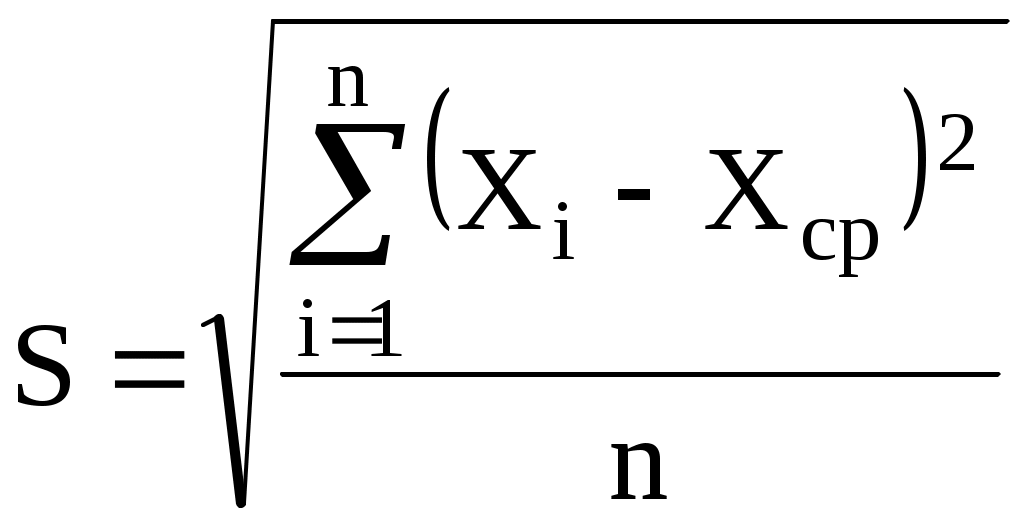. (2)
Результат вычисления приведен на рисунке 1 в ячейке D3.

Оценку случайной погрешности среднего арифметического значения результата измерений проводим путем вычисления среднего арифметического
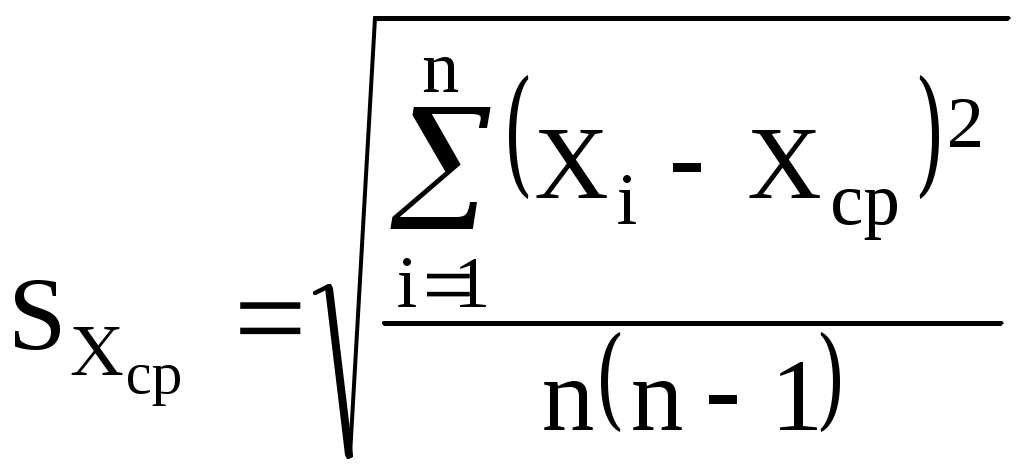. (3)
Результат вычисления приведен на рисунке 1 в ячейке D6.

Проверяем гипотезу о нормальности распределения результатов наблюдения. При числе результатов 15

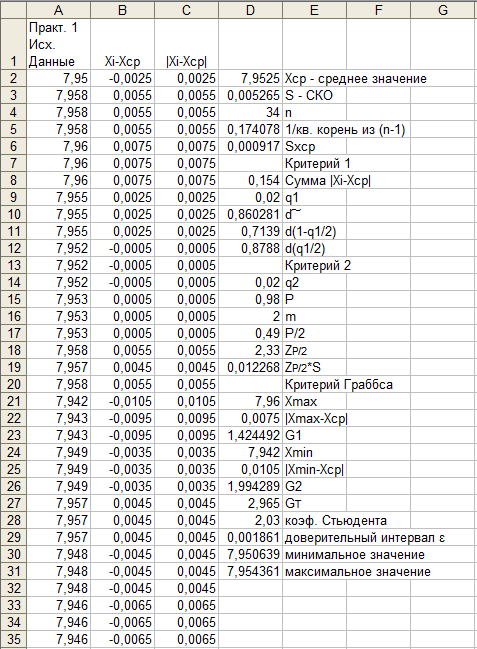
Рисунок 1 – Результаты вычислений
Критерий 1.

Вычисляем отношение:
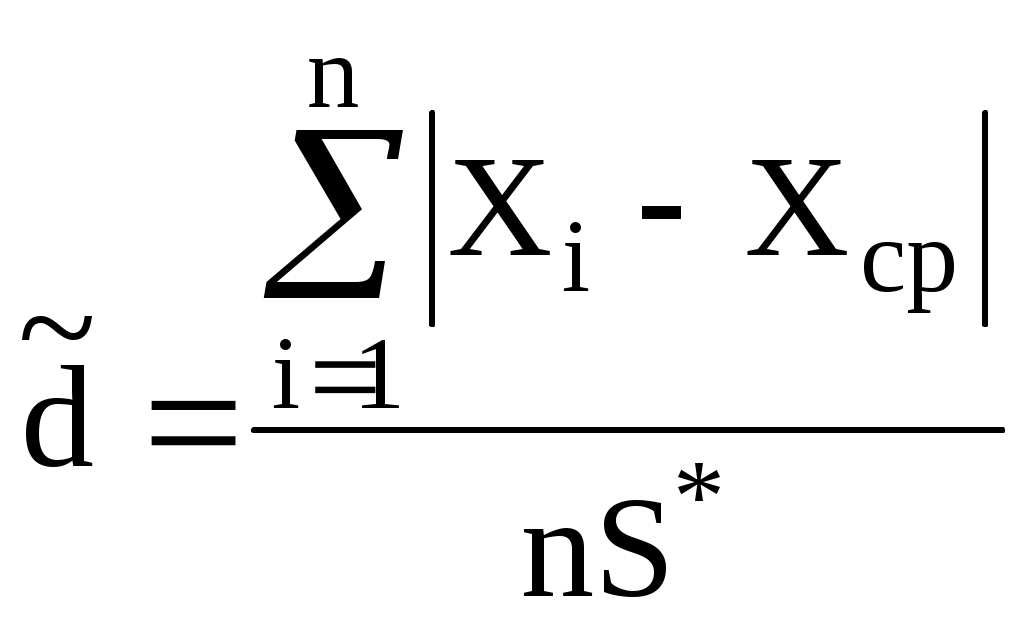, (4)
где – смещенное среднее квадратическое отклонение, вычисляемое по (2),

Вычисляем (столбец В1-В35 на рисунке 1).

Вычисляем (столбец С1-С35 на рисунке 1).

Вычисляем (ячейка D8 на рисунке 1).

Результат вычисления приведен на рисунке 1 в ячейке D10.

Результаты измерений в ряду считают распределенными нормально, если:
, (5)
где и квантили распределения, получаемые из таблицы Б.1 [1] по n,

---

и ( ).

Примем =0,02, тогда согласно таблице Б.1 [1] при n=34, =1 % и ( )=99 % получаем =0,7139 и =0,8788 (ячейки D11 и D12 соответственно на рисунке 1).

Как видно неравенство (5) выполняется . Это означает, что в соответствии с первым критерием (при уровне значимости =0,02) результаты измерений распределены по нормальному закону.

Критерий 2.

Считают, что результаты измерений принадлежат нормальному распределению, если не более m разностей удовлетворяют неравенству:
, (6)
где – верхний квантиль распределения нормированной функции Лапласа, отвечающий вероятности Р/2.

Значения вероятности Р определяют из таблицы Б.2 [1] по выбранному уровню значимости , и числу результатов измерений n, а зависимость от Р по таблице Б.3 [1].

Примем =0,02, тогда при n=34 согласно таблице Б.2 [1] Р=0,98, а m=2 (ячейки D15 и D16 соответственно на рисунке 1). По таблице Б.3 [1] определяем =2,33 (ячейка D18 на рисунке 1).

Результат вычисления приведен на рисунке 1 в ячейке D19.

Как видно неравенство (6) не выполняется ни разу, то есть ни одна разность

---

не превышает значения .

Таким образом, оба критерия говорят о том, что распределение результатов измерений с уровнем значимости 0,04 можно признать нормальным.

Определяем наличие грубых погрешностей и промахов по критерию Граббса (ГОСТ 8.736–2011 [1]). Для этого вычисляют критерии Граббса и , предполагая, что наибольший (ячейка D21 на рисунке 1) или наименьший (ячейка D24 на рисунке 1) результат измерений вызван грубыми погрешностями:
, (7)
. (8)
Вычисляем (ячейка D22 на рисунке 1).

Вычисляем (ячейка D25 на рисунке 1).

Результаты вычисления и приведены на рисунке 1 в ячейках D23 и D26 соответственно.

Теоретическое значение критерия Граббса при уровне значимости q=5 % определяем по таблице А.1 [1] (ячейка D27 на рисунке 1).

Если > , то исключают как маловероятное значение. Если >

---

, то исключают как маловероятное значение.

Поскольку < и < , то и не считаем промахами и сохраняем в ряду результатов измерений.

Определяем доверительные границы случайной погрешности ε по формуле:
, (9)
где – коэффициент распределения Стьюдента при заданной доверительной вероятности Р и числе наблюдений n, определяемый по таблице Д.1 [1].

При доверительной вероятности Р=0,95 и числе наблюдений n=34 по таблице Д.1 [1] определяем =2,03 (ячейка D28 на рисунке 1).

Результат вычисления приведен на рисунке 1 в ячейке D29.

Вычисленные минимальное и максимальное значения приведены на рисунке 1 в ячейках D30 и D31 соответственно.

Запишем результат измерения с учётом правил округления:
, Р=0,95.


Список литературы
1. ГОСТ 8.736–2011 Измерения прямые многократные. Методы обработки результатов измерений.

2. Сергеев, А. Г. Метрология, стандартизация и сертификация : учебник / А. Г. Сергеев, В. В. Терегеря. – М. : Издательство Юрайт ; ИД Юрайт, 2011. – 820 с. Серия : Основы наук.

3. Лифиц И.М. Стандартизация, метрология и сертификация: Учебник. – 5-е изд., перераб. и доп. – М. : Юрайт-Издат. 2005. – 345 с.

4. Метрология [Текст] : учебник для студентов технических специальностей / А. А. Брюховец [и др.] ; ред. С. А. Зайцев. - 2-е изд., перераб. и доп. – М. : ФОРУМ, 2011. – 464 с.50>

---

Смотрите также файлы

• Тест для определения темперамента Г. Ю. Айзенка.docx

• Выбытие (столбец 6) производственный и хозинвентарь 0,028 млн руб.docx

• Задание Ответьте на вопросы, обосновывая свой ответ Дайте понятие банковской деятельности. Назовите банковские операции и сделки.docx

• Задача 1 у альпиниста 27ми лет на высоте 5000 м над уровнем моря впервые во время сна изменился характер дыхания после нескольких глубоких дыхательных движений наступает остановка дыхания, за которой снова возникают глубокие дыхательные движения и т д..docx

• А. в этой связи оформите результаты своих размышлений в таблице.docx