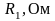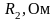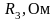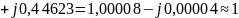Добавлен: 02.02.2019
Просмотров: 561
Скачиваний: 8
Некоммерческое акционерное общество
«АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ»
Кафедра теоретических основ электротехники

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №3
По дисциплине «Основы теории цепей»
На тему «Расчёт пассивных четырехполюсников»
Специальность «Информационные системы»
Выполнил Ануарбеков Шыңғыс Группа ИС-16-2
Принял доцент каф. ТОЭ Айтжанов Н.М.
_________ «____»____________201_г.
Алматы 201_
Содержание
Введение...................................................................................................................3
Параметры элементов четырехполюсника...........................................................4
Задание.....................................................................................................................5
Расчетная часть...................................................................................................6-12
Комплексные сопротивления четырехполюсников......................................6
А-параметры четырехполюсника...................................................................6
H-параметры четырехполюсника...................................................................8
Характеристические сопротивления ZC1 и ZC2............................................10
Характеристическая постоянная передачи ГC, характеристическое ослабление AC, фазовая постоянная BC.........................................................................11
Заключение.............................................................................................................13
Список литературы................................................................................................14
Введение
Цель работы: получение навыков исследования различных режимов работы пассивного симметричного четырёхполюсника и определение его параметров.
Расчет пассивных четырехполюсников. Заданы схемы четырехполюсников (см. рисунки 3.1-3.10). Параметры элементов четырехполюсника приведены в таблицах 3.1-3.3.
Таблица 3.1
|
Год поступления |
Первая буква фамилии |
|||||||||
|
Четный |
АБВ |
ГДЕ |
ЖЗИ |
КЛ |
МН |
ОПР |
СТУ |
ХФЦ |
ЧШЩ |
ЭЮЯ |
|
Нечетный |
ЭЮЯ |
ЧШЩ |
ХФЦ |
СТУ |
ОПР |
МН |
КЛ |
ЖЗИ |
ГДЕ |
АБВ |
|
№ схемы |
3.1 |
3.2 |
3.3 |
3.4 |
3.5 |
3.6 |
3.7 |
3.8 |
3.9 |
3.10 |
|
Параметры |
H |
Z |
Y |
H |
Z |
Y |
H |
Z |
Y |
H |
Таблица 3.2
|
Год поступления |
Последняя цифра студенческого билета |
|||||||||
|
Четный |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
Нечетный |
0 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
|
20 |
30 |
35 |
40 |
45 |
15 |
25 |
50 |
20 |
30 |
|
|
60 |
50 |
40 |
30 |
55 |
45 |
35 |
20 |
25 |
40 |
|
|
15 |
25 |
20 |
65 |
30 |
40 |
18 |
10 |
15 |
20 |
Таблица 3.3
|
Год поступления |
Предпоследняя цифра студенческого билета |
|||||||||
|
Четный |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Нечетный |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
XL1 |
40 |
45 |
20 |
30 |
25 |
30 |
40 |
60 |
15 |
20 |
|
XL2 |
50 |
30 |
25 |
20 |
40 |
35 |
20 |
45 |
30 |
50 |
|
XL3 |
30 |
20 |
40 |
35 |
25 |
15 |
28 |
36 |
45 |
35 |
|
XC1 |
35 |
80 |
60 |
50 |
30 |
20 |
25 |
40 |
55 |
45 |
|
XC2 |
20 |
25 |
30 |
40 |
20 |
10 |
35 |
20 |
50 |
30 |
|
XC3 |
50 |
40 |
20 |
30 |
10 |
35 |
15 |
20 |
25 |
10 |
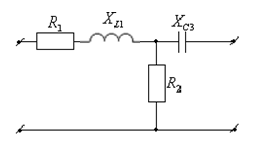
Рисунок 3.1
Задание:
1) Определить комплексные сопротивления четырехполюсника.
2) Определить А-параметры четырехполюсника, используя законы Кирхгофа и режимы холостого хода и короткого замыкания. Проверить выполнение соотношения А11 А22-А12А21=1.
3) Определить Z, Y или H – параметры четырехполюсника (согласно варианту).
4) Определить характеристические сопротивления ZC1 и ZC2 четырехполюсника, используя А-параметры и параметры холостого хода и короткого замыкания.
5) Определить характеристическую постоянную передачи ГC, характеристическое ослабление AC, фазовую постоянную BC четырехполюсника, используя А-параметры и параметры холостого хода и короткого замыкания.
Расчетная часть
1) Определить комплексные сопротивления четырехполюсника.
Составим схему замещения:
Рисунок 3.2
Из рисунка 3.1:
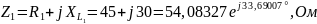
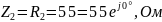
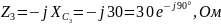
2) Определить А-параметры четырехполюсника, используя законы Кирхгофа и режимы холостого хода и короткого замыкания. Проверить выполнение соотношения А11 А22-А12А21=1.
Уравнения,
определяющие зависимость между
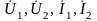 называются уравнениями передачи
четырёхполюсника. А-параметры
четырехполюсника определяются через
уравнения:
называются уравнениями передачи
четырёхполюсника. А-параметры
четырехполюсника определяются через
уравнения:
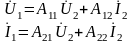 }
;
(1)
}
;
(1)
Параметры четырехполюсника являются комплексными величинами, определяются только схемой четырёхполюсника и её элементами; между различными системами параметров четырехполюсника существует однозначная связь.
Для пассивного четырёхполюсника:
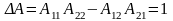 .
.
Запишем уравнения по законам Кирхгофа. По первому закону Кирхгофа алгебраическая сумма токов в узел схемы равна 0. Со знаком «+» записываются токи Iк, положительные направления которых направлены к рассматриваемому узлу, со знаком «-» записываются токи Iк, положительные направления которых направлены от данного узла (или наоборот). Запишем уравнение для узла a:
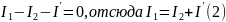
Второй закон Кирхгофа записывается для независимых контуров схемы, независимые контура выбираются так же, как и для цепей постоянного тока. Со знаком «+» записываются напряжения, если положительные направления токов Iк и направление обхода контура совпадают, в противном случае напряжения записываются со знаком «-». ЭДС Eк записываются со знаком «+», если положительные направления Eк и направление обхода контура совпадают. Запишем систему из двух уравнений для контуров, показанных на рисунке 3.2.
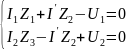 =>
=>
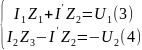
Из уравнения (4) имеем,
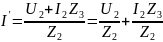
Подставляем в уравнение (2)
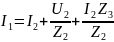
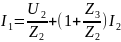
Тогда,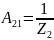 ,
,
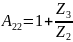
Из
3 уравнения имеем
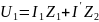 (7)
(7)
Подставляем (6) и (5) уравнения в (7):
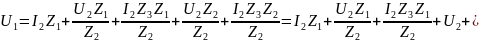
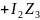
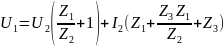
Тогда,
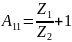 ,
,
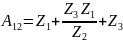 ,
следовательно
,
следовательно
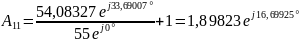
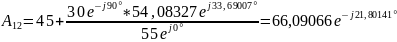
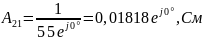
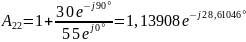
Проверим связь А-параметров:
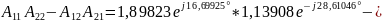
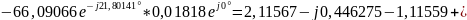
Найдем А-параметры, воспользовавшись режимом холостого хода и короткого замыкания:
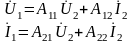 }
;
}
;
Обеспечим
холостой ход на выходе,
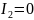
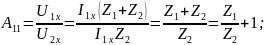
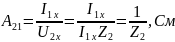
Обеспечим
короткое замыкание на выходе,
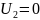
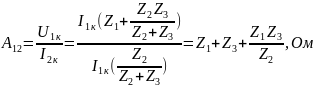
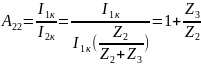
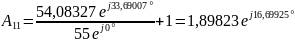
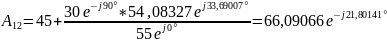
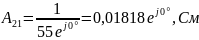
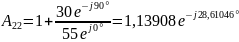
Проверим связь А-параметров:
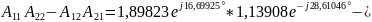
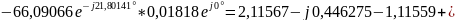
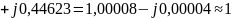
3) Определить Z, Y или H – параметры четырехполюсника (согласно варианту). По варианту необходимо определить H параметры:
Н-параметры четырехполюсника определяются через уравнения:
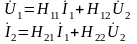 }
}
Н
– параметры:
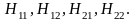 Для пассивного четырёхполюсника:
Для пассивного четырёхполюсника:
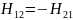
Для измерения Н-параметров четырехполюсника необходимо обеспечить режим холостого хода на входе и режим короткого замыкания на выходе.
Обеспечим
режим холостого хода на входе,
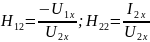
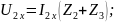
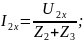
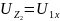
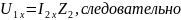
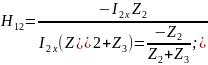
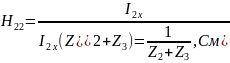
Обеспечим
короткое замыкание на выходе,
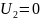
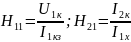
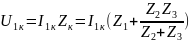
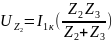
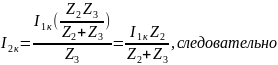
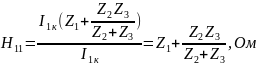
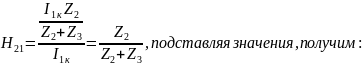
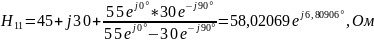
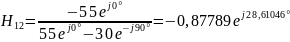
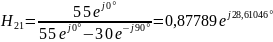
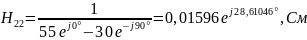
Н-параметры также можно выразить через А-параметры:
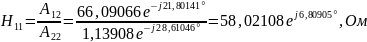
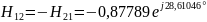
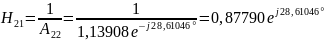
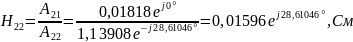
4) Определить характеристические сопротивления ZC1 и ZC2 четырехполюсника, используя А-параметры и параметры холостого хода и короткого замыкания.
Характеристическое
сопротивление ![]() равно
такому сопротивлению приемника
равно
такому сопротивлению приемника ![]() ,
подключенного к вторичным выводам, при
котором входное сопротивление со стороны
первичных выводов равно
,
подключенного к вторичным выводам, при
котором входное сопротивление со стороны
первичных выводов равно ![]() (рис.
3.3, а). Короче говоря, при
(рис.
3.3, а). Короче говоря, при ![]() имеем
имеем ![]() .
Аналогично при обратном питании и
сопротивлении приемника на первичных
выводах
.
Аналогично при обратном питании и
сопротивлении приемника на первичных
выводах ![]() получим
получим ![]() (рис. 3.3, б).
(рис. 3.3, б).
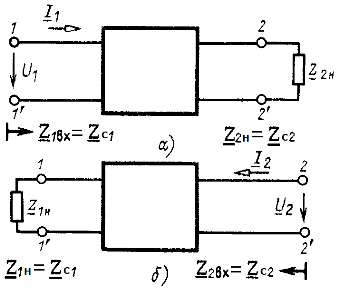
Рисунок 3.3
Характеристические сопротивления:
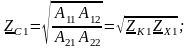
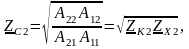
где
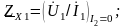
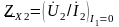 ;
;
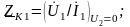
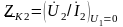 -
параметры холостого хода (х.х.) и короткого
замыкания (к.з.).
-
параметры холостого хода (х.х.) и короткого
замыкания (к.з.).
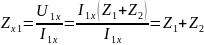
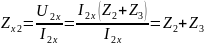
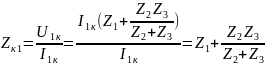
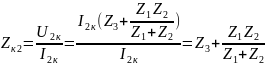
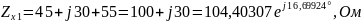
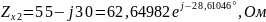
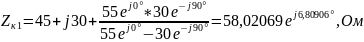
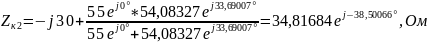
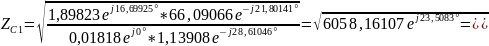
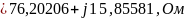
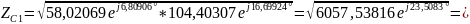
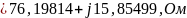
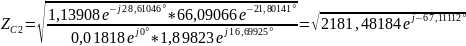
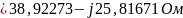
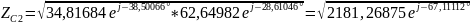
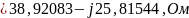
5) Определить характеристическую постоянную передачи ГC, характеристическое ослабление AC, фазовую постоянную BC четырехполюсника, используя А-параметры и параметры холостого хода и короткого замыкания.
Характеристическая постоянная передачи:
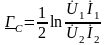 .
.
Характеристическую постоянную передачи можно выразить через А-параметры и параметры холостого хода и короткого замыкания:
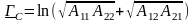 ,
,
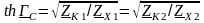 .
.
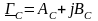 ,
где
,
где
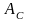 – характеристическое ослабление
четырёхполюсника:
– характеристическое ослабление
четырёхполюсника:
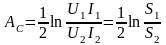 ,
единица измерения
,
единица измерения
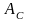 в масштабе натуральных логарифмов
называется непером (Нп). На практике
принято измерять
в масштабе натуральных логарифмов
называется непером (Нп). На практике
принято измерять
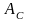 в децибелах (дБ);
в децибелах (дБ);
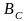 – фазовая
постоянная четырёхполюсника,
измеряется
в радианах или градусах:
– фазовая
постоянная четырёхполюсника,
измеряется
в радианах или градусах:
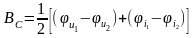 .
.
Выразим постоянную передачи через А-параметры:
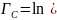
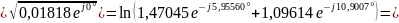
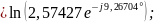
По
определению,
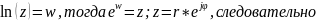
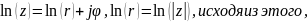
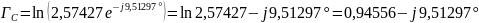
тогда
AC=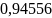 дБ,
BC=
дБ,
BC=
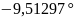 ;
;
Выразим постоянную передачи через режимы холостого хода и короткого замыкания:
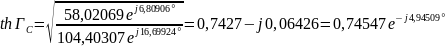
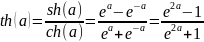
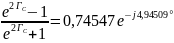
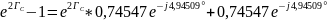
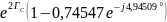 =
=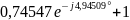
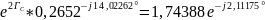
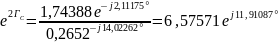
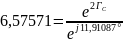
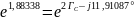
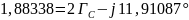
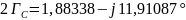
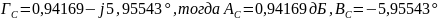
Заключение
В результате расчетно-графической работы были выполнены поставленные цели: получение навыков исследования различных режимов работы пассивного симметричного четырёхполюсника и определение его параметров. Были рассчитаны А-параметры четырехполюсника при помощи законов Кирхгофа и режимом холостого хода и короткого замыкания, также были рассчитаны Н-параметры четырехполюсника при помощи режимом холостого хода и короткого замыкания, определены характеристические сопротивления, характеристическая постоянная передачи, характеристическое ослабление и фазовая постоянная.
1. Жолдыбаева З.И., Надиров Е.Г. Основы теории цепей. Методические указания и задания по выполнению расчетно-графических работ №1-3 для студентов специальности 5B070300. – Алматы: АУЭС, 2014.
2. Жолдыбаева З.И., Коровченко Т.И. Теория электрических цепей 1: Конспект лекций. – Алматы, АИЭС, 2007.
3. Зевеке Г.В., Ионкин П.А. Основы теории цепей. Учебник для вузов. – М: «Энергия», 1975.