Файл: Контрольная работа По дисциплине Физика (часть1) Перфильев С. Е. Группа мбт22 Вариант 6 Новосибирск, 2022 г.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 81
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
= 10311,111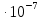
 1,03
1,03  (Тл)
(Тл)
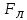 = 1,6
= 1,6 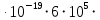 1,03
1,03  = 9,888
= 9,888 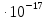
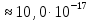 (Н)
(Н)
Ответ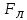 =
= 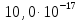 (Н)
(Н)
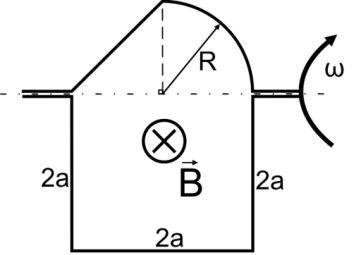
Рис.2
Дано
r = a
2а= 0,27 м
ω=3π рад/с
B=0,2 Тл
t=0
Фмак
t = 0,3 с
Rk=17 Ом
Найти
q - ?
Решение
Заряд связан с силой тока соотношением I =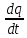 , q =
, q = 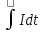
1. Магнитный поток через контур (максимальный)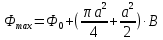 , где
, где 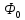 – поток через прямоугольную часть контура, а
– поток через прямоугольную часть контура, а 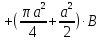 – поток через площадь, ограниченную четверть окружностью и прямоугольным треугольником
– поток через площадь, ограниченную четверть окружностью и прямоугольным треугольником
2.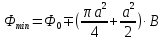
3. В любой момент времени
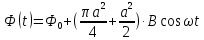
,
т.к.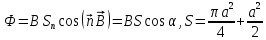 ,
,
где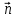 нормаль к поверхности контура. Угол
нормаль к поверхности контура. Угол 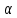 между
между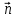 и
и 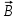 будет меняться по линейному закону:
будет меняться по линейному закону: 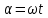
4. ЭДС индукции равна:
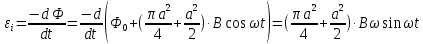 .
.
5. Индукционный ток равен: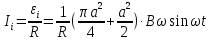 .
.
q =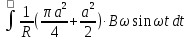
q = -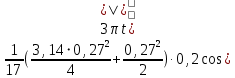
q = -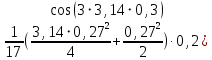 -
- 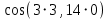 )
)
q = -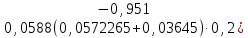 - 1) = 2,18234
- 1) = 2,18234 
Ответ: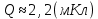
Дано
N = 12,5
t = 5 c
c
T = 1 c
c
Найти
β - ?
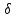 - ?
- ?
Решение
Для колебаний заряда в электрическом контуре, содержащем R, L, C, дифференциальное уравнение имеет вид:

здесь β - коэффициент затухания.
Время релаксации - это время, в течении которого амплитудное значение уменьшается в е раз.
- это время, в течении которого амплитудное значение уменьшается в е раз.
амплитудное значение заряда

1/2,72 = exp (-βτ), согласно условию τ = Т N
ln 2,72 = βτ
β =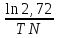 =
=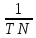
β =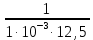 = 80 (c-1)
= 80 (c-1)
Определим относи́тельное измене́ние энергии контура за время, равное 5 мс — безразмерную величина, число, показывающее во сколько раз изменилась энергия контура относительно первоначального её значения.
Полная энергия контура в любой момент времени определяется по формуле: , в начальный момент времени t=0 энергия будет равна
, в начальный момент времени t=0 энергия будет равна  , тогда
, тогда
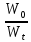 = exp (2βt)
= exp (2βt)
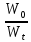 = exp (2
= exp (2  5
5  ) = 2,22666
) = 2,22666  2,2
2,2
Энергия контура уменьшилась в =
= 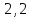
Ответ: β = 80 (c-1), =
= 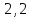
Х = 10 Cos (4 t ) Cos ( 104 t ),мм.
Cos ( 104 t ),мм.
Определить частоты складываемых колебаний и записать уравнения этих колебаний. Сколько колебаний совершает колеблющаяся точка за время, равное периоду биений?
Дано
Х = 10 Cos (4 t ) Cos ( 104 t ),мм
Cos ( 104 t ),мм
Найти
ω1 - ?
ω2 - ?
х1 - ?
х2 - ?
N - ?
Решение
В случае, когда складываемые колебания происходят по законам и
и  с небольшой разностью частот
с небольшой разностью частот  (или
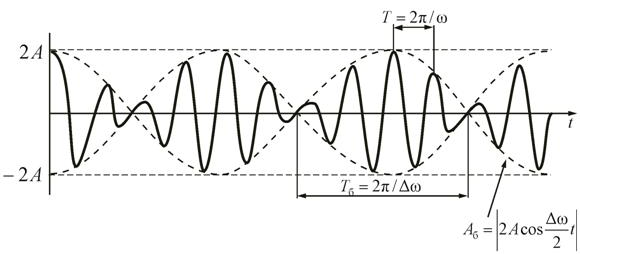
(или  ) возникают биения. Результирующее колебание описывается уравнением
) возникают биения. Результирующее колебание описывается уравнением


в котором выражение является амплитудой биений. Частота колебаний равна среднему арифметическому частот складываемых колебаний.
является амплитудой биений. Частота колебаний равна среднему арифметическому частот складываемых колебаний.
 - разность частот складываемых колебаний, следовательно, при биениях амплитуда меняется по гармоническому закону с частотой биений
- разность частот складываемых колебаний, следовательно, при биениях амплитуда меняется по гармоническому закону с частотой биений  .
.
Период биений равен
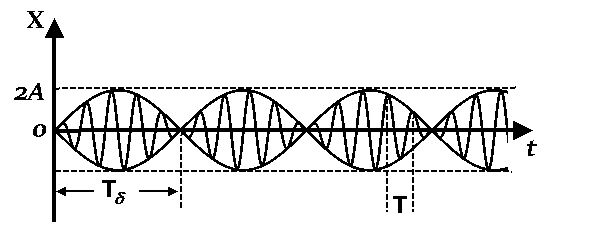
Согласно условию Х = 10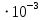 Cos (4 t )
Cos (4 t ) Cos ( 104 t ),м
Cos ( 104 t ),м
А = 10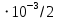 = 5
= 5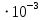 (м),
(м), 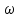 = 104 с-1
= 104 с-1
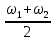 = 104
= 104
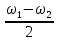 = 4 решим получившуюся систему
= 4 решим получившуюся систему
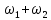 = 208
= 208
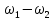 = 8, отсюда 2
= 8, отсюда 2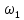
= 216,
 = 216/2 = 108 с-1
= 216/2 = 108 с-1
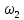 = 108 – 8 = 100 с-1
= 108 – 8 = 100 с-1
частота биений = 108 – 100 = 8 с-1
= 108 – 100 = 8 с-1
Период биений равен Тб =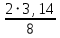 = 0,785 (с)
= 0,785 (с)
запишем законы колебаний
 и
и 
х1 = 5 cos (108t)
cos (108t)
х2 = 5 cos (100t)
cos (100t)
N =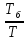 =
= 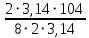 = 13
= 13
Ответ: N = 13, х1 = 5 cos (108t),
cos (108t),  = 108 с-1
= 108 с-1
х2 = 5 cos (100t),
cos (100t), 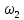 = 100 с-1
= 100 с-1
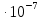
 1,03
1,03  (Тл)
(Тл)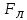 = 1,6
= 1,6 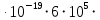 1,03
1,03  = 9,888
= 9,888 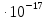
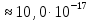 (Н)
(Н)Ответ
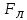 =
= 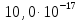 (Н)
(Н)-
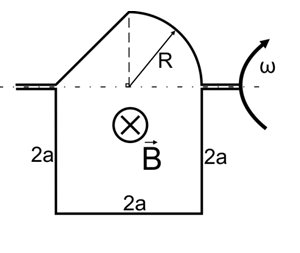
Контур находится в однородном магнитном поле с индукцией B=0,2 Тл. Верхнюю подвижную часть контура – провод изогнутый, как показано на рисунке 2 (радиус закругления равен а), вращают с постоянной угловой скоростью ω=3π рад/с вокруг оси ОО’. Длина стороны нижнего неподвижного контура составляет 27 см (2а=27 см). В момент времени t=0 магнитный поток через контур максимальный. Найти заряд, прошедший по контуру за 0,3 с от начального момента времени, если его сопротивление Rk=17 Ом.

Рис.2
Дано
r = a
2а= 0,27 м
ω=3π рад/с
B=0,2 Тл
t=0
Фмак
t = 0,3 с
Rk=17 Ом
Найти
q - ?
Решение
Заряд связан с силой тока соотношением I =
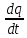 , q =
, q = 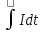

1. Магнитный поток через контур (максимальный)
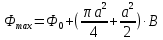 , где
, где 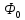 – поток через прямоугольную часть контура, а
– поток через прямоугольную часть контура, а 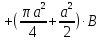 – поток через площадь, ограниченную четверть окружностью и прямоугольным треугольником
– поток через площадь, ограниченную четверть окружностью и прямоугольным треугольником 2.
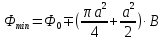
3. В любой момент времени
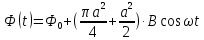
,
т.к.
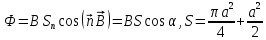 ,
,где
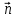 нормаль к поверхности контура. Угол
нормаль к поверхности контура. Угол 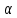 между
между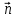 и
и 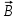 будет меняться по линейному закону:
будет меняться по линейному закону: 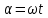
4. ЭДС индукции равна:
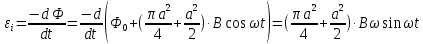 .
.5. Индукционный ток равен:
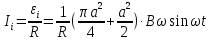 .
.q =
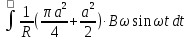
q = -
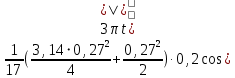
q = -
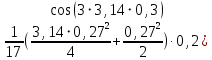 -
- 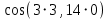 )
) q = -
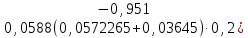 - 1) = 2,18234
- 1) = 2,18234 
Ответ:
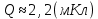
-
За время релаксации в колебательном контуре совершается 12,5 колебаний. Определить коэффициент затухания и относительное изменение энергии контура за время, равное 5 мс. Период колебаний в контуре равен 1 мс.
Дано
N = 12,5
t = 5
 c
cT = 1
 c
cНайти
β - ?
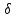 - ?
- ?Решение
Для колебаний заряда в электрическом контуре, содержащем R, L, C, дифференциальное уравнение имеет вид:
здесь β - коэффициент затухания.
Время релаксации
амплитудное значение заряда
1/2,72 = exp (-βτ), согласно условию τ = Т N
ln 2,72 = βτ
β =
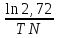 =
=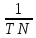
β =
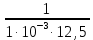 = 80 (c-1)
= 80 (c-1)Определим относи́тельное измене́ние энергии контура за время, равное 5 мс — безразмерную величина, число, показывающее во сколько раз изменилась энергия контура относительно первоначального её значения.
Полная энергия контура в любой момент времени определяется по формуле:
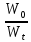 = exp (2βt)
= exp (2βt)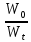 = exp (2
= exp (2 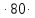 5
5  ) = 2,22666
) = 2,22666  2,2
2,2Энергия контура уменьшилась в
 =
= 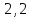
Ответ: β = 80 (c-1),
 =
= 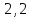
-
При сложении гармонических колебаний с близкими частотами уравнение результирующего колебания имеет вид:
Х = 10 Cos (4 t )
 Cos ( 104 t ),мм.
Cos ( 104 t ),мм.Определить частоты складываемых колебаний и записать уравнения этих колебаний. Сколько колебаний совершает колеблющаяся точка за время, равное периоду биений?
Дано
Х = 10 Cos (4 t )
 Cos ( 104 t ),мм
Cos ( 104 t ),мм
Найти
ω1 - ?
ω2 - ?
х1 - ?
х2 - ?
N - ?
Решение
В случае, когда складываемые колебания происходят по законам
в котором выражение
Период биений равен

Согласно условию Х = 10
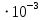 Cos (4 t )
Cos (4 t ) Cos ( 104 t ),м
Cos ( 104 t ),мА = 10
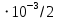 = 5
= 5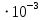 (м),
(м), 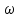 = 104 с-1
= 104 с-1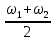 = 104
= 104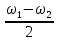 = 4 решим получившуюся систему
= 4 решим получившуюся систему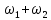 = 208
= 208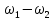 = 8, отсюда 2
= 8, отсюда 2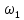
= 216,
 = 216/2 = 108 с-1
= 216/2 = 108 с-1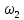 = 108 – 8 = 100 с-1
= 108 – 8 = 100 с-1частота биений
Период биений равен Тб =
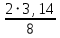 = 0,785 (с)
= 0,785 (с)запишем законы колебаний
х1 = 5
 cos (108t)
cos (108t)х2 = 5
 cos (100t)
cos (100t)
N =
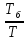 =
= 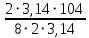 = 13
= 13Ответ: N = 13, х1 = 5
 cos (108t),
cos (108t),  = 108 с-1
= 108 с-1х2 = 5
 cos (100t),
cos (100t), 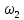 = 100 с-1
= 100 с-1