Файл: Лабораторная работа Задачи конструирования работа не принята. 0,2 за выбор задачи, но не за работу с ней задания 15 не рассматриваю как заимствованные со всей дурью их выполнения..docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 143
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, имеющей форму квадрата со стороной 500 пикселей. В начальный момент времени Черепаха находится в центре арены, ее голова направлена к верхней стороне квадрата, хвост опущен. Черепаха может выполнять команды:
При опущенном хвосте Черепаха оставляет на арене след в виде линии.
С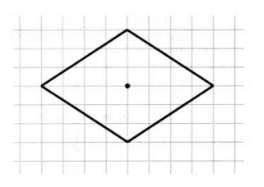
оставьте алгоритм в словесно-пошаговой форме для Черепахи таким образом, чтобы в результате его выполнения в центре арены появился ромб, представленный на рисунке, а Черепаха вернулась в исходное положение. [из заданий ОГЭ]
Анализ данной задачи представлен в таблице 2.
Таблица 2 – Анализ задачи на разработку модели процесса
Задать язык и среду исполнения можно коротко, указав только названия, подразумевая, что решатель легко восстановит все необходимые сведения самостоятельно. Так уместно поступать, если продолжительное время идет работа с одним и тем же языком, например, с алгоритмическм языком, или с одним и тем же исполнителем, например, с Лого-черепашкой. Если встреча с языком и исполнителем эпизодическая в ряду многих примеров, то при анализе формулировки требуется некоторая детализация описания, в разумной степени подробности. Если язык жестко связан с устройством исполнителя, то среда описывается как исполнитель: среда его обитания, необходимая часть системы команд и условия их безотказного выполнения. Язык в такой ситуации, как правило, является специфическим, следовательно, требует пояснений (см. таб. 3, примеры КФ2 и КФ3).
Таблица 3.
Примеры анализа задач на разработку модели процесса
Варианты формулирования. По заданности или незаданности в формулировке того или иного компонента задачной ситуации можно наблюдать варианты формулировок вокруг одной задачной ситуации (или аналогичных ситуаций). Использование в процессе обучения разных вариантов, в идеале - полный перебор всех вариантов, обеспечивает тренировку умственных действий, необходимых для задач этого класса и разнообразит контроль.
Количество таких вариантов конечно. Формально каждый компонент формулировки, кроме требования, может быть задан или не задан. Таких компонентов 5 (Язык, Среда, Ограничения, Старт, Цель/Модель) следовательно, формальный перебор даст 25= 32 вариантов, в которых могут быть не заданы 1, 2, 3, 4 или все 5 компонентов. Содержательный анализ комбинаций позволяет существенно уменьшить количество формальных вариаций до приемлемого множества «рабочих» вариантов. Рассуждения для задач на разработку модели и для заданий требуется разделить (для заданий они будут приведены несколько дальше).
Так если в формулировках задач на разработку модели процесса не заданы одновременно, ни стартовые позиции, ни цель, то задачная система не задана вовсе. Задачная система существует, как только заданы её базовые компоненты: объявлено требование (Модель процесса), указаны Стартовые позиции и Цель. Оставшиеся три компонента (Язык, Среда, Ограничения) при таких общих условиях дают только 8 вариантов. Те из них, где что-то (кроме Ограничений) не задано, можно рассматривать как формулировки с не полной, но достаточной для додумывания информацией при условии, что множество языков, которые могут использовать учащиеся, все-таки ограничено.
Если, все-таки, не заданы Стартовые позиции, то каждый такой вариант формулировки есть задача на подбор множества исходных состояний объекта, из которых можно прийти к заданному конечному его состоянию, и описание процесса какого-либо из таких переходов. Если не задана Цель, то каждый вариант такой формулировки рассматривается как задача на определение множества допустимых преобразований объекта из стартового состояния, выбор какого-либо из таких переходов и его описание. Можно сказать, что это задачи на усмотрение задачной ситуации и определение задачной системы (
составление задачи на моделирование процесса на основе некоторого ориентира).
Очевидно, что конкретных решений для задач последних двух групп не существует. Неконкретность области поиска позволяет отнести такие задачи к полуэвристическим или даже творческим. При этом в каждой из последних рассмотренных групп возможны варианты перебора других компонентов, позволяющие внутри групп варьировать сложность непростых по определению творческих задач. Такие задачи используются, главным образом, в олимпиадах.
Возможности варьирования в формулировках заданных/не заданных второстепенных компонентов задачной системы покажем на нескольких вариантах формулировок задач (см. таб. 4) по одной и той же задачной системе для Чертежника (см. таб. 3, пример КФ3). Курсивом в графе «интерпретация варианта» акцентировано дополнительное затруднение решателю, задаваемое такой формулировкой.
Таблица 4
Варианты формулировок задач на разработку модели процесса для Чертежника
Примером формулировки, в которой не указаны стартовые позиции (задачи на подбор множества исходных состояний объекта, из которых можно прийти к заданному конечному его состоянию), может быть следующая: «Разработать программу для Чертежника, в результате которой будет изображена фигура (дан чертёж фигуры на координатной плоскости, например «пятиконечная звезда», «раскрытый конверт»). Подобрать такое исходное положение чертежника, чтобы фигуру можно было нарисовать, не поднимая пера и не проходя дважды по одной и той же линии».
В качестве примера формулировки, в которой не конкретизировано конечное состояние (цель), т.е. в качестве примера задачи на усмотрение задачной ситуации и определение задачной системы (= составление задачи на моделирование процесса на основе некоторого ориентира) предлагаем такую формулировку: «Задана конкретная обстановка для Робота (КУМир) (дан рисунок поля, на котором есть лабиринт из стен, а некоторые клетки в лабиринте радиоактивны). Составьте задачу на разработку программы для Робота и решите её».
Обращение задач на моделирование процесса
Если в системе задачи на разработку модели процесса сама модель дана и требуется определить какую-либо деталь процесса ее создания, не реализуя при этом смоделированный процесс, а только изучая его описание, то группа таких формулировок-вопросов рассматривается как взаимообратные. При этом прямой задачей всегда будет являться та, в которой модель объявлена требованием, а обратные задачи будут отличаться по типу от прямой, т. е. по сути, являются качественными задачами-вопросами. Поэтому таблицу 2 можно продолжить, добавив в нее обратные качественные задачи-вопросы. При этом мы видим, что то, что было требованием (модель процесса), становится базисом или основой для данных задач. Формулировки обратных задач представлены в таблице 5.
Таблица 5 – Сопоставление взаимообратных задач на разработку модели процесса
-
поднять хвост -
опустить хвост -
вперед (n) – Черепаха перемещается на n шагов в том направлении, куда развернута ее голова; один шаг перемещения Черепахи соответствует одному пикселю; -
вправо (m) – Черепаха изменяет направление движения на m градусов по часовой стрелке.
При опущенном хвосте Черепаха оставляет на арене след в виде линии.
С
оставьте алгоритм в словесно-пошаговой форме для Черепахи таким образом, чтобы в результате его выполнения в центре арены появился ромб, представленный на рисунке, а Черепаха вернулась в исходное положение. [из заданий ОГЭ]Анализ данной задачи представлен в таблице 2.
Таблица 2 – Анализ задачи на разработку модели процесса
| КФ задачи | Д  ано описание исполнителя «Черепаха» (…). Составьте алгоритм для Черепахи таким образом, чтобы в результате его выполнения в центре арены появился ромб, представленный на рисунке. | |||||
| Базис | Условие | Условие | Условие | Требование | ||
| Структура задачной системы | Язык: | Среда: | Ограни чения: | Стартовые позиции: | Описание конечного объекта | Модель процесса |
| Словесно-пошаговая запись | Исполнитель Черепаха действует на песчаной арене, имеющей форму квадрата со стороной 500 пикселей. СКИ: вперед (n), вправо (m), поднять хвост опустить хвост | квадрат со стороной 500 пикселей | Черепаха находится в центре арены, ее голова направлена к верхней стороне квадрата, хвост опущен | | поднять хвост вперед (30) опустить хвост вправо (135) вперед (50) вправо (135) вперед (50) вправо (135) вперед (50) вправо (135) вперед (50) вправо (90) поднять хвост вперед (30) вправо (180) опустить хвост | |
| Изображен ромб в центре арены, представлен-ный на рисунке, Черепаха находится в центре арены, ее голова направлена к верхней стороне квадрата, хвост опущен | ||||||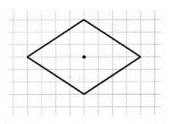
Задать язык и среду исполнения можно коротко, указав только названия, подразумевая, что решатель легко восстановит все необходимые сведения самостоятельно. Так уместно поступать, если продолжительное время идет работа с одним и тем же языком, например, с алгоритмическм языком, или с одним и тем же исполнителем, например, с Лого-черепашкой. Если встреча с языком и исполнителем эпизодическая в ряду многих примеров, то при анализе формулировки требуется некоторая детализация описания, в разумной степени подробности. Если язык жестко связан с устройством исполнителя, то среда описывается как исполнитель: среда его обитания, необходимая часть системы команд и условия их безотказного выполнения. Язык в такой ситуации, как правило, является специфическим, следовательно, требует пояснений (см. таб. 3, примеры КФ2 и КФ3).
Таблица 3.
Примеры анализа задач на разработку модели процесса
| Стр. ЗС | Базис | Условие | Требов-е | |||||||||
| Язык | Среда | Ограничения | Стартовые позиции | Цель | Модель процесса | |||||||
| КФ 2 | На информационной ленте машины Поста на некотором расстоянии от каретки, стоящей над пустой клеткой, находится непрерывный массив меток. Требуется присоединить к правому концу массива одну метку. [70, с.74] | |||||||||||
| Структура команды: n K m, где n – порядковый номер команды, K – действие, выполняемое кареткой, m – номер следующей команды, подлежащей выполнению. Пример п-мы: 1 ← 2 2 ? 3, 1 3! | Машина Поста. | нет | Состояние машины Поста: на ленте на некотором расстоянии от каретки, стоящей над пустой клеткой, находится непрерывный массив меток | К правому концу массива присоединена одна метка. | Текст программы | |||||||
| Клетки на бесконечной неподвижной ленте, читающе-пишущая подвижная каретка. Команды: nm - сдвиг влево; nm - сдвиг вправо; nm - запись метки в пустую клетку; n↨m - стирание метки в текущей клетке; n! - стоп; n ? m,k - если текущая клетка пустая, выполни команду с номером m, иначе - с номером k. | ||||||||||||
| КФ 3 | Напишите для Чертежника последовательность команд, по которой он изобразит треугольник, положение вершин которого на координатной плоскости определяется парами чисел (1,1), (3,5), (5,2). При этом число команд не должно превышать число пять. Рассмотрите несколько вариантов выполнения. | |||||||||||
| Определяется по исполнителю: построчная запись последовательности команд | Исполнитель Чертежник. Среда - координатная плоскость. СК: Опусти перо; Подними перо; Переведи в точку (x, y) | Число команд не должно превышать пяти | Чертежник в начале координат, перо поднято | На координатной плоскости изображен треугольник, положение вершин которого определяется парами чисел (1,1), (3,5), (5,2) | Варианты последовательностей команд | |||||||
Варианты формулирования. По заданности или незаданности в формулировке того или иного компонента задачной ситуации можно наблюдать варианты формулировок вокруг одной задачной ситуации (или аналогичных ситуаций). Использование в процессе обучения разных вариантов, в идеале - полный перебор всех вариантов, обеспечивает тренировку умственных действий, необходимых для задач этого класса и разнообразит контроль.
Количество таких вариантов конечно. Формально каждый компонент формулировки, кроме требования, может быть задан или не задан. Таких компонентов 5 (Язык, Среда, Ограничения, Старт, Цель/Модель) следовательно, формальный перебор даст 25= 32 вариантов, в которых могут быть не заданы 1, 2, 3, 4 или все 5 компонентов. Содержательный анализ комбинаций позволяет существенно уменьшить количество формальных вариаций до приемлемого множества «рабочих» вариантов. Рассуждения для задач на разработку модели и для заданий требуется разделить (для заданий они будут приведены несколько дальше).
Так если в формулировках задач на разработку модели процесса не заданы одновременно, ни стартовые позиции, ни цель, то задачная система не задана вовсе. Задачная система существует, как только заданы её базовые компоненты: объявлено требование (Модель процесса), указаны Стартовые позиции и Цель. Оставшиеся три компонента (Язык, Среда, Ограничения) при таких общих условиях дают только 8 вариантов. Те из них, где что-то (кроме Ограничений) не задано, можно рассматривать как формулировки с не полной, но достаточной для додумывания информацией при условии, что множество языков, которые могут использовать учащиеся, все-таки ограничено.
Если, все-таки, не заданы Стартовые позиции, то каждый такой вариант формулировки есть задача на подбор множества исходных состояний объекта, из которых можно прийти к заданному конечному его состоянию, и описание процесса какого-либо из таких переходов. Если не задана Цель, то каждый вариант такой формулировки рассматривается как задача на определение множества допустимых преобразований объекта из стартового состояния, выбор какого-либо из таких переходов и его описание. Можно сказать, что это задачи на усмотрение задачной ситуации и определение задачной системы (
составление задачи на моделирование процесса на основе некоторого ориентира).
Очевидно, что конкретных решений для задач последних двух групп не существует. Неконкретность области поиска позволяет отнести такие задачи к полуэвристическим или даже творческим. При этом в каждой из последних рассмотренных групп возможны варианты перебора других компонентов, позволяющие внутри групп варьировать сложность непростых по определению творческих задач. Такие задачи используются, главным образом, в олимпиадах.
Возможности варьирования в формулировках заданных/не заданных второстепенных компонентов задачной системы покажем на нескольких вариантах формулировок задач (см. таб. 4) по одной и той же задачной системе для Чертежника (см. таб. 3, пример КФ3). Курсивом в графе «интерпретация варианта» акцентировано дополнительное затруднение решателю, задаваемое такой формулировкой.
Таблица 4
Варианты формулировок задач на разработку модели процесса для Чертежника
| № | Конкретная формулировка | Интерпретация варианта формулировки |
| 1 | Напишите для Чертежника последовательность из записанных построчно пяти команд, по которой он изобразит треугольник, положение вершин которого на координатной плоскости определяется парами чисел (1,1), (3,5), (5,2). В исходном состоянии Чертежник находится в начале координат с поднятым пером. Используйте команды «опусти перо» и «переведи в точку (x, y)» . | Явно заданы все компоненты задачной системы, включая ограничения на описание процесса |
| 2 | Напишите на языке исполнителя «Чертежник» последовательность команд, по которой он изобразит треугольник, положение вершин которого на координатной плоскости определяется парами чисел (1,1), (3,5), (5,2). В исходном состоянии Чертежник находится с поднятым пером. | Язык и среда только названы, детали решатель восстанавливает сам. Ограничений нет. |
| 3 | Для исполнителя, который находится в начале координат с поднятым пером и понимает команды «опусти перо» и «переведи в точку (x, y)», напишите последовательность из пяти команд, по которой он изобразит треугольник, положение вершин которого на координатной плоскости определяется парами чисел (1,1), (3,5), (5,2). | Среда существования процесса и язык явно не указаны, но могут быть доопределены по остальным явно заданным компонентам задачи, есть ограничения |
Примером формулировки, в которой не указаны стартовые позиции (задачи на подбор множества исходных состояний объекта, из которых можно прийти к заданному конечному его состоянию), может быть следующая: «Разработать программу для Чертежника, в результате которой будет изображена фигура (дан чертёж фигуры на координатной плоскости, например «пятиконечная звезда», «раскрытый конверт»). Подобрать такое исходное положение чертежника, чтобы фигуру можно было нарисовать, не поднимая пера и не проходя дважды по одной и той же линии».
В качестве примера формулировки, в которой не конкретизировано конечное состояние (цель), т.е. в качестве примера задачи на усмотрение задачной ситуации и определение задачной системы (= составление задачи на моделирование процесса на основе некоторого ориентира) предлагаем такую формулировку: «Задана конкретная обстановка для Робота (КУМир) (дан рисунок поля, на котором есть лабиринт из стен, а некоторые клетки в лабиринте радиоактивны). Составьте задачу на разработку программы для Робота и решите её».
Обращение задач на моделирование процесса
Если в системе задачи на разработку модели процесса сама модель дана и требуется определить какую-либо деталь процесса ее создания, не реализуя при этом смоделированный процесс, а только изучая его описание, то группа таких формулировок-вопросов рассматривается как взаимообратные. При этом прямой задачей всегда будет являться та, в которой модель объявлена требованием, а обратные задачи будут отличаться по типу от прямой, т. е. по сути, являются качественными задачами-вопросами. Поэтому таблицу 2 можно продолжить, добавив в нее обратные качественные задачи-вопросы. При этом мы видим, что то, что было требованием (модель процесса), становится базисом или основой для данных задач. Формулировки обратных задач представлены в таблице 5.
Таблица 5 – Сопоставление взаимообратных задач на разработку модели процесса
| Прямая задача | Д  ано описание исполнителя «Черепаха». Составьте алгоритм для Черепахи таким образом, чтобы в результате его выполнения в центре арены появился ромб, представленный на рисунке. | |||||||
| Базис | Условие | Требование | ||||||
| Структу-ра задачной системы | Язык | Среда | Ограни-чения | Стартовые позиции | Цель | Модель процесса | ||
| Словесно-пошаговая запись | Исполнитель Черепаха действует на песчаной арене, имеющей форму квадрата со стороной 500 пикселей. СКИ: вперед (n), вправо (m), поднять хвост опустить хвост | квадрат со стороной 500 пикселей | Черепаха находится в центре арены, ее голова направлена к верхней стороне квадрата, хвост опущен | Изображен ромб в центре арены, представлен-ный на рисунке, Черепаха находится в центре арены, ее голова направлена к верхней стороне квадрата, хвост опущен | нач поднять хвост вперед (30) опустить хвост вправо (135) вперед (50) вправо (135) вперед (50) вправо (135) вперед (50) вправо (135) вперед (50) вправо (90) поднять хвост вперед (30) вправо (180) опустить хвост кон (далее в таблице эта последователь-ность команд обозначается как алгоритм) | |||
| Обратная задача 1 (на определение стартовых позиций процесса) | Условие | Условие | Условие | Требование | Условие | Базис | ||
| Исполнитель Черепаха действует на песчаной арене, имеющей форму квадрата со стороной 500 пикселей, и имеет такую СКИ: вперед (n), вправо (m), поднять хвост, опустить хвост. К 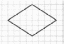 акими могут быть допустимые начальные состояния Черепахи (где может находиться на арене и куда может быть направлена ее голова), чтобы после выполнения алгоритма (заданной последовательности команд) появилась фигура в центре арены, представленная на рисунке. | ||||||||
| ОЗ 2 (на определение языка) | Требование | Условие | Условие | Условие | Условие | Базис | ||
| Укажите, в какой форме записи представлен данный алгоритм. | ||||||||
| ОЗ 3 (на определение среды) | Условие | Требование | Условие | Условие | Условие | Базис | ||
| Для какого исполнителя представлен данный алгоритм? | ||||||||