ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 349
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Изобара - это линия, соединяющая точки с одинаковыми значениями пластовых давлений, приведенных к условной уровенной поверхности
-
Одномерный установившийся поток жидкости и газа в пористой среде в радиально- сферическом случае. Схема притока к скважине, вскрывающей кровлю пласта.
Одномерным называется фильтрационный поток жидкости или газа, в котором скорость фильтрации, давление и другие характеристики течения являются функциями только одной координаты, отсчитываемой вдоль линии тока. Одномерные фильтрационные потоки обладают различной симметрией. К одномерным потокам относятся:1) прямолинейно-параллельный:2) плоско-радиальный;3) радиально-сферический.Радиально-сферический поток. Траектории всех частиц жидкости - прямолинейные горизонтальные прямые, радиально сходящиеся к центру полусферического забоя; изотахи и эквипотенциальные поверхности перпендикулярны траекториям и образуют сферические поверхности. Скорость фильтрации в любой точке потока является функцией только расстояния этой точки от центра забоя. Следовательно, этот вид фильтрационного потока также является одномерным.
Такой поток может реализовываться, когда скважина вскрывает только плоскую горизонтальную, непроницаемую кровлю пласта (рис.3.3). Пласт при этом должен быть неограниченной толщины, а забой иметь полусферическую форму. Приближение к данному виду потока тем лучше, чем глубина вскрытия меньше толщины пласта.
Описанные три вида одномерного потока играют большую роль при решении многих задач нефтегазопромысловой практики. Они лежат в основе ряда исследований закономерностей течения жидкости в пласте, в зависимости от принятой системы разработки или от конструктивных особенностей скважин. Естественно, моделируя каждый из трёх видов одномерного потока, мы прибегаем к некоторой схематизации реальных пластов и течений жидкости. Тем не менее, рассмотренные схемы не только воспроизводят, хотя и приближенно простейшие случаи течения жидкости в реальном пласте, но и помогают изучать более сложные виды потоков пластовой жидкости в тех случаях, в которых сложный фильтрационный поток удобно представить себе состоящим из простейших видов потока
-
Формула для расчета дебита газовой скважины для плоско-радиального притока идеального газа к совершенной скважине.
Для установившегося плоскорадиального потока однородной жидкости по закону Дарси дебит скважины можно определить по формуле
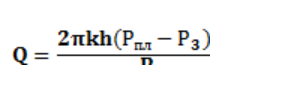
где Q — дебит скважины (объем жидкости, поступающей на забой скважины в единицу времени); k — проницаемость пласта; h — толщина пласта; Рпл — пластовое давление; Рз — забойное давление в скважине; — вязкость жидкости; RK и rс — радиусы контура питания и скважины, соответственно
-
Виды несовершенства скважин. Схемы притоков однородной жидкости к несовершенным скважинам. Приведенный радиус скважины. Коэффициент несовершенства.
Различают три вида несовершенства скважин, рис. ниже:
1) несовершенная скважина по степени вскрытия - это скважина с открытым забоем, вскрывшая пласт не на всю мощность, а только на некоторую глубину b.
2) несовершенная скважина по характеру вскрытия – это скважина, вскрывшая пласт на всю его мощность, но сообщающаяся с пластом только через отверстия в колонне труб (перфорация), в цементном кольце или в специальном фильтре.
3) на практике чаще всего встречаются скважины несовершенные как по степени, так и по характеру вскрытия пласта.
При расчете несовершенных скважин нередко используют понятие приведенного радиуса несовершенной скважины
где rC – радиус несовершенной скважины, С – коэффициент несовершенства.
Приведенный радиус - это радиус такой совершенной скважины, дебит которой равняется дебиту данной несовершенной скважины при тех же условиях эксплуатации.
Отношение дебита гидродинамически несовершенной скважины к дебиту совершенной скважины характеризует степень несовершенства скважины и называется коэффициентом несовершенства. Коэффициент несовершенства зависит: от относительного вскрытия пласта; от числа отверстий, приходящихся на 1м колонны, размеров и формы отверстий; от глубины прострела. Дебит несовершенной скважины при одинаковых прочих условиях меньше дебита совершенной скважины, поэтому коэффициент несовершенства всегда меньше единицы.
-
Задача Бакли-Леверетта. Допущения. Смысл функции Бакли-Леверетта. Ее зависимость от насыщенности.
Задачи двухфазной фильтрации без учета капиллярных сил известны как задачи (модель) Баклея - Леверетта.Для обоих случаев одномерного потока (прямолинейно-параллельного и плоскорадиального) это приводит к классической в теории вытеснения модели Баклея - Леверетта.В рассматриваемом случае важное значение имеет так называемая функция Баклея - Леверетта или функцией распределения потоков фаз f(s), которая имеет простой физический смысл. Действительно, данная функция представляет собой отношение скорости фильтрации вытесняющей фазы к суммарной скорости, и равна объемной доле потока вытесняющей жидкости (воды) в суммарном потоке двух фаз. Таким образом, функция Баклея - Лаверетта определяет полноту вытеснения и характер распределения газоконденсатонасыщенности по пласту. Задачи повышения нефте- и газоконденсатоотдачи в значительной степени сводятся к применению таких воздействий на пласт, которые в конечном счете изменяют вид функции f(s) в направлении увеличения полноты вытеснения. Характерной особенностью графика f(s) является наличие точки перегиба sп , участков вогнутости и выпуклости, где вторая производная f//(s) соответственно больше и меньше нуля. Эта особенность в большой степени определяет специфику фильтрационных задач вытеснения в рамках модели Баклея - Леверетта.Физической особенностью модели двухфазного вытеснения Баклея – Леверетта является зависимость скорости распространения того или иного значения насыщенности от величины этой насыщенности. Это явление называется дисперсией волн. В общем случае неодномерного вытеснения, а также при учете сжимаемости одной из фаз рассмотренная задача уже не сводится к одному уравнению для насыщенности. Необходимо совместно определять давление и насыщенность. Численные решения таких задач могут быть получены лишь на ЭВМ.
-
Задача Бакли-Леверетта. Распределение насыщенности в пласте в различные моменты времени.
В случае одномерного течения несжимаемых несмешивающихся жидкостей в условиях, когда можно пренебречь капиллярным давлением, а также влиянием силы тяжести, процесс вытеснения допускает простое математическое описание.Для обоих случаев одномерного потока (прямолинейно–параллельного и плоскорадиального) это приводит к классической в теории вытеснения модели Баклея—Леверетта.Рассмотрим пласт толщиной h и длиной L Слева, за границей нефтяного пласта, находится законтурная вода. Из пласта происходит отбор нефти с постоянным расходом Q
o. Вода и нефть считается несжимаемыми. В законтурной области водонасыщенность равна единице, а в нефтяном пласте водонасыщенность равна остаточной водонасыщенностиσво. Необходимо рассчитать распределение водонасыщенности с различные моменты времени.
Эта задача описывается уравнениями неразрывности:
| |
И обобщенным законом Дарси:
| |
Сложим уравнения неразрывности. Сумма насыщенностей равна единице, поэтому:
| |
Функция Баклея—Леверетта определяет полноту вытеснения и характер распределения насыщенности по пласту.