Файл: 1. 1 Классификация, особенности, порядок проведения и приборы, используемые для съемки местности 4.docx

Таблица 1 – зависимости между дирекционными углами и румбами

Вычисление приращений координат производится по формулам прямой геодезической задачи (14), (15):

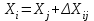, (14)

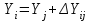, (15)

где 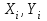- определяемые координаты i-ой точки теодолитного хода;

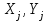- известные координаты j-ой точки теодолитного хода;

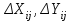- приращения координат i-ой точки относительно j-ой, вычисляемые по формулам (16), (17):

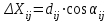, (16)

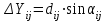, (17)

где 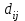- горизонтальное проложениеi-j стороны теодолитного хода;

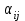- дирекционный угол i-jстороны теодолитного хода.

Уравнивание приращений координат и оценка точности линейных измерений включает в себя:

• 
  вычисление невязок линейных измерений в проекции на ось Х - ;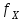
  
• 
  вычисление невязок линейных измерений в проекции на ось У - ;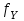
  
• 
  вычисление абсолютной невязки измерений;
  
• 
  вычисление относительной невязки и оценка точности линейных измерений;
  
• 
  вычисление и внесение поправок в приращения координат;
  
• 
  контроль вычислений [8,10].
  

Вычисление невязок производят по следующим формулам для замкнутого хода (18), (19):

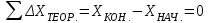, (18)

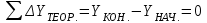. (19)

---

Вычисление абсолютной невязки 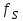производится по формуле (20):

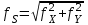. (20)

В зависимости от абсолютной ошибки вычисляют относительную ошибку 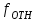по формуле (21):

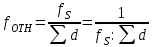, (21)

где 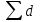- сумма горизонтальных проложений сторон теодолитного хода или периметр полигона.

После оценки точности линейных измерений необходимо вычислить поправки в приращения координат. Поскольку линейные измерения являются неравноточными, и зависят от измеренного расстояния, невязки распределяются пропорционально горизонтальным проложениям сторон теодолитного хода по формулам (22):

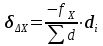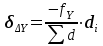, , (22)

где 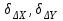- поправки, вносимые в соответствующие приращения координат;

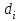- горизонтальное проложение стороны теодолитного хода, в которую вносятся поправки.

Для контроля вычислений необходимо вычислить сумму всех вносимых поправок, которая должна бать равна невязке, взятой с обратным знаком, а именно (23):

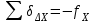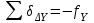, . (23)

Вычисление исправленных приращений координат производится по формулам (24), (25):

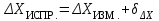, (24)

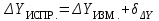. (25)

Далее по исправленным значениям приращений координат по формулам прямой геодезической задачи последовательно, начиная с начального исходного пункта, вычисляют координаты пунктов теодолитного хода (26)[8,10]:

, . (26)

---

Получившееся координаты вершин хода приведены ниже в «Ведомость вычисления координат точек теодолитного хода»

Вариант №3 – Злобина О.С.

Ведомость вычисления координат точек теодолитного хода

№ вершин хода	Измеренные углы	Исправлен ные углы	Дирекционные углы, 	Румбы, r	Горизонтальные проложения, d	Приращения координат, м						Координаты точек, м			№ вершин хода
						вычисленные			исправленные
						X	Y	X		Y	Х		У
1	2	3	4	5	6	7	8	9		10	11		12	13
1	88º14ʹ		217º03ʹ		26,73	-24,55	-10,58	-24,58		-10,56	+120,00		-20,00	1
2	184º02ʹ	184º02ʹ24ʹʹ									95.42		-30.56	2
			221º 5ʹ24``	ЮЗ: 33º02ʹ36ʹʹ	58,35	-55,08	-19,26	-55,10		-19,25
3	91º55ʹ	91º55ʹ24ʹʹ									40.32		-49.81	3
			309º 10ʹ0``	ЮЗ: 129º10ʹ0ʹʹ	70,50	+21,03	-67,29	21,00		-67,28
4	90º37ʹ	90º37ʹ24ʹʹ									61.32		-117.09	4
			38º32ʹ36ʹʹ	СЗ: 218º33ʹ12ʹʹ	90,60	+86,77	+26,08	86,75		26,09
5	85º10ʹ	85º10ʹ24ʹʹ									148.07		-91	5
			133º22ʹ12ʹʹ	СВ: 46º37ʹ48ʹʹ	76,33	-28,05	+70,99	-28,07		71,00
1	88º14ʹ	88º14ʹ24ʹʹ									120		-20	1
			225º7ʹ48ʹʹ	ЮВ: 45º7ʹ48ʹʹ
βизм. =539058`
βтеор. = 180*(n -2)=540000`					Р=322.51	fx =+0.12	fy =-0.06	fx =		fy =00

---

f_βизм. = β_изм/ - β_теор. =-00º02ʹ

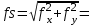
f_βдоп. = ± 1,5ʹ√n =

f_βдоп.= ± 1,5ʹ√n =± 1,5ʹ√5 =3.20

---

3.2 Определение площади полигона аналитическим способом

Основным способом вычисления площадей земельного участка, когда его граничные точки закреплены и для них известны координаты, является аналитический [8]. В этом случае площади земельных участков (полигонов) вычисляют по формулам (27), (28):
(27)

………………………………………(28)
где

x_i ,y_i – координаты точек;

n-вершина хода;

(n+1) – номер последующей вершины;

(n+1) – номер предыдущей вершины;
Обычно по одной из приведенных формул вычисляют площадь участка, а по другой – выполняют контрольное определение. Площади, выходящие за пределы полигона, но входящие в данный земельный участок, определяют, как сумму площадей треугольников, прямоугольников и трапеций, длины которых получены из измерений на местности. Иногда элементы простейших геометрических фигур определяют по плану. Значение площадей получают по известным формулам тригонометрии[8].

Полученный результат определения площади полигона аналитическим способом приведен в «Ведомость вычисления площади участка по координатам»
Ведомость вычисления площади участка по координатам

№ № вершин	Координаты точек		Разности (Δ)				Произведения
	Хi	Yi	Yi+1-Yi-1		Xi-1-Xi+1		Xi(Yi+1-Yi-1)		Yi(Xi-1-Xi+1)
1	120	-20	6,72		22,56		805,87		-451,29
2	95,42	-30,56	-4,78		29,77		-456,17		-909,68
3	40,32	-49,81	-20,54		6,86		-828,28		-341,87
4	61,32	-117,09	-17,41		-29,85		-1067,32		3495,57
5	148,07	-91	35,20		-28,20		5212,06		2566,55
Контроль:				0		0		3666,16		4359,28
								S=7990920,65м2

---