МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение

высшего образования

«Тольяттинский государственный университет»
Институт математики, физики и информационных технологий

(наименование института полностью)
Кафедра ______Высшая математика и математическое образование ____________

(наименование кафедры/департамента/центра полностью)

44.04.01 Педагогическое образование

(код и наименование направления подготовки, специальности)

Математическое образование

(направленность (профиль) / специализация)


КОЕТРОЛЬНАЯ РАБОТА
по учебному курсу «Теория и методика обучения математике в профильной школе 2»

Студент	Курганова И.В.
	(И.О. Фамилия)
Группа	Ммд-2101а
Преподаватель	Р.А. Утеева
	(И.О. Фамилия)

Тольятти 2022


Вариант № 1
1. Найти все целые значения х, удовлетворяющие неравенству .



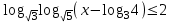2. Дифференцируема ли функция: 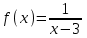в точке х = 3? Если нет, то почему? В каких точках эта функция дифференцируема? Ответ сопроводить графиком.

Предложенная функция не определена в точке x=3, производная в точке x=3 не существует. Данная функция дифференцируема во всех точках, кроме х=3. В любой точке кроме x=3 можно провести касательную.

---

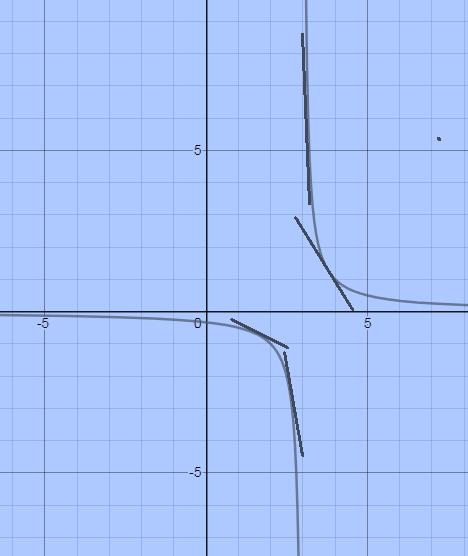
3. Провести касательную к графику функции 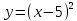в точке (2;2).

Через точку (2;2) график не проходит.

_4. Решая неравенство 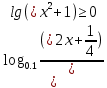_{на основе понятия «дробь неотрицательна, если…» ученик получил в ответе, что данное неравенство не имеет решения. Указать на ошибки в решении ученика (если таковые имелись). Привести верное решение по этому способу.}

ОДЗ:

{2x+(1/4)>0 ⇒ x > –1/8

{lg(x2+1) ≠ 0 ⇒ x2+1 ≠ 1 ⇒ x2 ≠ 0 ⇒ x ≠ 0

x ∈ (–1/8;0) U(0;+ ∞ )

Дробь неотрицательна...если числитель и знаменатель имеют одинаковые знаки ( с учетом второго неравенства ОДЗ, знаменатель не должен равняться 0) это приводит нас в двум системам неравенств:

1)

{log0,1(2x+(1/4))≥0 ⇒ log0,1(2x+(1/4)) ≥ log0,11⇒ (2x+(1/4)) ≤ 1

{lg(x2+1) >0 ⇒ lg(x2+1) > lg1 ⇒ x2+1> 1 ⇒ x2>0 ⇒ x ≠ 0

или

2)

{log0,1(2x+(1/4)) ≤ 0 ⇒ log0,1(2x+(1/4)) ≤ log0,11⇒ 2x+(1/4) ≥ 1

{lg(x2+1) <0 ⇒ lg(x2+1) < lg1 ⇒ x2+1< 1 ⇒ x2<0 – неравенство неверно при каких x, значит и вся система не имеет решений

Из 1)

{2x ≤ 1–(1/4) ⇒ x < ≤ 3/8

{x ≠ 0

С учетом ОДЗ получаем ответ

(–1/8;0) U (0;3/8]

2.

Область определения

x+9 >0 ⇒ x> – 9

Находим производную:

y`=2x+9−2

y`=0

2x+9−2=0

2−2⋅(x+9)x+9=0

2−2x−18x+9=0

−2x−16x+9=0

–2x–16=0

x=–8

Исследуем точку х=–8 на экстремум.

Проверяем знак производной при переходе через эту точку.

При x=–8,5

y`=(2/0,5)–2 >0, ставим + на интервале, содержащем точку (х=–8,5)т.е. на (–9;–8 )

(–9) _+_ (–8) ___–___

x=–8 – точка максимума, производная меняет знак с + на –

y(–8)=2ln1–2·(–8)+13=16+13=29 – наибольшее значение функции.

y``=−2(x+9)2<0 на ОДЗ

Кривая выпукла вверх


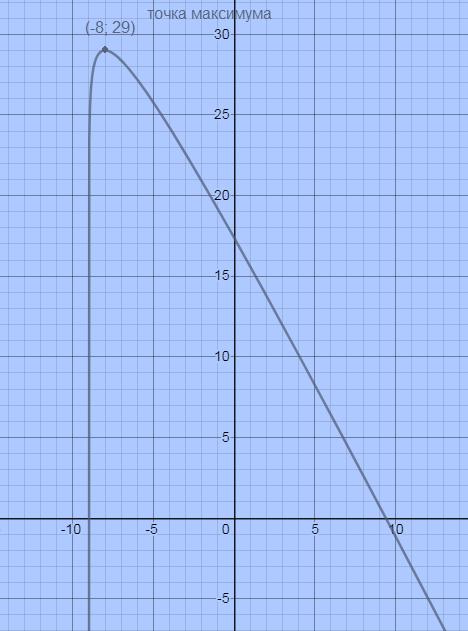
5. Исследовать функцию и построить ее график

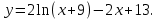
Область определения:

x+9 >0

x>–9

y`=2/(x+9) – 2

y`=0

2/(x+9) – 2=0

2/(x+9) = 2

1/(x+9)=1

x+9=1

x=–8

x=–8– точка максимума, так как при переходе через точку производная меняет знак с + на –

y`(–8,5) >0

y`(7,5) <0

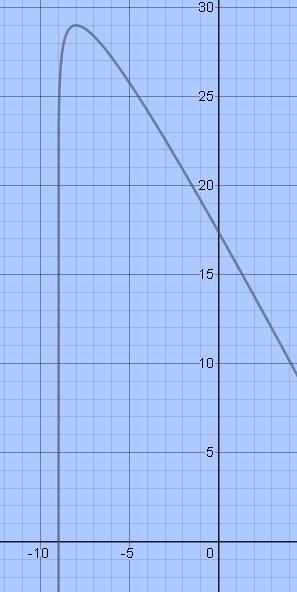
Вертикальная асимптота x=–9

limx→−9(2ln(x+9)−2x+13)=−∞

Горизонтальной асимптоты нет:

---

limx→+∞(2ln(x+9)−2x+13)=∞

Проверяем наличие наклонной асимптоты:

k=limx→+∞f(x)x=limx→+∞2ln(x+9)−2x+13x=limx→+∞(2ln(x+9)−2x+13)‘(x)‘=limx→+∞2x+9−21=−2

b=limx→+∞(f(x)−kx)=limx→+∞(2ln(x+9)−2x+13+2x)=∞

Нет наклонной асимптоты



6.При выполнении задания вычислить интеграл 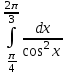, учащийся получил в ответе положительное число. Прав ли он? Если нет, то в чем заключается ошибка? Дать верное решение.

Функция y=1/cos2x не является непрерывной на отрезке [π/4; 2π/3]

Это несобственный интеграл второго рода:

∫π2π41cos2xdx+∫2π3π21cos2xdx=(tgx)|π2π4+(tgx)2π3π2

Интеграл расходится, так как tgx при x → (π/2) –0 равен + ∞

при x → (π/2) +0 равен – ∞



7. Верно ли, что если функция непрерывна в точке, то она имеет в этой точке производную? Ответ поясните на примерах.

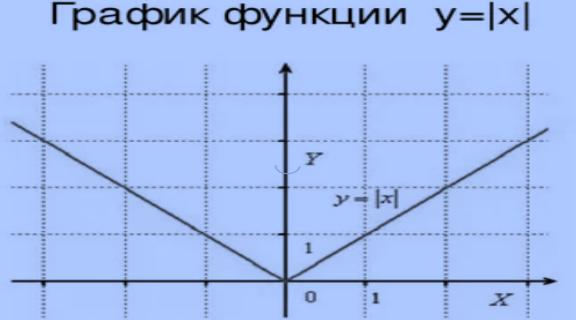
Нет.

Например, функция y=|x| непрерывна 0, но производная не существует.

Если х ≥ 0 , то |x|=x

x`=1

Если х < 0, то |x|=–x

(–х)` = – 1

или так:


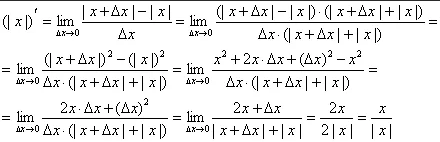
0>0>0>

---

Смотрите также файлы

• Разведывательный анализ данных.docx

• Модернизация системы инженернотехнической защиты.docx

• Определение уранового эквивалента суммарного содержания естественнорадиоактивных элементов по данным интегрального гаммаметода.docx

• Методическая разработка для проведения практического занятия по пожарностроевой подготовке с личным составом 39 пч фпс тема занятия Боевое развёртывание с установкой переносного лафетного ствола время.doc

• Утверждаю начальник 27 псч 2 псо фпс гпс гу мчс россии по Калужской области.docx