_{Министерство науки и высшего образования Российской Федерации}

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Псковский государственный университет»
Передовая инженерная школа гибридных технологий в станкостроении

Союзного государства

Отчет по лабораторной работе №1

по дисциплине: «Метрологическое обеспечение электрических измерений ЗФО»

на тему «Исследование методов измерения больших и малых сопротивлений (метод амперметра и вольтметра)»

Вариант 3

	Выполнил 1433-07 Гвоздс С. Степанов А.С.
	Проверил к.т.н., доцент Бандурин И.И.

Псков

2023

Цель работы:

1. 
   Изучение методов и средств измерения сопротивлений.
   
2. 
   Ознакомление с методикой измерения сопротивлений приборами непосредственной оценки.
   

Основные теоретические положения
Измерение сопротивлений представляет собой наиболее обширную область электроизмери­тельной техники, как в отношении методов измерения, так и используемой аппаратуры.

Разнообразие методов в значительной степени объясняется весьма широким диапазоном вели­чин сопротивлений, которые подлежат измерению (от10^-6до10⁺¹⁶) Ом, большим разнообразием объектов измерения, точностью, предъявляемой к измерениям.

Метод амперметра и вольтметра является наиболее легко осуществимым, а потому довольно распространенным.

В зависимости от соотношения сопротивлений измерительного прибора и измеряемого объекта 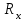применяют так называемые схемы правильного включения амперметра (рис. 1.1) или вольтметра (рис.1.2)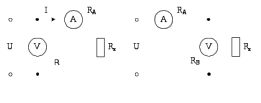

---

Рис. 1.1. Схема правильного включения амперметра

Рис. 1.2. Схема правильного включения вольтметра

В схеме на рисунке 1.1 амперметр подключается последовательно с измеряемым сопротивлением. Вольтметр при этом подключается параллельно амперметру и резистору R_x. Из неизвестных величин (U_x,I_x) только I_x измеряется, верно. Входное напряжение U = U_x+ U_A превышает истинное значение U_x на U_A= I_x· R_A. Это - методическая погрешность, которая снижается при R_A 0.

Вариант схемы (рис.1.2) отличается тем, что вольтметр подключается параллельно резисторуR_x. Из неизвестных величин (U_x,I_x) правильно измеряется только напряжение U_x. Общий ток при этом I= I_x· I_V превышает истинное значение на величину тока, текущего через вольтметр I_V= U_x/R_V. Методическая погрешность в этом случае тем меньше, чем больше R_V.

Величина сопротивления, вычисленная по показаниям приборов, отличается от его действительного значения. Эта погрешность может быть учтена, если известны сопротивления приборов. Сопротивление, подсчитанное по показаниям приборов.

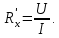(1.1)

Относительная погрешность измерения для схемы (рис. 1.1)

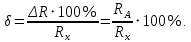(1.2)

Из последнего выражения видно, что эта схема более пригодна для измерения больших сопротивлений по сравнению с сопротивлением амперметра.

Для схемы (рис. 1.2) справедливы равенства

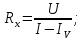	(1.3)
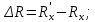	(1.4)
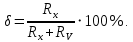	(1.5)

---

Выражение для относительной погрешности 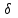показывает, что эту схему целесообразно применять для измерения сопротивлений, малых по сравнению с сопротивлением вольтметра.

Точность метода амперметра и вольтметра сравнительно невелика, но он достаточно часто используется для оценки величины измеряемого сопротивления.

Описание лабораторной установки
В данной лабораторной работе измерение сопротивлений осуществляется методами непосредственной оценки. С этой целью на виртуальном лабораторном стенде (рис.1.3) смоделированы управляемый выпрямитель, измерительные прибора магнитоэлектрической системы и органы управления



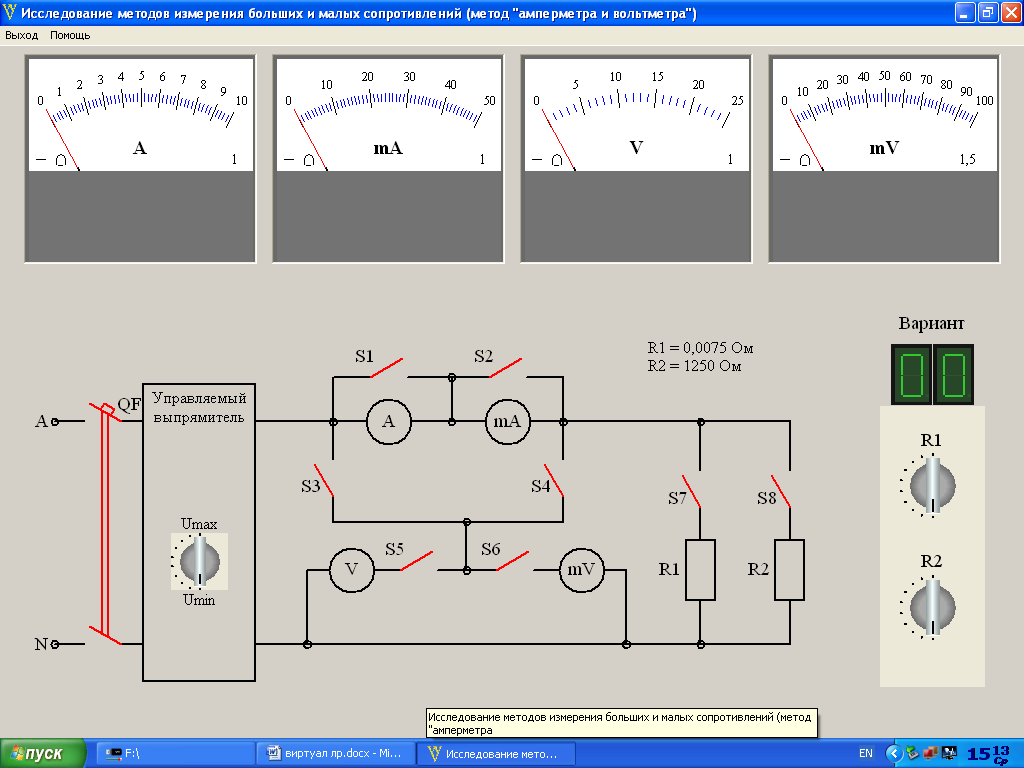
Рис.1.3. Общий вид виртуального лабораторного стенда

Подготовка к работе

1. 
   Для схем рис.1.1 и рис.1.2 записать выражения для определения величины сопротивления по показаниям амперметра и вольтметра, и мощности, рассеиваемой сопротивлением при известном номинальном токеI_ни номинальном напряжении U_н.
   

1.1 В схеме, изображенный на рис.1.1, показания вольтметра U_v равны сумме напряжений на сопротивлении R_x и на амперметре U_a. В этом случае

измеряемое сопротивление определяется по формуле: (1.6)

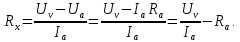	(1.6)

1.2 В схеме, изображенный на рис.1.2, показание амперметра I_a равно сумме токов в сопротивлении R_x и вольтметре I_v, следовательно, измеряемое сопротивление определяется по формуле (1.7):

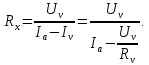	(1.7)

1.3 В схеме, изображенный на рис.1.1, показания амперметра I_a равно току проходящему через резистор I_x. По формуле (1.6) определяем сопротивление R_x, следовательно, мощность рассеивания резистора определяем по формуле (1.8):

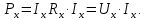(1.8)

---

1.4 В схеме, изображенный на рис.1.2, показания вольтметра U_v равно напряжению, проходящему через резистор U_x, потому что они параллельны. По формуле (1.7) определяем сопротивление R_x, следовательно, мощность рассеивания резистора определяем по формуле (1.9):

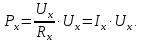(1.9)

2. 
   Вывести выражения для определения относительных погрешностей измерения сопротивлений для схем рис.1.1 и 1.2, если известны значения сопротивлений вольтметра R_v, амперметра R_a и действительные значения сопротивлений R_x.
   

2.1 Для схемы, изображенный на рис.1.1 измеренное сопротивление будет равно сумме сопротивлений R_a и R_x, так как они последовательны. Следовательно, для определения абсолютной погрешности используем формулу (2.0):

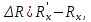(2.0)

где 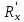- измеренное сопротивление, 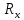– истинное сопротивление.
2.2 Формула относительной погрешности определяется по формуле (2.1):

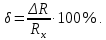(2.1)

2.3 Для схемы, изображенный на рис.1.2 измеренное сопротивление будет равно значению, которая эквивалентна сопротивлениям R_v и R_x, так как они параллельны. Следовательно, для определения абсолютной погрешности используем формулу (2.2):

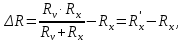(2.2)

где 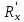- измеренное сопротивление, 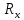– истинное сопротивление.
2.4 Формула относительной погрешности определяется по формуле (2.1).

---

2. 
   Рассчитать относительные погрешности измерения сопротивлений R_x для заданных в таблице 1 вариантов.
   

Таблица 1

Заданный параметр	Ед.измерения	Номер варианта
		3
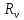	кОм	600
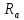	Ом	0,002
(рис.1.1)	кОм	4
(рис.1.2)	Ом	0,4

3.1 Для определения погрешности R_x(рис.1.1) справедливы формулы (2.0) и (2.1):

;


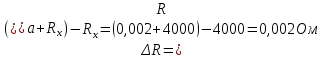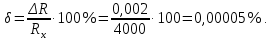
3.2 Для определения погрешности R_x(рис.1.2) справедливы формулы (2.1) и (2.2):



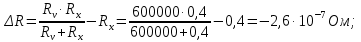
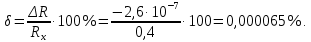
Рабочее задание

1. 
   Внимательно изучить общий вид виртуального лабораторного стенда.
   
2. 
   С помощью интерактивных коммутационных элементов смоделировать схему для измерения большого сопротивления (см. рис.1.1). В схеме использовать приборы: вольтметр с пределом измерения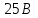 и миллиамперметр с пределом измерения 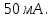Произвести измерения при пяти значениях напряжения. Результаты измерений занести в таблицу 2.
   
3. 
   С помощью интерактивных коммутационных элементов смоделировать ошибочную схему для измерения большого сопротивления (см. рис.1.2). В схеме использовать те же приборы, что и в предыдущем пункте. Произвести измерения при пяти значениях напряжения. Результаты измерений занести в таблицу 1.2.
   
4. 
   С помощью интерактивных коммутационных элементов смоделировать схему для измерения малого сопротивления (см. рис.1.2). В схеме использовать амперметр с пределом измерения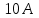 и милливольтметр с пределом измерения 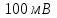. Измерения произвести при пяти значениях напряжения. Результаты измерений занести в таблицу 1.2.
   
5. 
   С помощью интерактивных коммутационных элементов смоделировать ошибочную схему для измерения малого сопротивления (см. рис.1.1). В схеме использовать те же приборы, что и в предыдущем пункте. Произвести измерения при пяти значениях напряжения. Результаты измерений занести в таблицу 1.2.
   

---

Смотрите также файлы

• Год 2009 Автор научной работы.docx

• Лабораторная работа по дисциплине Метрология, стандартизация и сертификация.docx

• Количественная теория денег и ее эволюция в монетарных концепциях 080109. 07. 190. 00 Пз.rtf

• Литература xx века Учеб для вуз. 2е изд., испр и доп. М. Высш., 2004. 559 с.docx

• абылдаан рбанбеков. Ш орындаан Алимбекова. М тркістан 2023 ж.docx