ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 146
Скачиваний: 11
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ОСНОВЫ И ПРАВИЛА СТРЕЛЬБЫ
1. Единица измерения углов «тысячная». Соотношение между градусом и «тысячной», запись и произношение «тысячной». Формула «тысячной», ее вывод и применение (привести пример.
За единицу измерения углов (меру углов) в артиллерийско-стрелковой практике принимают центральный угол, опирающийся на дугу, длина которой равна 1/6000 части длины окружности. Эту угловую единицу называют делением угломера.
Между делением угломера и градусным измерением существует следующая зависимость:
360° = 6000 делений угломера (записывается 60-00);
180°= 3000 делений угломера (записывается 30-00);
90°= 1500 делений угломера (записывается 15-00);
9°= 150 делений угломера (записывается 1-50);
6° = 100 делений угломера (записывается 1-00) и т. д.
Зная эту зависимость, можно переводить деления угломера в градусы и минуты и обратно.
Пример. Поле зрения прицела УСП-1 (1П29 «Тюльпан») равняется 8°. Сколько это составляет делений угломера?
Решение
6° = 100 д.у.;
8° = (100/6) × 8
Так как одному делению угломера соответствует дуга равная одной шеститысячной длины окружности, то, зная длину окружности, получаем:
При большинстве практических расчетов округленно принимают, что длина дуги угла в одно деление угломера равна 1/1000 длины радиуса окружности. Поэтому деление угломера называют тысячной. Относительная ошибка, которая допускается при таком округлении, равна 5%, т.е. тысячная на 5% меньше деления угломера. В практике при большинстве расчетов этой ошибкой пренебрегают.
Деление угломера (тысячная) позволяет просто решать целый ряд задач. Если представить, что глаз наблюдателя является центром окружности дуга, которой проходит через ориентир (предмет, цель), то радиус этой окружности будет являться дальностью наблюдения, поэтому длина дуги, соответствующая одному делению угломера, будет равна одной тысячной дальности наблюдения.
Углу в одну тысячную соответствует дуга, равная:
на расстоянии 2000 м – 2 м;
на расстоянии 1600 м– 1,6 м и т.д.
Углу в несколько тысячных соответствует длина дуги L, равная одной тысячной дальности умноженной на угол, содержащий У тысячных, учитывая, что дуга L приблизительно равна величине В (рис.1), получаем:
где, Д – дальность до наблюдаемого объекта в метрах, В – линейная величина объекта (высота, длина, ширина) в метрах, У – угловая величина объекта в тысячных.
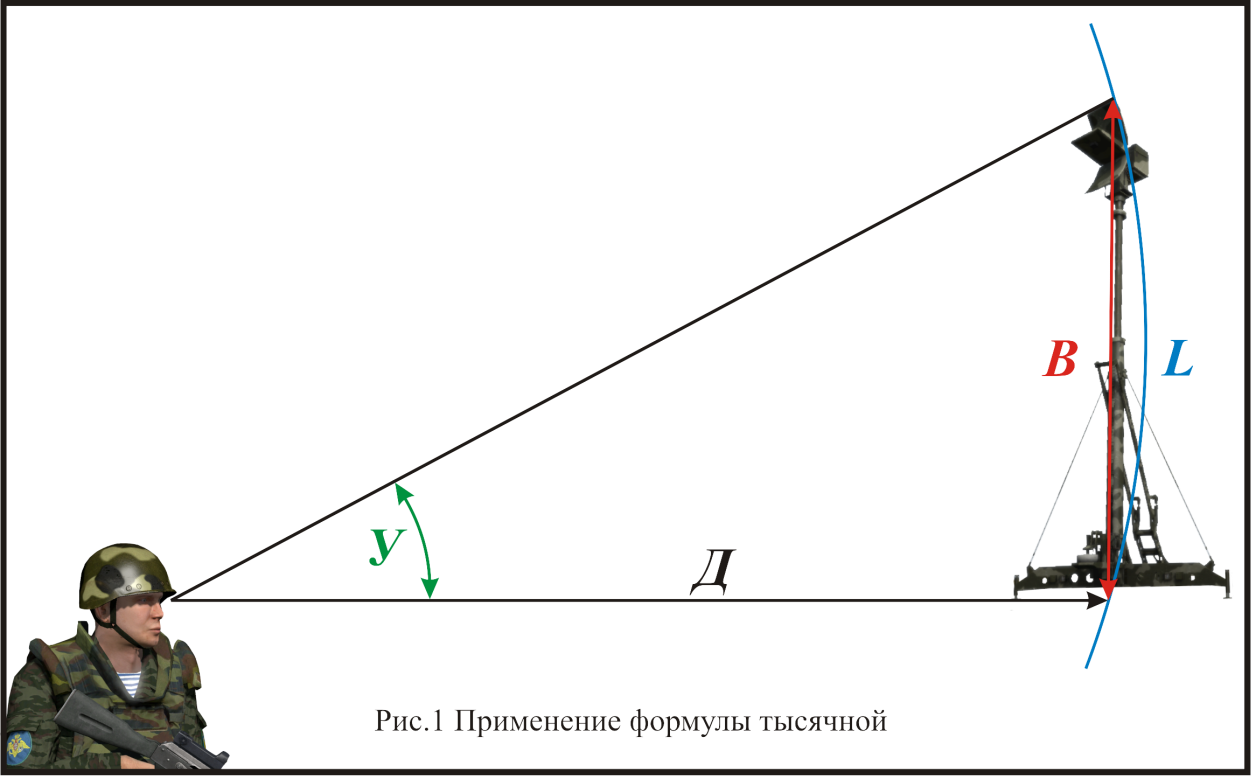
Приведенные формулы называют формулами тысячной
Пример. Танк противника длиной 6 м, рассматриваемый в бинокль Б8х30, занял одно малое деление угломерной шкалы. Определить дальность до танка.
Решение. Цена малого деления угломерной шкалы бинокля равна 0-05.
Д = (6∙1000)/5 = 1200 м.
Для измерения углов простейшим способом можно использовать зависимость, что 1 мм любого подручного предмета удаленного от глаза на 50 сантиметров покрывает угловую величину равную 0-02.
2. Рассеивание снарядов при стрельбе. Закон рассеивания. Его характеристика.
Рассеиванием снарядов или траекторий называется явление разбрасывания снарядов при стрельбе из одного и того же оружия в одинаковых условиях. Большинство причин, обусловливающих рассеивание пуль (гранат) подчиняется нормальному закону ошибок, который в отношении к рассеиванию пуль (гранат) называется законом рассеивания.
Кратко закон рассеивания формулируется следующим образом:
При достаточно большом числе выстрелов, произведенных практически в одинаковых условиях, рассеивание снарядов:
-
неравномерно относительно центра рассеивания снарядов; -
симметрично относительно осей рассеивания; -
не беспредельно относительно площади рассеивания.
Закон рассеивания характеризует три основные положения:
-
Точки встречи (пробоины) на площади рассеивания располагаются неравномерно – гуще к центру рассеивания и реже к краям площади рассеивания. -
На площади рассеивания можно определить точку, являющуюся центром рассеивания (средней точкой попадания), относительно которой распределение точек встречи (пробоин) симметрично. -
Точки встречи (пробоины) в каждом частном случае занимают не беспредельную, а ограниченную площадь.
3. Способы определения средней точки попадания.
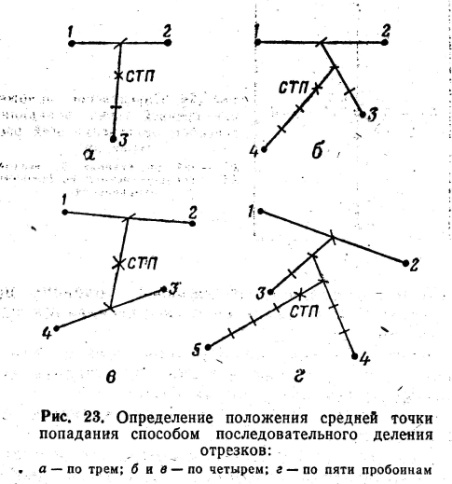
№1 - Способ последовательного деления отрезков.
№2 - Способом проведения осей рассеивания.
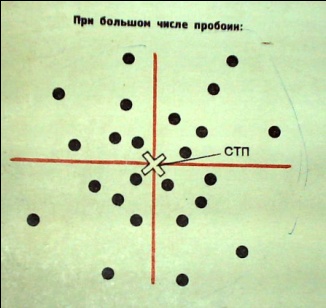
Для этого нужно:
-
Отсчитать нижнюю (ближнюю) половину пробоин и определить ее осью рассеивания по высоте; -
Отсчитать таким же порядком правую или левую половину пробоин и отделить ее осью рассеивания по боковому направлению; -
Пересечение осей рассеивания является средней точкой попадания.
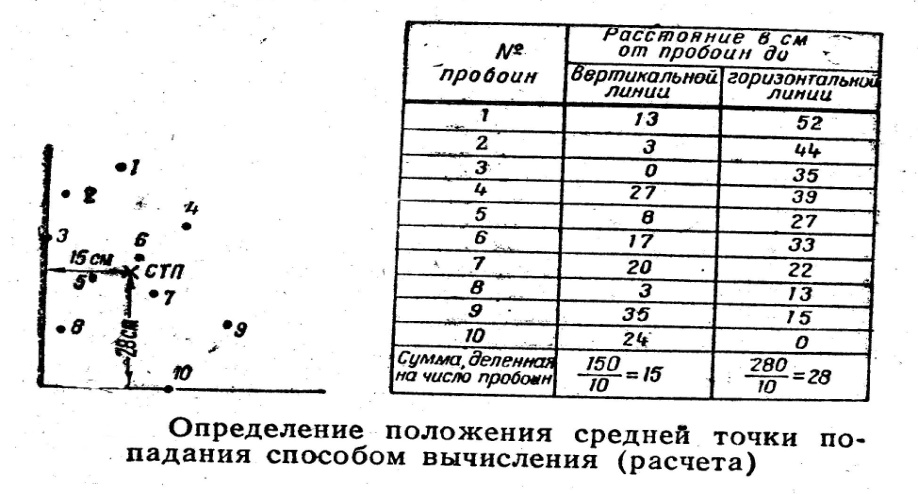
№3 - Способом вычисления (расчета).
Для этого необходимо:
-
Провести через левую (правую) пробоину вертикальную линию, измерить кратчайшее расстояние от каждой пробоины до этой линии, сложить все расстояние от вертикальной линии и разделить сумму на число пробоин; -
Провести через нижнюю (верхнюю) пробоину горизонтальную линию, измерить кратчайшее расстояние от каждой пробоины до этой линии, сложить все расстояние от горизонтальной линии и разделить сумму на число пробоин. Полученные числа определяют удаление средней точки попадания от указанных линий.
-
Траектория полета снаряда (пули) в воздухе и ее элементы. Формы траектории и их практическое значение.
Траекторией называется кривая линия, описываемая центром тяжести пули (гранаты) в полете.
Пуля (граната) при полете в воздухе подвергается действию двух сил: силы тяжести и силы сопротивления воздуха. Сила тяжести заставляет пулю (гранату) постепенно понижаться, а сила сопротивления воздуха непрерывно замедляет движение пули (гранаты) и стремится опрокинуть ее. В результате действия этих сил скорость полета пули (гранаты) постепенно уменьшается, а ее траектория представляет собой по форме неравномерно изогнутую
кривую линию.
Форма траектории зависит от величины угла возвышения. С увеличением угла возвышения высота траектории и полная горизонтальная дальность полета снаряда (пули, гранаты) увеличивается, но это происходит до известного предела.
За этим пределом высота траектории продолжает увеличиваться, а полная горизонтальная дальность начинает уменьшаться.
Угол возвышения, при котором полная горизонтальная дальность полета пули (гранат и снаряда) становится наибольшей, называется углом наибольшей дальности.
Величина угла наибольшей дальности для пуль различных видов оружия составляет около 35о.
Угол бросания, отвечающий наибольшей дальности зависит от начальной скорости, массы и формы снаряда, а также от способы стабилизации снарядов в полете и может находиться в пределах от 28о до 55о.
Траектории, получаемые при углах возвышения, меньших угла наибольшей дальности, называется настильными.
Траектория, получаемая при углах возвышения, больших угла наибольшей дальности называется навесными.
При стрельбе из одного и того же оружия (при одинаковых начальных скоростях) можно получить 2 траектории с одинаковой горизонтальной дальностью: настильную и навесную. Траектории, имеющие одинаковую горизонтальную дальность при разных углах возвышения, называются сопряженными.
Навесные траектории более выгодны для поражения горизонтальных целей (окопы, покрытия блиндажей и т.д.) при стрельбе в городе через здание, при стрельбе через укрытие. Такая стрельба характерна для минометов, применяется также при стрельбе из АГС-17, ГП-25.
При стрельбе из стрелкового оружия, гранатометов, танков, БМП, БМД, используются настильные траектории. Чем настильнее траектория, тем на большем протяжении местности цель может быть поражена с одной установкой прицела (тем меньше влияние на результаты стрельбы оказывают ошибки в определении установки прицела). В этом заключается практическое значение настильной траектории.
Траектория пули в воздухе имеет следующие свойства:
- нисходящая ветвь короче и круче восходящей;
- угол падения больше угла бросания;
- окончательная скорость пули меньше начальной;
- наименьшая скорость полета пули при стрельбе под большими углами бросания - на нисходящей ветви траектории, а при стрельбе под
небольшими углами бросания - в точке падения;
- время движения пули по восходящей ветви траектории меньше, чем по нисходящей;
- траектория вращающейся пули вследствие понижения пули под действием силы тяжести и деривации представляет собой линию двоякой кривизны.
6. Прямой выстрел. Понятие дальности прямого выстрела и ее практическое значение (привести пример).
Прямым выстрелом называется выстрел, при котором траектория снаряда (пули, гранаты) на всем своем протяжении до цели не поднимается выше цели и не опускается ниже ее основания.
В пределах дальности прямого выстрела в напряженные моменты боя стрельба может вестись без перестановки прицела, при этом точка прицеливания по высоте, как правило, выбирается на нижнем краю цели.
Дальность прямого выстрела – это дальность стрельбы, при которой траектория снаряда (пули, гранаты) не поднимается выше цели.
Дальность прямого выстрела зависит от высоты цели и настильности траектория, тем больше дальность прямого выстрела и тем на большем протяжении местности цель может быть поражена с одной установкой прицела.
Дальность прямого выстрела можно определить по таблицам стрельбы путем сравнения высоты цели с величинами наибольшего превышения траектории над линией прицеливания или с высотой траектории.
Расстояние на местности, на протяжении которого нисходящая ветвь траектории не превышает высоты цели, называется поражаемым пространством (глубиной поражаемого пространства).
Глубина поражаемого пространства зависит от высоты цели),а будет тем больше, чем выше цель), от настильности траектории (она будет тем больше, чем настильнее траектория) от угла наклона местности (на переднем скате она уменьшается, на обратном скате увеличивается), превышения стреляющего над целью (чем выше стреляющий, чем меньше поражаемое пространство).
Значение поражаемого пространства заключается в том, что траектория проходит через цель и цель может быть поражена прямым попаданием при одной установке прицела и при одном и том же положении точки прицеливания по высоте. Знание глубины поражаемого пространства позволяет установить: при каком изменении расстояния до цели за счет движения стреляющего или цели можно поразить цель прямым попаданием, если дальность стрельбы и форма траектории не изменяются. В целом поражаемое пространство показывает, в какой степени оно может компенсировать ошибки стрельбы и каковы возможности получения прямого попадания в цель при данных условиях стрельбы.