Представим расчет каждого элемента в виде таблицы:

B	x1	x2	x3	x4	x5
285-(425 • 1/4):41/4	1/4-(41/4 • 1/4):41/4	1-(0 • 1/4):41/4	1/4-(-13/4 • 1/4):41/4	0-(1 • 1/4):41/4	0-(0 • 1/4):41/4
425 : 41/4	41/4 : 41/4	0 : 41/4	-13/4 : 41/4	1 : 41/4	0 : 41/4
510-(425 • 4):41/4	4-(41/4 • 4):41/4	0-(0 • 4):41/4	-1-(-13/4 • 4):41/4	0-(1 • 4):41/4	1-(0 • 4):41/4
5985-(425 • -63/4):41/4	-63/4-(41/4 • -63/4):41/4	0-(0 • -63/4):41/4	51/4-(-13/4 • -63/4):41/4	0-(1 • -63/4):41/4	0-(0 • -63/4):41/4

Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5
x2	260	0	1	6/17	-1/17	0
x1	100	1	0	-7/17	4/17	0
x5	110	0	0	11/17	-16/17	1
F(X2)	6660	0	0	42/17	27/17	0

---

---

1. Проверка критерия оптимальности.
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.

Окончательный вариант симплекс-таблицы:

Базис	B	x1	x2	x3	x4	x5
x2	260	0	1	6/17	-1/17	0
x1	100	1	0	-7/17	4/17	0
x5	110	0	0	11/17	-16/17	1
F(X3)	6660	0	0	42/17	27/17	0

Оптимальный план можно записать так:
x₁ = 100, x₂ = 260

F(X) = 12*100 + 21*260 = 6660

Анализ оптимального плана.

В оптимальный план вошла дополнительная переменная x₅. Следовательно, при реализации такого плана имеются недоиспользованные ресурсы 3-го вида в количестве 110.

Значение 0 в столбце x₁ означает, что использование x₁ - выгодно.

Значение 0 в столбце x₂ означает, что использование x₂ - выгодно.

Значение 2⁸/₁₇ в столбце x₃ означает, что теневая цена (двойственная оценка) равна y₁=2⁸/₁₇.

Значение 1¹⁰/₁₇ в столбце x₄ означает, что теневая цена (двойственная оценка) равна y₂=1¹⁰/₁₇.

Значение 0 в столбце x₅ означает, что теневая цена (двойственная оценка) равна y₃=0.

Примечание:

1. По какому методу пересчитываются симплекс-таблицы?

Используется правило прямоугольника (метод жордановских преобразований).

2. Обязательно ли каждый раз выбирать максимальное значение из индексной строки?

---

Можно не выбирать, но это может привести к зацикливанию алгоритма.

3. В индексной строке в n-ом столбце нулевое значение. Что это означает?

Нулевые значения должны соответствовать переменным, вошедшим в базис. Если в индексной строке симплексной таблицы оптимального плана находится нуль, принадлежащий свободной переменной, не вошедшей в базис, а в столбце, содержащем этот нуль, имеется хотя бы один положительный элемент, то задача имеет множество оптимальных планов.

Свободную переменную, соответствующую указанному столбцу, можно внести в базис, выполнив соответствующие этапы алгоритма. В результате будет получен второй оптимальный план с другим набором базисных переменных.
№ 21-30. Для данной задачи линейного программирования составьте двойственную, решите ее симплексным методом и укажите оптимальное решение исходной задачи.

25.

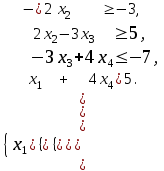
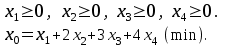
Решение:

Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.

Поскольку в правой части присутствуют отрицательные значения, умножим соответствующие строки на (-1).

Определим минимальное значение целевой функции F(X) = x₁+2x₂+3x₃+4x₄ при следующих условиях-ограничений.

-x₁+2x₂≤3

2x₂-3x₃≥5

-3x₃+4x₄≤-7

x₁+4x₄≤5

Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).

В 1-м неравенстве смысла (≤) вводим базисную переменную x₅. В 2-м неравенстве смысла (≥) вводим базисную переменную x₆ со знаком минус. В 3-м неравенстве смысла (≤) вводим базисную переменную x₇. В 4-м неравенстве смысла (≤) вводим базисную переменную x₈.

-x₁

---

+2x₂+x₅ = 3

2x₂-3x₃-x₆ = 5

-3x₃+4x₄+x₇ = -7

x₁+4x₄+x₈ = 5

Расширенная матрица системы ограничений-равенств данной задачи:

-1	2	0	0	1	0	0	0	3
0	2	-3	0	0	-1	0	0	5
0	0	-3	4	0	0	1	0	-7
1	0	0	4	0	0	0	1	5

Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x₅.

2. В качестве базовой переменной можно выбрать x₆.

Получаем новую матрицу:

-1	2	0	0	1	0	0	0	3
0	-2	3	0	0	1	0	0	-5
0	0	-3	4	0	0	1	0	-7
1	0	0	4	0	0	0	1	5

3. В качестве базовой переменной можно выбрать x₇.
4. В качестве базовой переменной можно выбрать x₈.

Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (5,6,7,8).

Выразим базисные переменные через остальные:

x₅ = x₁-2x₂+3

x₆ = 2x₂-3x₃-5

x₇ = 3x₃-4x₄-7

x₈ = -x₁-4x₄+5

Подставим их в целевую функцию:

---

Смотрите также файлы

• Охарактеризуйте основные требования к выразительному чтению педагога, дошкольника и учащегося начальной школы.docx

• Вид практикитжірибе трі Студент ваше фио факультет Сестринское делоМейіргер ісі Курс 3 группатоп 329б количество часовСаат саны 150.docx

• Программное содержание.docx

• 1тапсырма. Бастауыш білім берудегі шетелдік тжірибеге шолу теориялы материалын зерделеіз. Зерделеген материал негізінде ментальді карта зірлеіз. 1кн.docx

• Тест начат Пятница, 30 декабря 2022, 02 19 Состояние.docx