Файл: Решение Необходимо найти минимальное значение целевой функции f 2x 1 4x 2 min, при системе ограничений.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 110
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
4. Пересчет симплекс-таблицы.
Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x1 | 6 | 1 | 0 | 0 | 0 | 1 |
| x2 | 7 | 0 | 1 | 0 | 1/2 | 1/2 |
| x3 | 1 | 0 | 0 | 1 | 1/2 | -5/2 |
| F(X0) | -13 | 0 | 0 | 0 | -1/2 | -3/2 |
Представим расчет каждого элемента в виде таблицы:
| B | x1 | x2 | x3 | x4 | x5 |
| 62/5-(-2/5 • 2/5):-2/5 | 1-(0 • 2/5):-2/5 | 0-(0 • 2/5):-2/5 | 2/5-(-2/5 • 2/5):-2/5 | 1/5-(-1/5 • 2/5):-2/5 | 0-(1 • 2/5):-2/5 |
| 71/5-(-2/5 • 1/5):-2/5 | 0-(0 • 1/5):-2/5 | 1-(0 • 1/5):-2/5 | 1/5-(-2/5 • 1/5):-2/5 | 3/5-(-1/5 • 1/5):-2/5 | 0-(1 • 1/5):-2/5 |
| -2/5 : -2/5 | 0 : -2/5 | 0 : -2/5 | -2/5 : -2/5 | -1/5 : -2/5 | 1 : -2/5 |
| -133/5-(-2/5 • -3/5):-2/5 | 0-(0 • -3/5):-2/5 | 0-(0 • -3/5):-2/5 | -3/5-(-2/5 • -3/5):-2/5 | -4/5-(-1/5 • -3/5):-2/5 | 0-(1 • -3/5):-2/5 |
Решение получилось целочисленным. Нет необходимости применять метод Гомори.
Оптимальный целочисленный план можно записать так:
x1 = 6, x2 = 7
F(X) = 1*6 + 1*7 = 13
Графический метод
Необходимо найти максимальное значение целевой функции F = x1+x2 → max, при системе ограничений:
3x1-x2≤12, (1)
-x1+2x2≤8, (2)
x1 ≥ 0, (3)
x2 ≥ 0, (4)
где x1, x2 - целые числа.
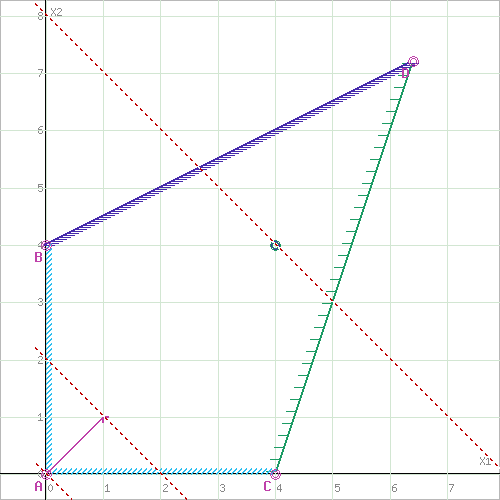
Шаг №1. Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).
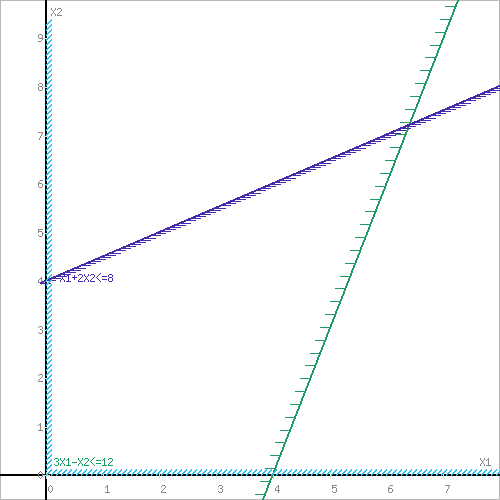
или
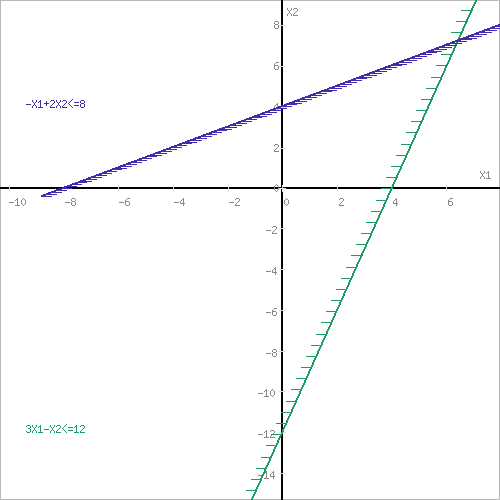
Шаг №2. Границы области допустимых решений.
Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.
Обозначим границы области многоугольника решений.
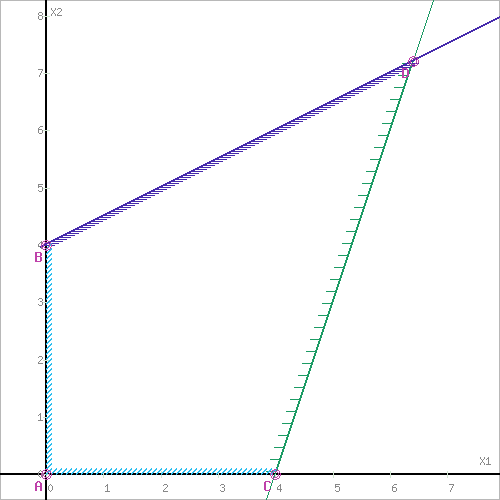
Шаг №3. Рассмотрим целевую функцию задачи F = x1+x2 → max.
Построим прямую, отвечающую значению функции F = x1+x2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (1;1). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.
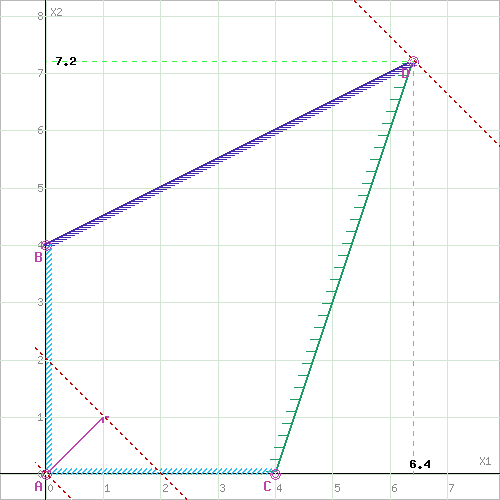
Прямая F(x) = const пересекает область в точке D. Так как точка D получена в результате пересечения прямых (1) и (2), то ее координаты удовлетворяют уравнениям этих прямых:
3x1-x2=12
-x1+2x2=8
Решив систему уравнений, получим: x1 = 6.4, x2 = 7.2
Откуда найдем максимальное значение целевой функции:
F(X) = 1*6.4 + 1*7.2 = 13.6
Решение получилось не целочисленным.
Множество допустимых решений задачи с отмеченными на нем целочисленными точками представлено на рис. 5.
Перемещение линии уровня целевой функции F(X) в направлении, задаваемом ее градиентом, показывает, что наибольшее значение F(X)=8 она примет в точке (4, 4).
№ 41-50. На трех базах А1, А2, А3 находится однородный груз вколичествесоответственно a1, a2, a3 тонн. Этот груз необходимоперевести на четыре предприятий В1, В2, В3, В4, В5, потребности которых соответственно равны b1, b2, b3, b4 тонн. Стоимость перевозки одной тонны груза с базы Аi на предприятие Вj составляет cij рублей. Эти стоимости заданы в матрице С, запасы грузов на базах (в тоннах) заданы в матрице А, а потребности предприятий (в тоннах) – в матрице В.
Составьте план перевозок груза на предприятия таким образом, чтобы их общая стоимость была наименьшей. Сравните стоимости перевозок в исходном и оптимальном планах.
47.С =
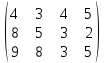 , А =
, А =  , В =
, В = 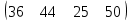 .
.Решение:
Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов
| | B1 | B2 | B3 | B4 | Запасы |
| A1 | 4 | 3 | 4 | 5 | 55 |
| A2 | 8 | 5 | 3 | 2 | 60 |
| A3 | 9 | 8 | 3 | 5 | 48 |
| Потребности | 36 | 44 | 25 | 50 | |
Проверим необходимое и достаточное условие разрешимости задачи.
∑a = 55 + 60 + 48 = 163
∑b = 36 + 44 + 25 + 50 = 155
Как видно, суммарная потребность груза в пунктах назначения меньше запасов груза на базах. Следовательно, модель исходной транспортной задачи является открытой. Чтобы получить закрытую модель, введем дополнительную (фиктивную) потребность, равной 8 (163—155). Тарифы перевозки единицы груза к этому потребителю полагаем равны нулю.
Занесем исходные данные в распределительную таблицу.
| | B1 | B2 | B3 | B4 | B5 | Запасы |
| A1 | 4 | 3 | 4 | 5 | 0 | 55 |
| A2 | 8 | 5 | 3 | 2 | 0 | 60 |
| A3 | 9 | 8 | 3 | 5 | 0 | 48 |
| Потребности | 36 | 44 | 25 | 50 | 8 | |
Этап I. Поиск первого опорного плана.
1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.
Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел ai, или bj.
Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя.
Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают
, пока все запасы не будут распределены, а потребности удовлетворены.
Искомый элемент равен c24=2. Для этого элемента запасы равны 60, потребности 50. Поскольку минимальным является 50, то вычитаем его.
x24 = min(60,50) = 50.
| 4 | 3 | 4 | x | 0 | 55 |
| 8 | 5 | 3 | 2 | 0 | 60 - 50 = 10 |
| 9 | 8 | 3 | x | 0 | 48 |
| 36 | 44 | 25 | 50 - 50 = 0 | 8 | |
Искомый элемент равен c12=3. Для этого элемента запасы равны 55, потребности 44. Поскольку минимальным является 44, то вычитаем его.
x12 = min(55,44) = 44.
| 4 | 3 | 4 | x | 0 | 55 - 44 = 11 |
| 8 | x | 3 | 2 | 0 | 10 |
| 9 | x | 3 | x | 0 | 48 |
| 36 | 44 - 44 = 0 | 25 | 0 | 8 | |