Файл: Курсовая работа по дисциплине антенны и распространение радиоволн.docx
Добавлен: 07.11.2023
Просмотров: 63
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2.1. Расчёт и выбор геометрических параметров спиральной антенны

(2.1)
Известны следующие геометрические соотношения для винтовой линии, которой является основной составляющей спиральной антенны:
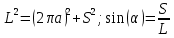

(2.2)
Подставляя значение длины витка (1.1), найденное из условия максимального КНД, в выражение для геометрического соотношения (2.1), получим:
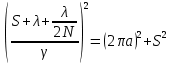
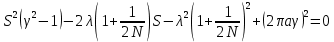
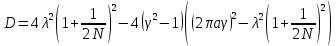
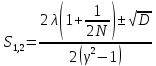

Таким образом, экспериментально подобрав оптимальное значение радиуса, можно найти фазовую скорость собственной волны в цилиндрической антенне (Рис. 1.5) и, соответственно, значение шага спирали, при котором обеспечивается максимальный КНД, а следовательно, и определить все геометрические размеры спирали.
Как уже было упомянуто в пункте 1.2 главы 1 диаметр экрана слабо влияет на входное сопротивление при >0,4 λ, а диаграмма направленности и поляризационная характеристика наиболее стабильны в диапазоне частот при
>0,4 λ, а диаграмма направленности и поляризационная характеристика наиболее стабильны в диапазоне частот при  (0,6 ... 0,7) λ, таким образом целесообразно выбрать
(0,6 ... 0,7) λ, таким образом целесообразно выбрать  = 0,6 λ. А также радиус проводника спирали выбирается в пределах
= 0,6 λ. А также радиус проводника спирали выбирается в пределах  = (0,01 …0,2) λ.
= (0,01 …0,2) λ.
Так как при наличии 11 витков в спиральной антенне её КНД не изменяется, то целесообразно для минимизации габаритов и достижения поставленной задачи, использовать именно это количество витков.
2.2. Расчёт характеристик спиральной антенны

(2.3)
Входное сопротивление спиральной антенны удовлетворительно можно рассчитать через формулу Крауса:
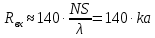

(2.4)
КНД спиральной антенны можно рассчитать по следующей формуле:
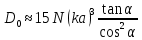

(2.5)
Ширину ДН по уровню половинной мощности можно оценить по формуле:
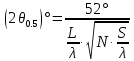

(2.6)
Как показывают исследования, ДН спиральной антенны и системы таких антенн в плоскостях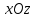 и
и 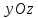 различаются мало и только в области боковых лепестков, поэтому для вычисления КНД можно использовать формулу, учитывающую осевую симметрию ДН:
различаются мало и только в области боковых лепестков, поэтому для вычисления КНД можно использовать формулу, учитывающую осевую симметрию ДН:
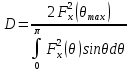
Для расчёта диаграмм направленности цилиндрической спиральной антенны в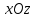 плоскости используются приведенные ниже формулы:
плоскости используются приведенные ниже формулы:
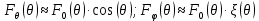 ВЫ
ВЫ
 В
В 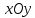 плоскости используются формулы:
плоскости используются формулы:
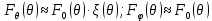 ,
,
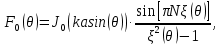
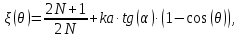
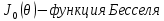 ;
; 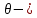 угол отклонения от продольной оси антенны;
угол отклонения от продольной оси антенны; 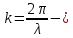 волновое число.
волновое число.
Диаграмма направленности одиночной спиральной антенны по мощности:

(2.7)
в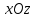 плоскости:
плоскости: 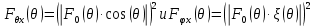
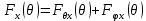

(2.8)
в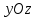 плоскости:
плоскости: 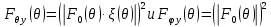
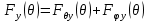

(2.9)
Усредненная диаграмма направленности по мощности:
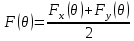
Глава 3
РАСЧЁТНА ЧАСТЬ И МОДЕЛИРОВАНИЕ
3.1. Подбор геометрических параметров спиральной антенны

Рис. 3.1.
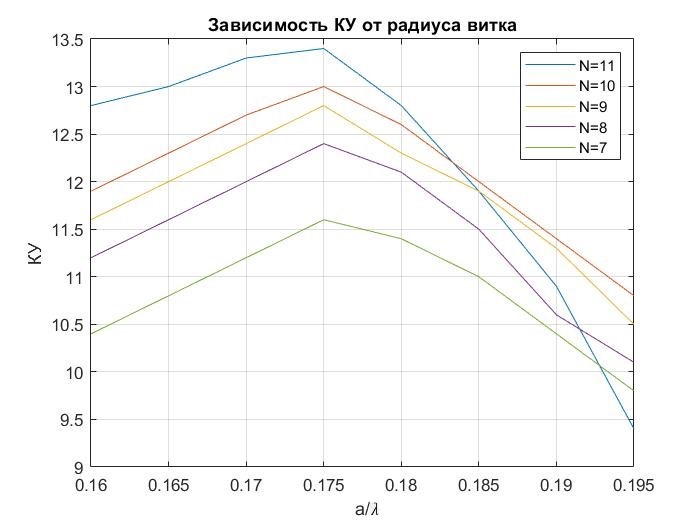 В процессе моделирования была получена следующая зависимость КУ от радиуса витка, для различного числа витков
В процессе моделирования была получена следующая зависимость КУ от радиуса витка, для различного числа витков 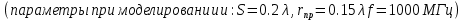 :
:
Таким образом максимальный КУ достигается при количестве витков: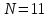 и радиусе витка:
и радиусе витка: 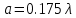 . КУ при этом достигает значения 13.41 дБ. Соответственно по графику зависимости фазовой скорости собственной волны
. КУ при этом достигает значения 13.41 дБ. Соответственно по графику зависимости фазовой скорости собственной волны  от величины
от величины 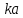 (Рис. 1.5) определяем значение замедления волны в спирали: для
(Рис. 1.5) определяем значение замедления волны в спирали: для 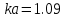 получаем
получаем 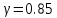 .
.
Зная значение числа витков и замедления волны, находим величину оптимального шага спирали, при котором достигается наибольший КУ из формулы (2.2)
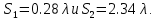
Значение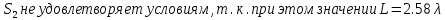 ., которое не позволит добиться осевого излучения.
., которое не позволит добиться осевого излучения.
Оптимальным является значение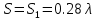 .
.
Для этого шага спирали длина витка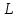 :
:
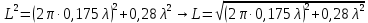 =
= 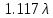
Угол намотки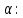
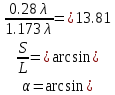
Входное сопротивление спиральной антенны удовлетворительно можно рассчитать через формулу Крауса:
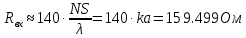
КНД спиральной антенны можно рассчитать по следующей формуле:
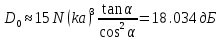
При моделировании также было подобрано оптимальное значение радиуса провода, при котором достигается максимальный КУ, шаг сетки расстояние до рефлектора и превышение рефлектором размеров антенны.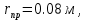 шаг сетки:
шаг сетки: 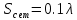 , расстояние до рефлектора:
, расстояние до рефлектора: 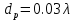 , превышение рефлектором размеров антенны:
, превышение рефлектором размеров антенны: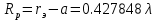

Таким образом получаем следующие геометрические параметры антенны:
Таблица 3.1. Геометрические параметры
3.2. Построение диаграмм направленности на частотах диапазона спиральной антенны
Расчёт диаграммы направленности по мощности производится с помощью формул, которые были описаны в пункте 2.2. главы 2.
Частота 1000МГц
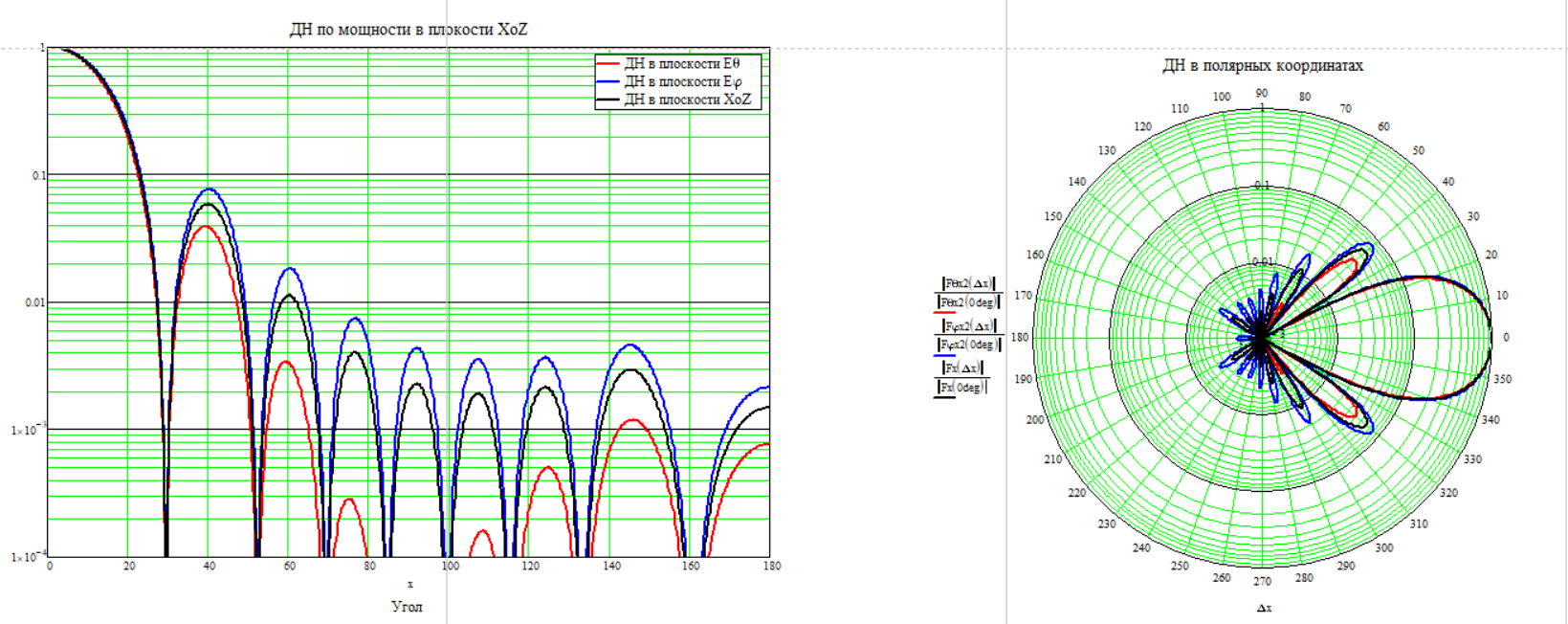
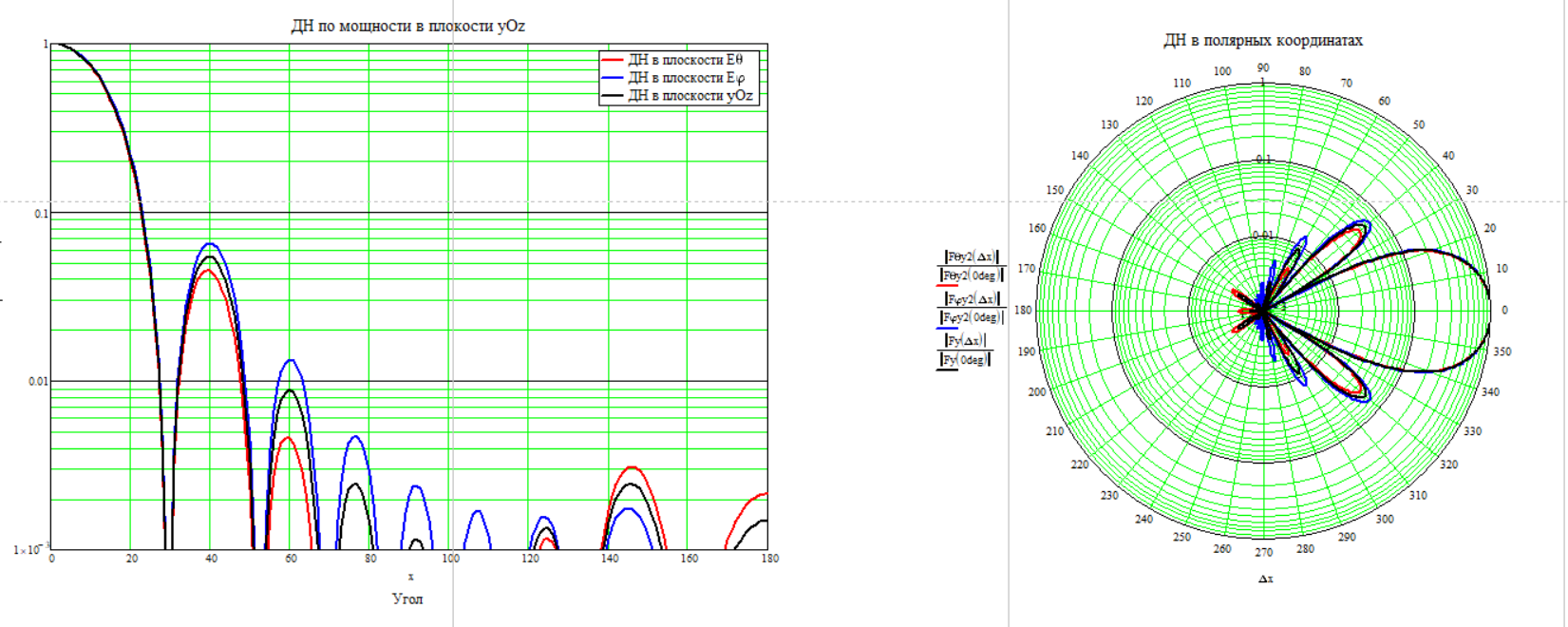
Для расчёта КНД по диаграмме направленности воспользуемся формулой (2.6)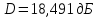
Частота 1250 МГц
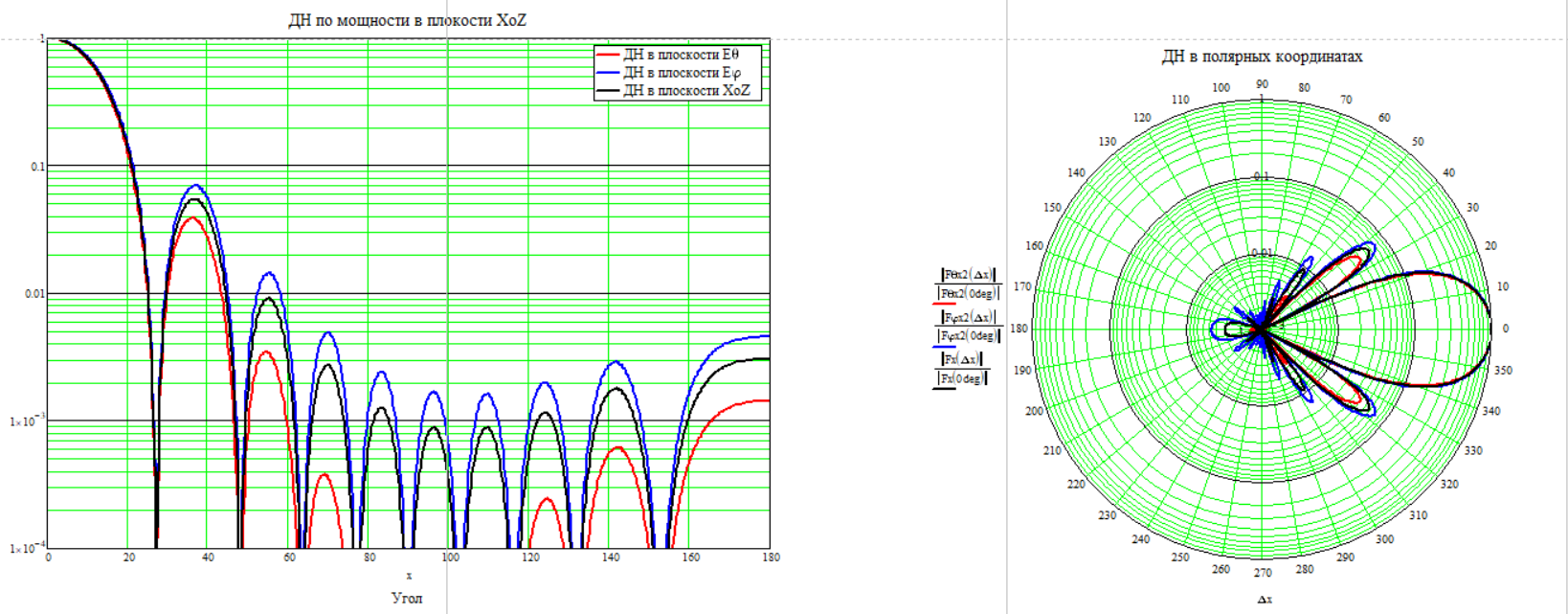
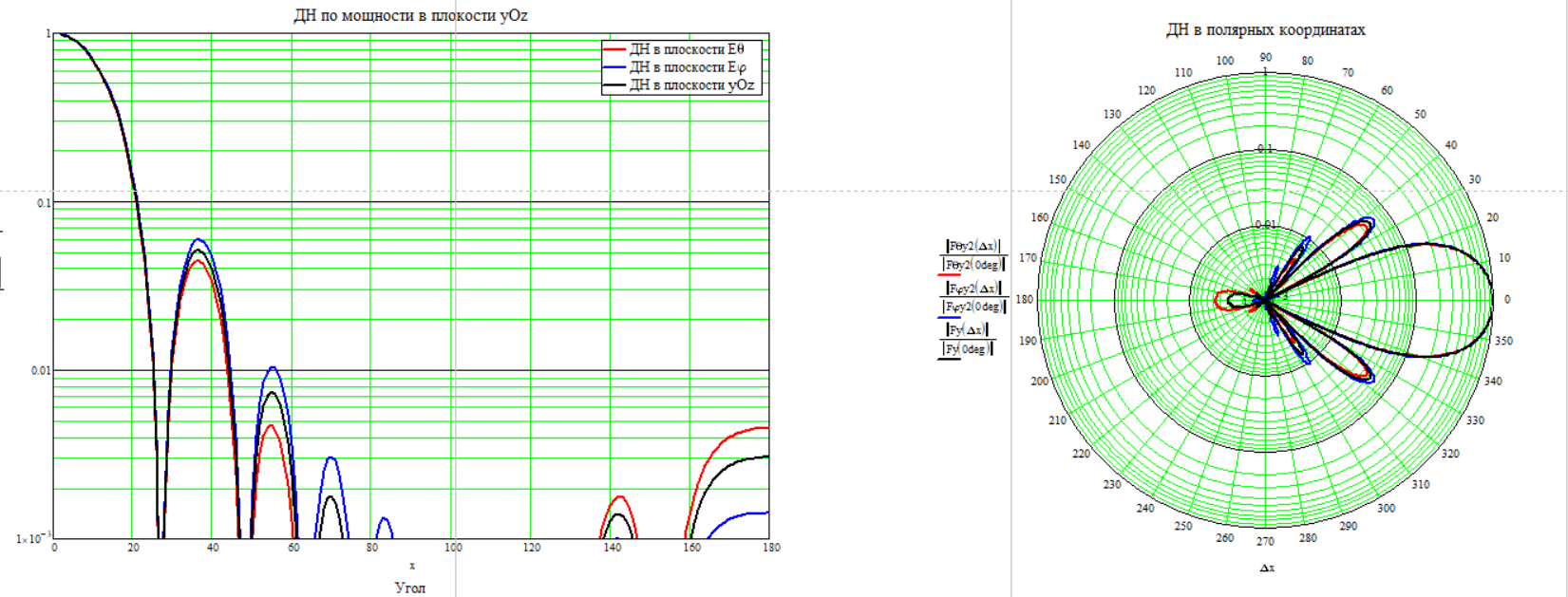
Для расчёта КНД по диаграмме направленности воспользуемся формулой (2.6)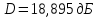
Частота 1500 МГц
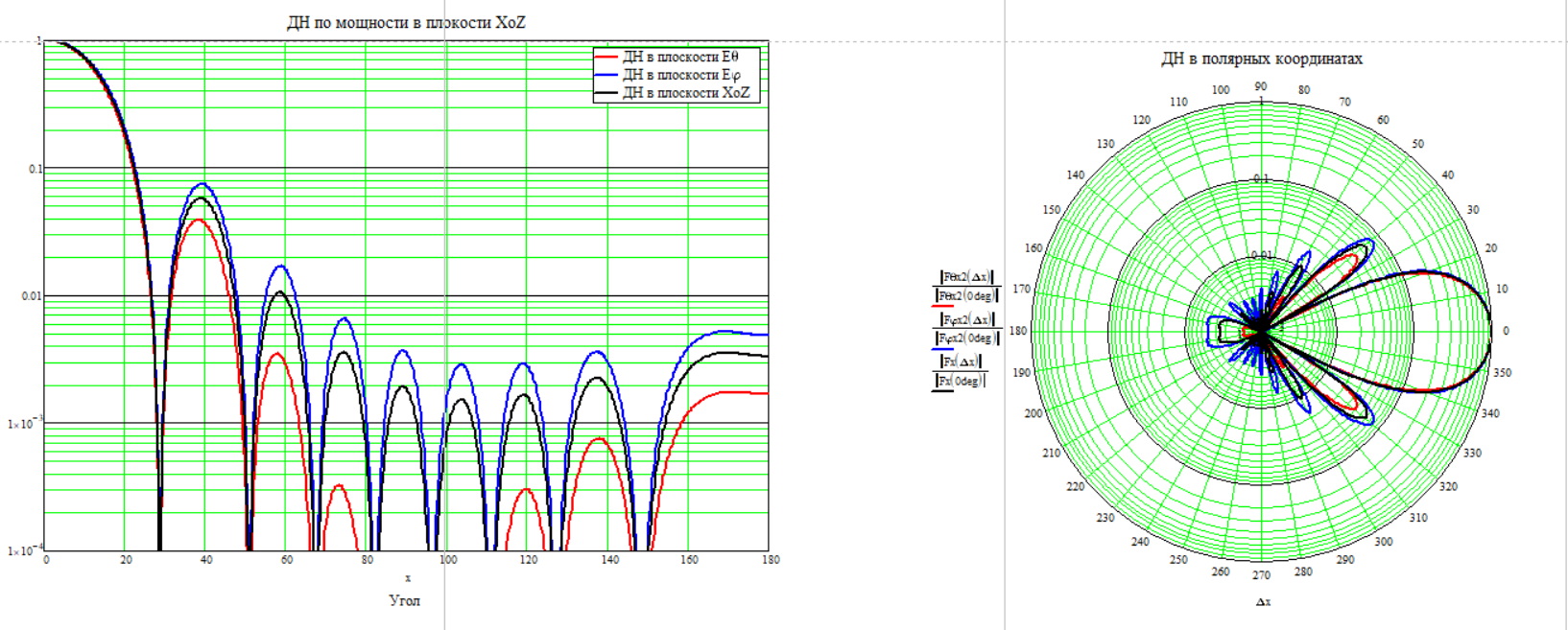
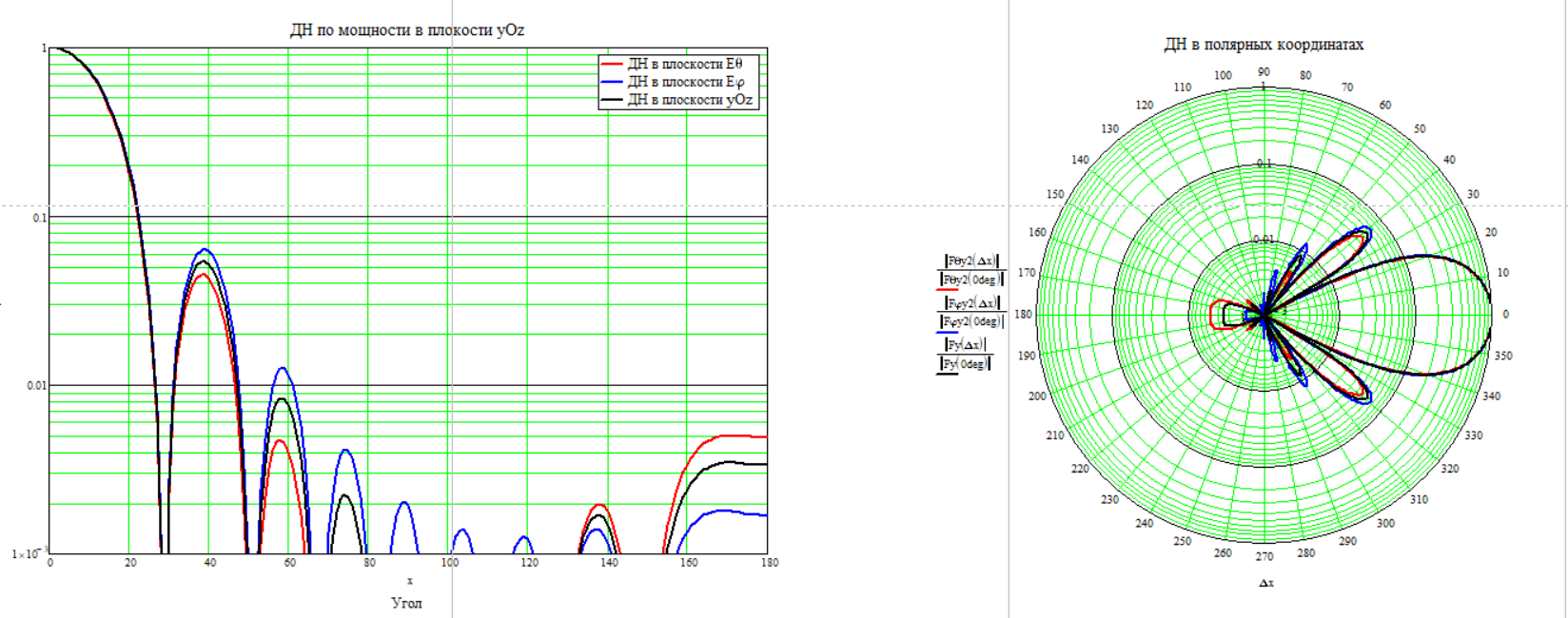
Для расчёта КНД по диаграмме направленности воспользуемся формулой (2.6)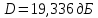
Частота 1750 МГц
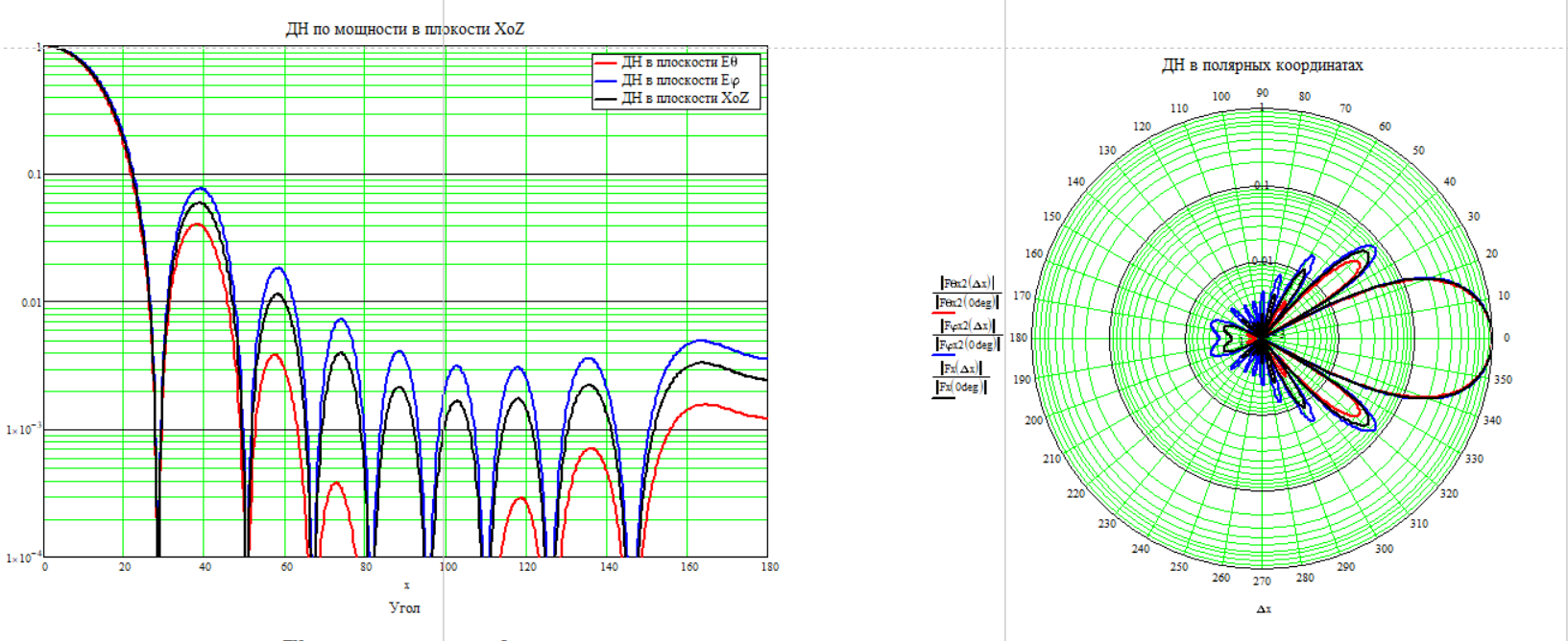
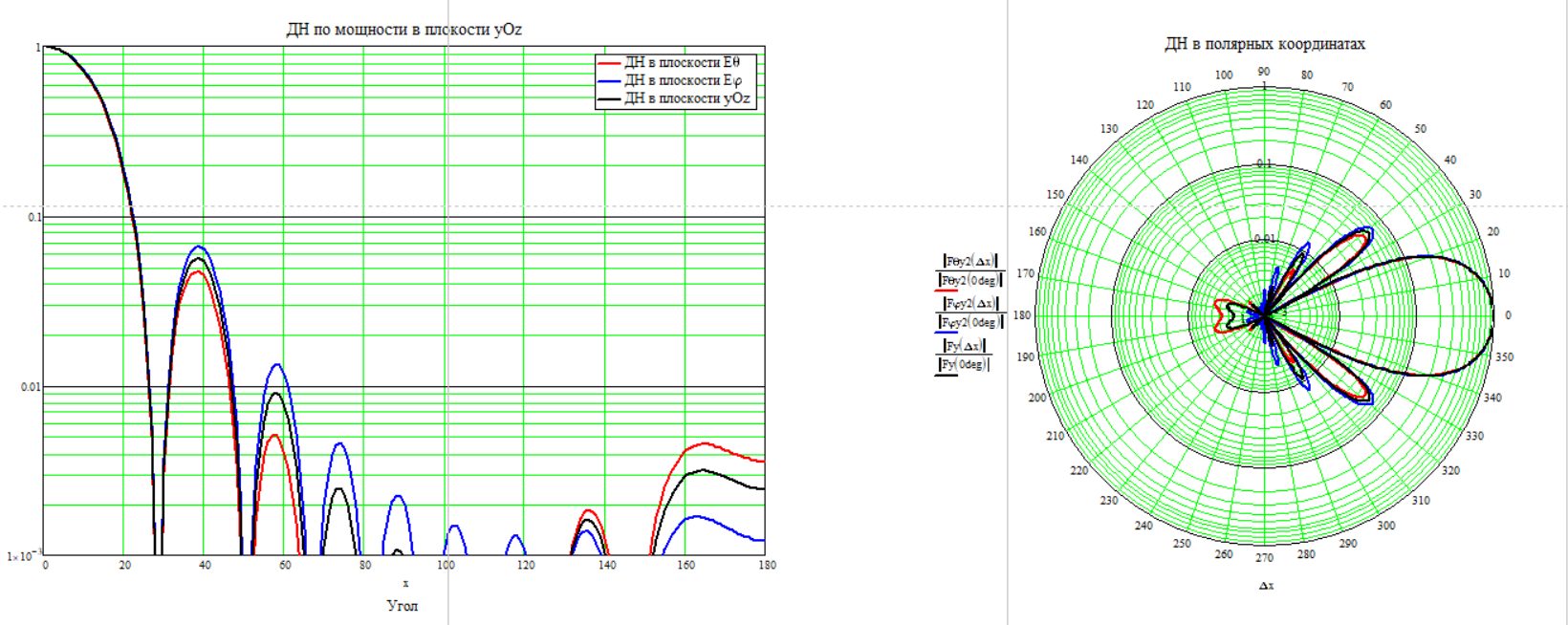
Для расчёта КНД по диаграмме направленности воспользуемся формулой (2.6)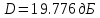
Частота 2000 МГц
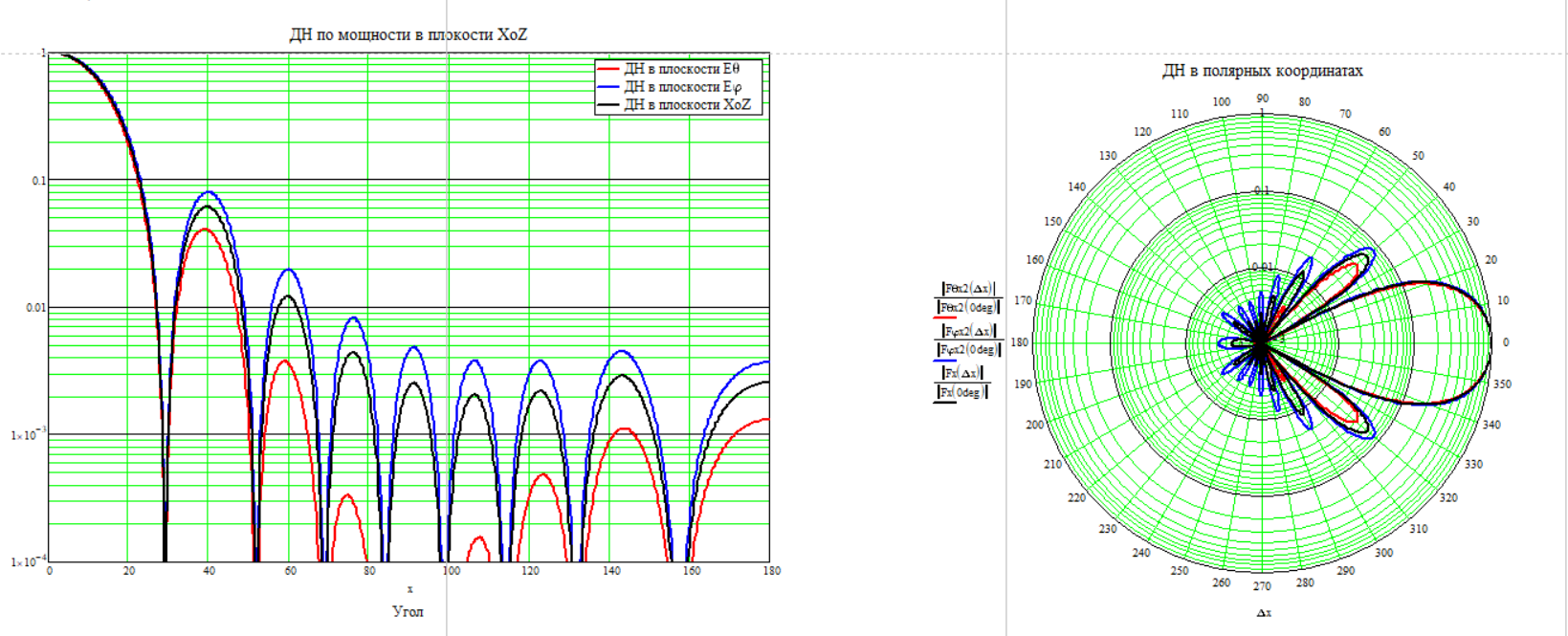
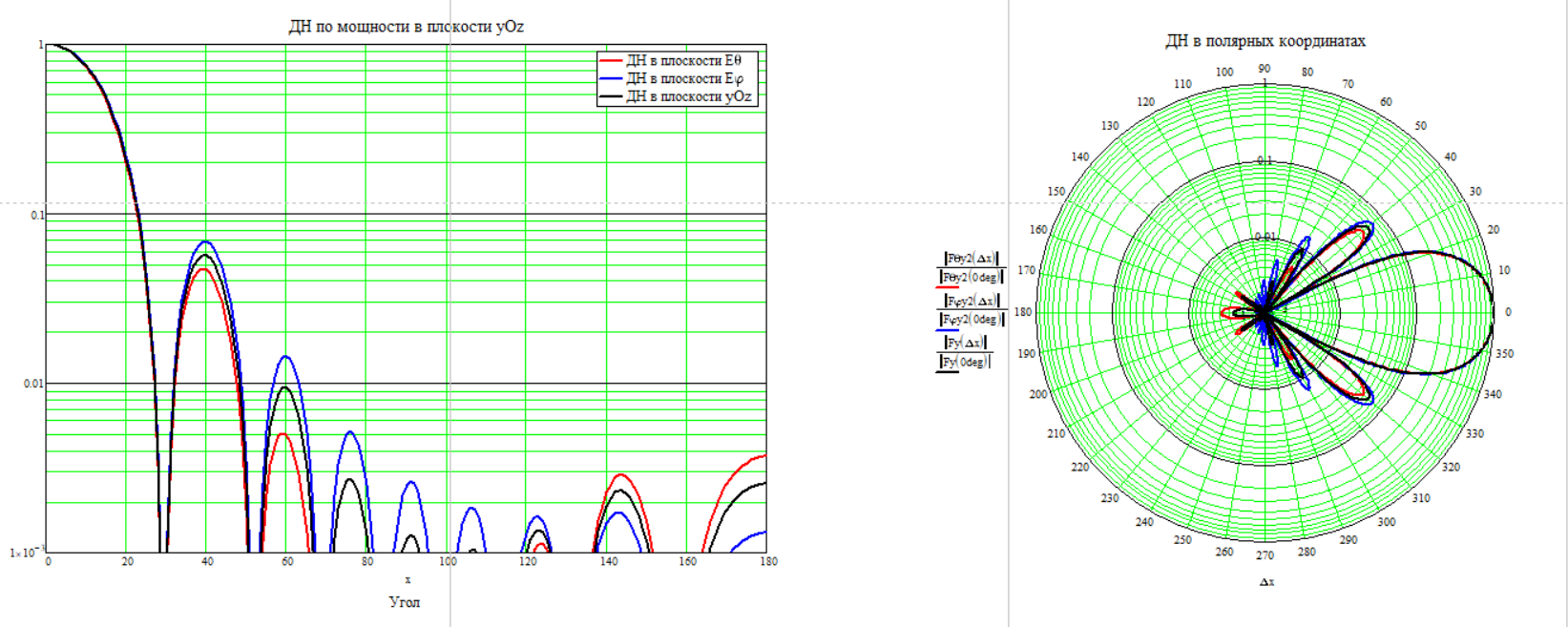
Для расчёта КНД по диаграмме направленности воспользуемся формулой (2.6)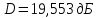
3.3. Моделирование спиральной антенны
Для рассчитанных оптимальных геометрических размеров была реализована модель в программе MANAGAL.
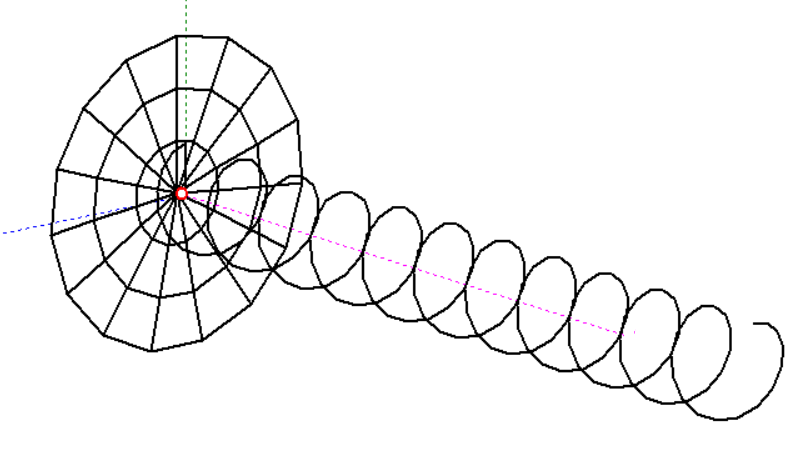 Далее представлены диаграммы направленности на частотах 1000, 1250, 1750 и 2000 МГц соответственно:
Далее представлены диаграммы направленности на частотах 1000, 1250, 1750 и 2000 МГц соответственно:
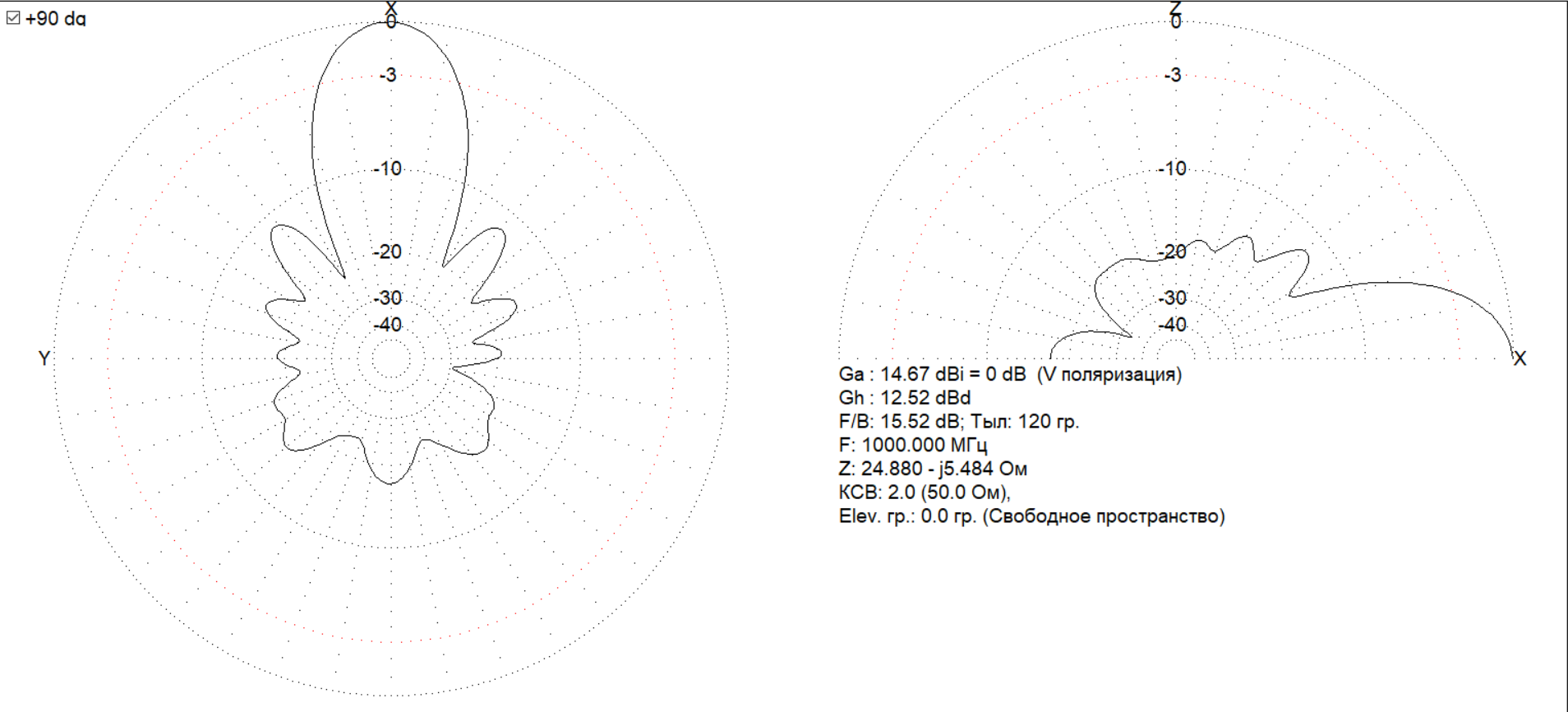
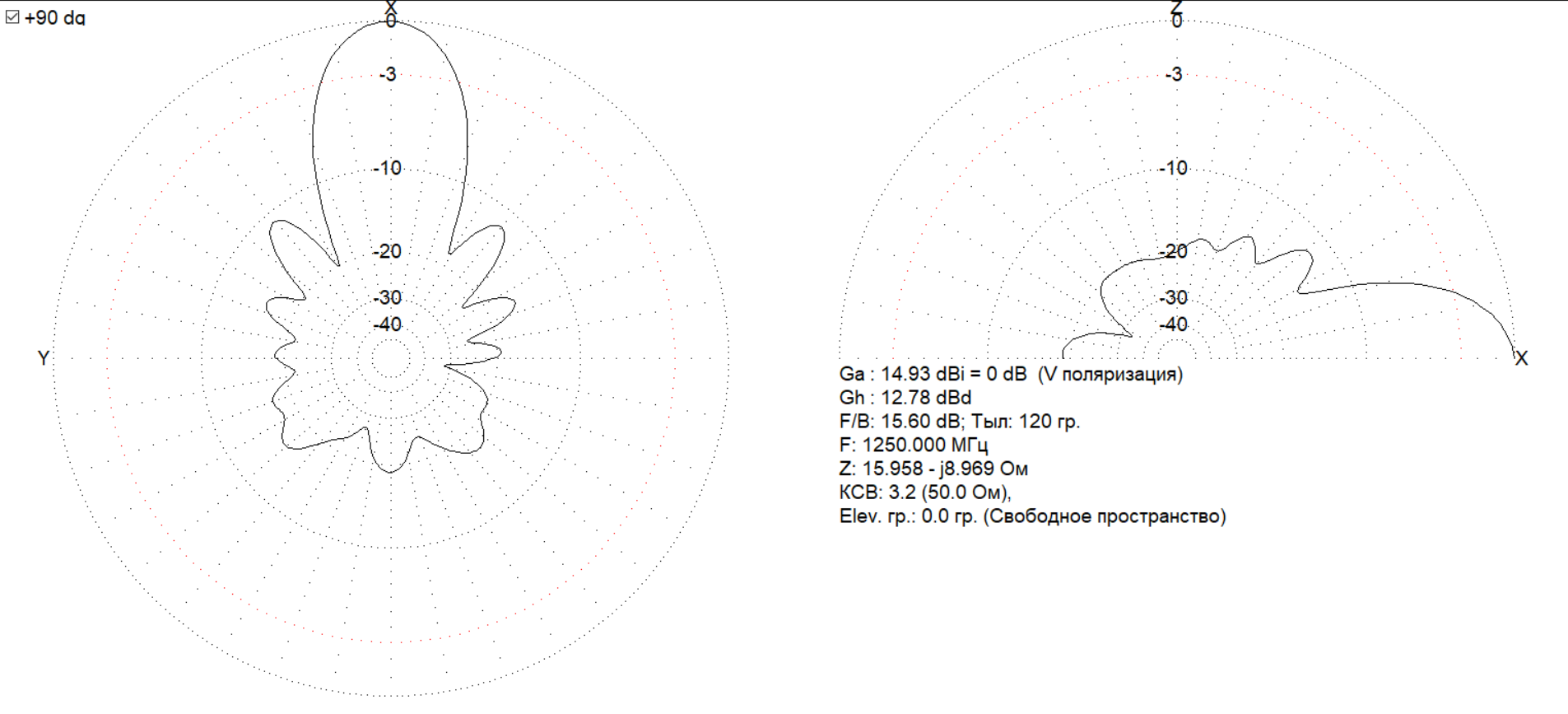
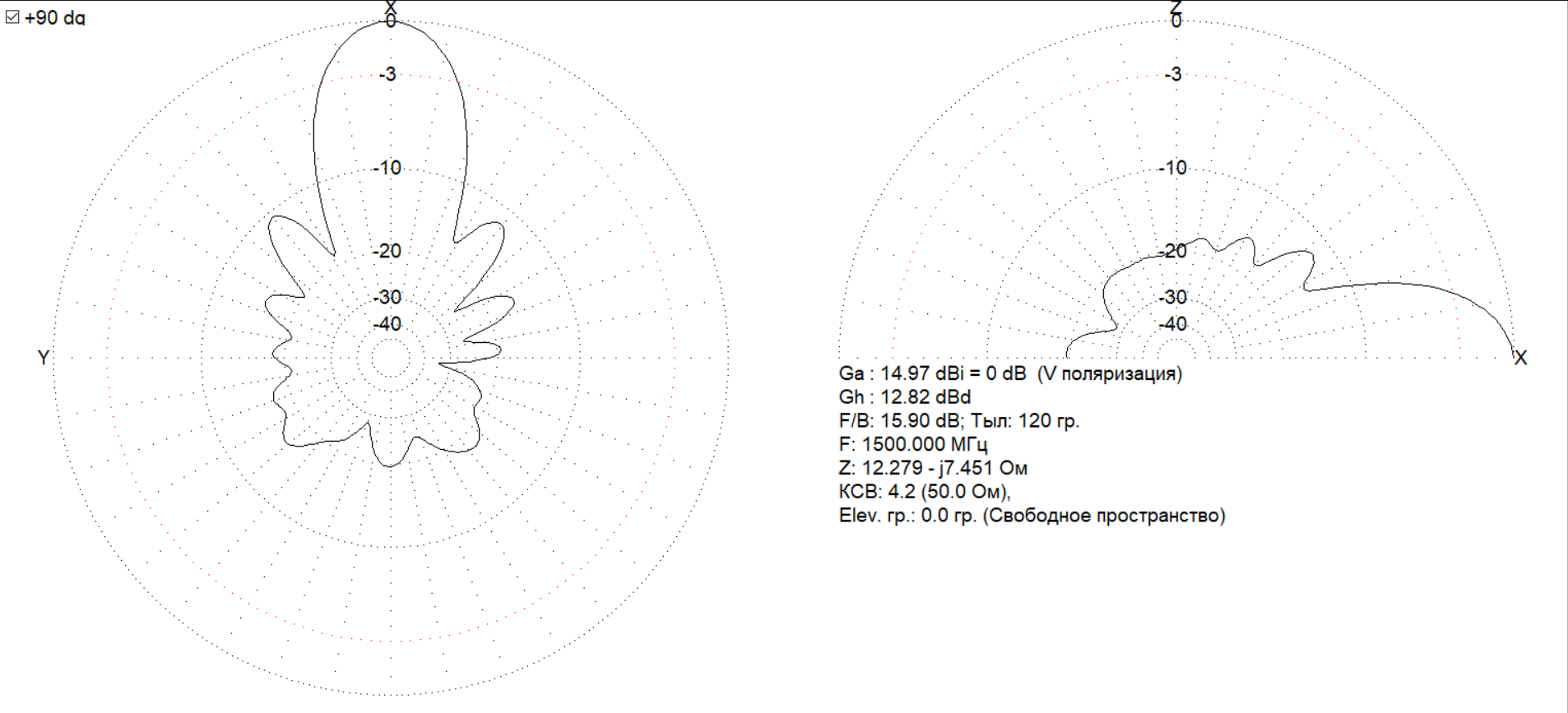
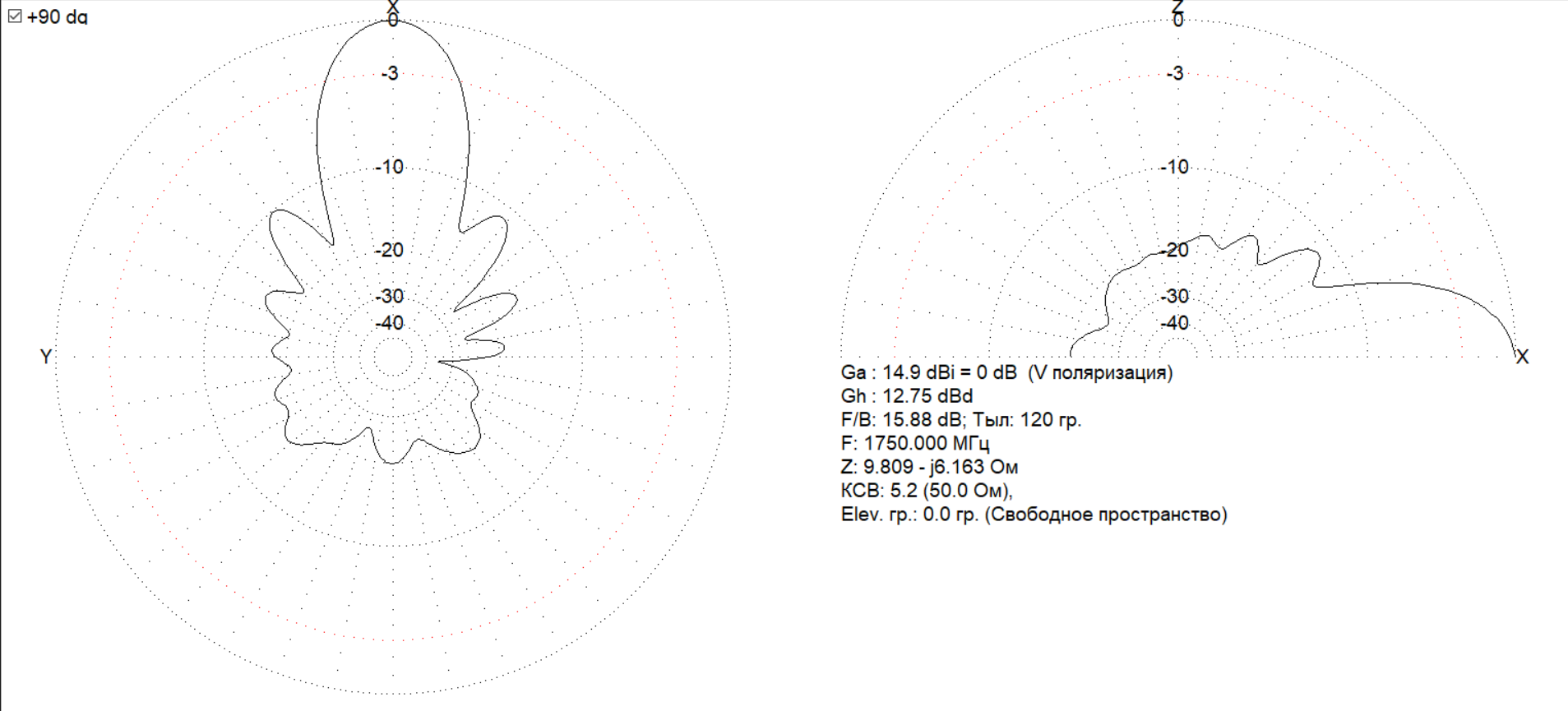
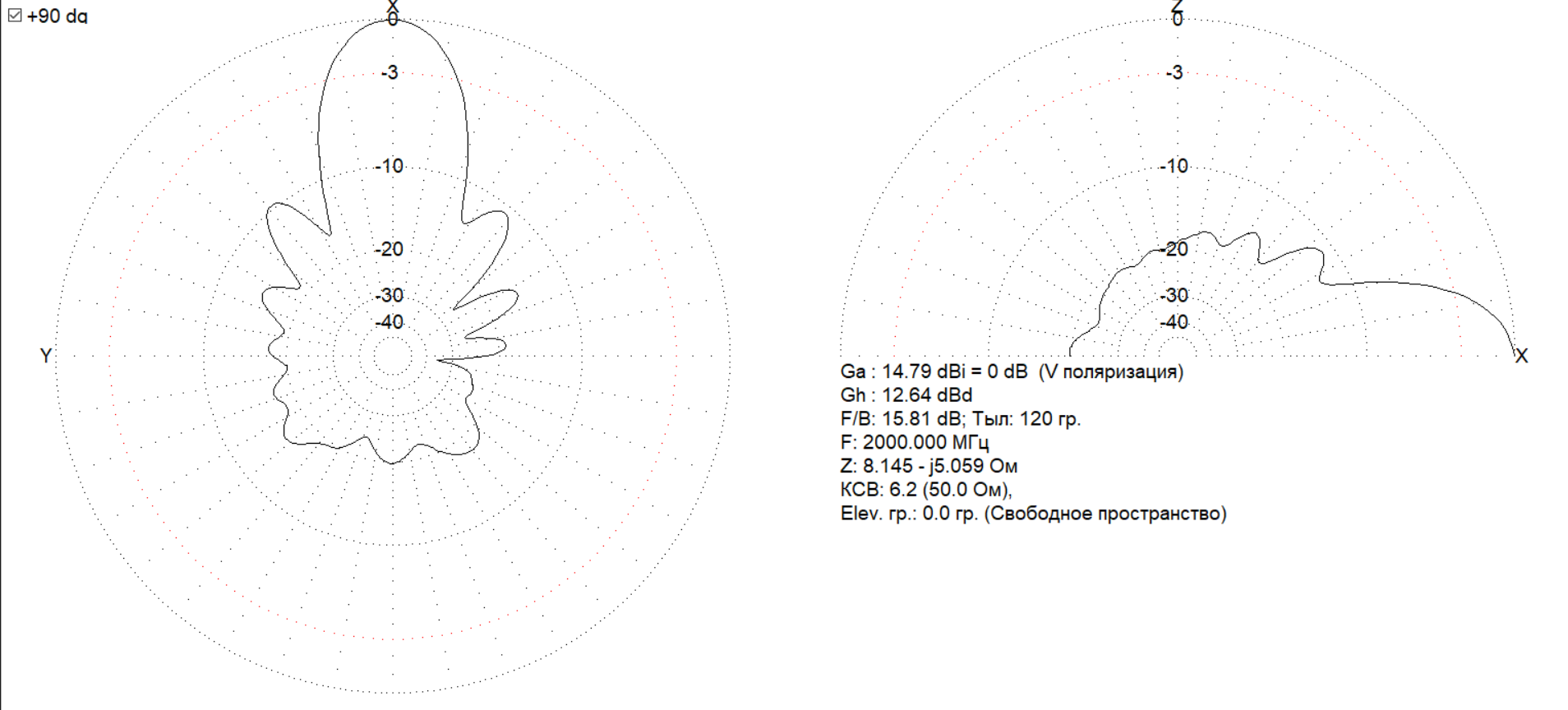
3.4. Сопоставление теоретических расчетов и результатов моделирования спиральной антенны
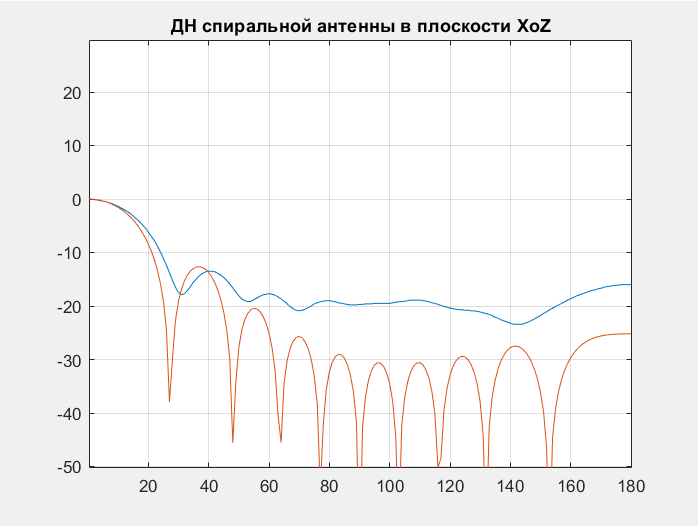
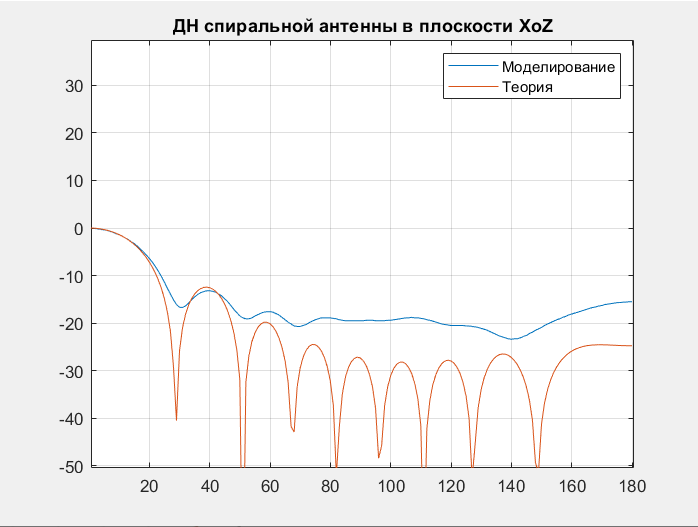
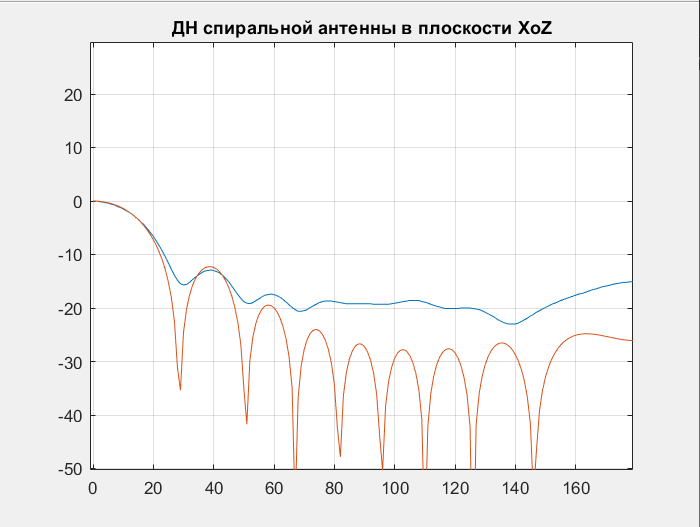
Далее приведено сопоставление ДН полученных теоретически и в процессе моделирования:
F=1000МГц
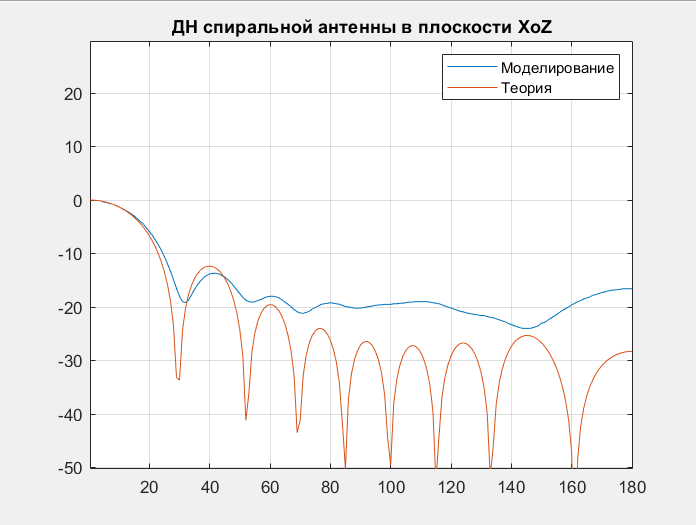

F=1250МГц F=1500МГц


F=1750МГц F=2000МГц
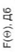


Заключение
В ходе выполнения курсовой работы были изучены основные этапы расчета параметров и дальнейшей проектировки цилиндрической спиральной антенны.
Также были получены знания и практические навыки, которые позволили решить задачу по разработке антенны указанного типа согласно полученному техническому заданию.
Были подобраны оптимальный параметры цилиндрической спиральной антенны, для получения осевого излучения и максимального КУ. Таким образом, для реализации заданного технического задания использование исследованной конструкции антенны является целесообразным.
1. Сомов А. М., Кабетов Р. В. Проектирование антенно-фидерных устройств. Учебное пособие для вузов / Под ред. Профессора А. М. Сомова. – М.: Горячая линия – Телеком, 2016. – 500с.: ил.
2. Юрцев О. А., Рунов А.В., Казарин А.Н. Спиральные антенны. – М.: Сов. Радио, 1974. – 224 с.
3. Айзенберг Г.З. и др. Антенны УКВ. Под ред. Г.З. Айзенберга. В 2-х ч.
Ч. 2. М., “Связь”, 1977 – 228 с.
4. Драбкин А. Л. и др., Д72 Антенно-фидерные устройства. Изд. 2-е, доп. «Сов. радио», 1974. 536 с. с ил.

(2.1)
Известны следующие геометрические соотношения для винтовой линии, которой является основной составляющей спиральной антенны:
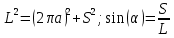

(2.2)
Подставляя значение длины витка (1.1), найденное из условия максимального КНД, в выражение для геометрического соотношения (2.1), получим:
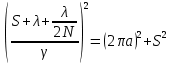
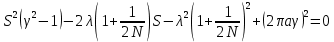
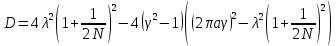
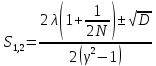

Как уже было упомянуто в пункте 1.2 главы 1 диаметр экрана слабо влияет на входное сопротивление при
 >0,4 λ, а диаграмма направленности и поляризационная характеристика наиболее стабильны в диапазоне частот при
>0,4 λ, а диаграмма направленности и поляризационная характеристика наиболее стабильны в диапазоне частот при  (0,6 ... 0,7) λ, таким образом целесообразно выбрать
(0,6 ... 0,7) λ, таким образом целесообразно выбрать  = 0,6 λ. А также радиус проводника спирали выбирается в пределах
= 0,6 λ. А также радиус проводника спирали выбирается в пределах  = (0,01 …0,2) λ.
= (0,01 …0,2) λ.Так как при наличии 11 витков в спиральной антенне её КНД не изменяется, то целесообразно для минимизации габаритов и достижения поставленной задачи, использовать именно это количество витков.
2.2. Расчёт характеристик спиральной антенны

(2.3)
Входное сопротивление спиральной антенны удовлетворительно можно рассчитать через формулу Крауса:
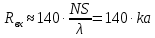

(2.4)
КНД спиральной антенны можно рассчитать по следующей формуле:
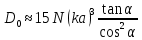

(2.5)
Ширину ДН по уровню половинной мощности можно оценить по формуле:
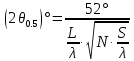

(2.6)
Как показывают исследования, ДН спиральной антенны и системы таких антенн в плоскостях
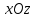 и
и 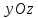 различаются мало и только в области боковых лепестков, поэтому для вычисления КНД можно использовать формулу, учитывающую осевую симметрию ДН:
различаются мало и только в области боковых лепестков, поэтому для вычисления КНД можно использовать формулу, учитывающую осевую симметрию ДН: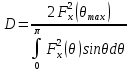
Для расчёта диаграмм направленности цилиндрической спиральной антенны в
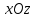 плоскости используются приведенные ниже формулы:
плоскости используются приведенные ниже формулы: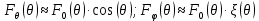 ВЫ
ВЫ В
В 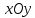 плоскости используются формулы:
плоскости используются формулы: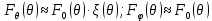 ,
,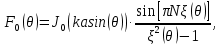
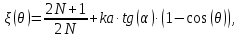
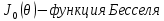 ;
; 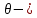 угол отклонения от продольной оси антенны;
угол отклонения от продольной оси антенны; 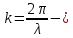 волновое число.
волновое число.Диаграмма направленности одиночной спиральной антенны по мощности:

(2.7)
в
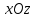 плоскости:
плоскости: 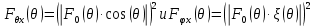
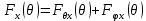

(2.8)
в
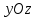 плоскости:
плоскости: 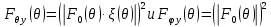
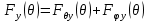

(2.9)
Усредненная диаграмма направленности по мощности:
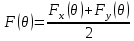
Глава 3
РАСЧЁТНА ЧАСТЬ И МОДЕЛИРОВАНИЕ
3.1. Подбор геометрических параметров спиральной антенны

Рис. 3.1.
 В процессе моделирования была получена следующая зависимость КУ от радиуса витка, для различного числа витков
В процессе моделирования была получена следующая зависимость КУ от радиуса витка, для различного числа витков 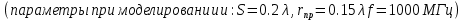 :
:Таким образом максимальный КУ достигается при количестве витков:
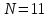 и радиусе витка:
и радиусе витка: 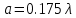 . КУ при этом достигает значения 13.41 дБ. Соответственно по графику зависимости фазовой скорости собственной волны
. КУ при этом достигает значения 13.41 дБ. Соответственно по графику зависимости фазовой скорости собственной волны  от величины
от величины 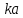 (Рис. 1.5) определяем значение замедления волны в спирали: для
(Рис. 1.5) определяем значение замедления волны в спирали: для 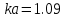 получаем
получаем 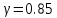 .
. Зная значение числа витков и замедления волны, находим величину оптимального шага спирали, при котором достигается наибольший КУ из формулы (2.2)
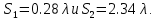
Значение
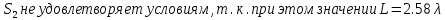 ., которое не позволит добиться осевого излучения.
., которое не позволит добиться осевого излучения. Оптимальным является значение
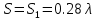 .
.Для этого шага спирали длина витка
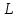 :
: 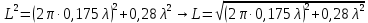 =
= 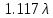
Угол намотки
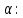
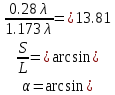
Входное сопротивление спиральной антенны удовлетворительно можно рассчитать через формулу Крауса:
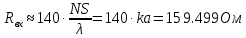
КНД спиральной антенны можно рассчитать по следующей формуле:
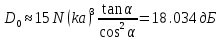
При моделировании также было подобрано оптимальное значение радиуса провода, при котором достигается максимальный КУ, шаг сетки расстояние до рефлектора и превышение рефлектором размеров антенны.
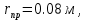 шаг сетки:
шаг сетки: 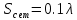 , расстояние до рефлектора:
, расстояние до рефлектора: 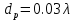 , превышение рефлектором размеров антенны:
, превышение рефлектором размеров антенны: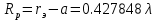

| N, шт | 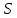 , ,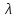 | 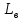 , , 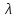 | 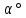 | 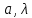 |  , м , м | 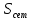 , , 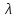 | 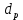 , , 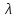 | 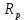 , , 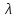 |
| 11 | 0.28 | 1.117 | 13.81 | 0.175 | 0.08 | 0.1 | 0.03 | 0.43 |
Таблица 3.1. Геометрические параметры
3.2. Построение диаграмм направленности на частотах диапазона спиральной антенны
Расчёт диаграммы направленности по мощности производится с помощью формул, которые были описаны в пункте 2.2. главы 2.
Частота 1000МГц


Для расчёта КНД по диаграмме направленности воспользуемся формулой (2.6)
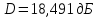
Частота 1250 МГц


Для расчёта КНД по диаграмме направленности воспользуемся формулой (2.6)
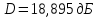
Частота 1500 МГц


Для расчёта КНД по диаграмме направленности воспользуемся формулой (2.6)
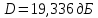
Частота 1750 МГц


Для расчёта КНД по диаграмме направленности воспользуемся формулой (2.6)
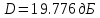
Частота 2000 МГц


Для расчёта КНД по диаграмме направленности воспользуемся формулой (2.6)
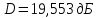
3.3. Моделирование спиральной антенны
Для рассчитанных оптимальных геометрических размеров была реализована модель в программе MANAGAL.
 Далее представлены диаграммы направленности на частотах 1000, 1250, 1750 и 2000 МГц соответственно:
Далее представлены диаграммы направленности на частотах 1000, 1250, 1750 и 2000 МГц соответственно:




3.4. Сопоставление теоретических расчетов и результатов моделирования спиральной антенны
Далее приведено сопоставление ДН полученных теоретически и в процессе моделирования:
F=1000МГц

F=1250МГц F=1500МГц


F=1750МГц F=2000МГц


Заключение
В ходе выполнения курсовой работы были изучены основные этапы расчета параметров и дальнейшей проектировки цилиндрической спиральной антенны.
Также были получены знания и практические навыки, которые позволили решить задачу по разработке антенны указанного типа согласно полученному техническому заданию.
Были подобраны оптимальный параметры цилиндрической спиральной антенны, для получения осевого излучения и максимального КУ. Таким образом, для реализации заданного технического задания использование исследованной конструкции антенны является целесообразным.
СПИСОК ЛИТЕРАТУРЫ
1. Сомов А. М., Кабетов Р. В. Проектирование антенно-фидерных устройств. Учебное пособие для вузов / Под ред. Профессора А. М. Сомова. – М.: Горячая линия – Телеком, 2016. – 500с.: ил.
2. Юрцев О. А., Рунов А.В., Казарин А.Н. Спиральные антенны. – М.: Сов. Радио, 1974. – 224 с.
3. Айзенберг Г.З. и др. Антенны УКВ. Под ред. Г.З. Айзенберга. В 2-х ч.
Ч. 2. М., “Связь”, 1977 – 228 с.
4. Драбкин А. Л. и др., Д72 Антенно-фидерные устройства. Изд. 2-е, доп. «Сов. радио», 1974. 536 с. с ил.