Файл: Содержание Введение Определение пространственной ориентации объектов.docx

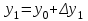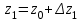, , , (2.1.2)

,
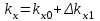уравнение (2.1.1) для момента времени t₁ можно представить в виде
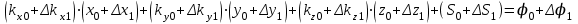(2.1.3)

или
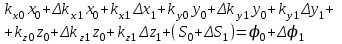. (2.1.4)
Вычитая (2.1.1) из (2.1.2), получим
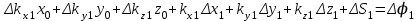. (2.1.4)
В результате получили систему уравнений относительно неизвестного начального положения вектора-базы x,y,z₀, приращения координат вектора-базы Dx,y,z₁, и приращения систематической погрешности DS. Если считать S постоянной величиной, то число неизвестных сократится до 6. Очевидно, что в данной системе уравнений достигается хорошая точность вычисления приращений координат вектора-базы, в то же время для получения достаточной точности начального положения необходимо некоторое время, пока приращения направляющих косинусов направлений на спутники достигнут достаточных значений.

Данную систему уравнений можно применять при постоянном созвездии навигационных спутников. Ее можно также использовать и при потере сигналов отдельных спутников, в этом случае число уравнений будет сокращаться.

При вводе в расчет новых спутников возникают проблемы, связанные с тем, что в качестве начального положения вектора-базы следует брать положение базы на момент ввода в расчет данного спутника. В результате для каждого спутника будет свое начальное положение вектора-базы, и из полученных уравнений нельзя будет составить систему.

Данную проблему можно решить следующим образом. Динамическая задача решается без добавления новых спутников, при этом потерянные спутники выводятся из расчета. Ввод в расчет новых спутников производится после полной инициализации системы уравнений. Следует отметить, что после инициализации падает точность вычисления начального положения вектора-базы. Для решения этой проблемы можно параллельно производить два аналогичных расчета, причем инициализацию производить поочередно через определенные интервалы времени.

Другой путь решения проблемы - составление рекуррентного алгоритма, в котором за начальное положение вектора-базы принимается текущее положение на предыдущем шаге.

---

Простейшим примером такого алгоритма является непосредственное решение системы уравнений (4), в которой все приращения вычисляются между предыдущим и текущим измерениями. В этом алгоритме будет всегда низкая точность вычисления начального положения, поскольку приращения направляющих косинусов направлений на НКА будет малым. Для осуществления фильтрации начального положения вектора-базы можно ввести в систему уравнений (4) априорные данные, полученные на предыдущем шаге:
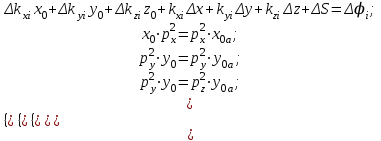(2.1.5)
где x_0a, y_0a, z_0a - априорное положение вектора-базы, полученные на предыдущем шаге:
x_0a = x₀ + Dx;_0a = y₀ + Dy (2.1.6)_0a = z₀ + Dz;

_x, p_y, p_z, - весовые коэффициенты, равные
,

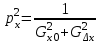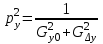(2.1.7)

,

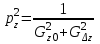G_x,y,z ,G_{Dx, Dy, Dz} - геометрические факторы (обусловленность системы уравнений) по соответствующим параметрам.
2.2 Динамический метод, использующий движение объекта
Система уравнений с учетом динамики объекта в общем случае включает семь неизвестных: три составляющие начальных координат вектора-базы в момент времени t0, три составляющие приращений координат вектора-базы за время наблюдения Dt и величину длины базы В, для ее решения необходимо принять сигналы шести НКА.

Задаваясь априорными значениями начальных координат x0, y0, z0, можно вычислить приращения координат вектора-базы Dxj, Dyj, Dzj, за j-й интервал времени. В первом приближении величинами x0, y0, z0, можно пренебречь ввиду малости коэффициентов Dkxij, Dkyij, Dkzij. В дальнейшем, после определения начального положения вектора-базы, его можно использовать в качестве априорных данных. При таком упрощении имеем систему уравнений с тремя неизвестными.

При измерении за K временных интервалов можно составить следующие системы уравнений:

Для j-го временного интервала (j = 1,2,јK)
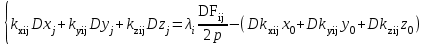(2.2.1)
Дополнительная система уравнений для всех интервалов
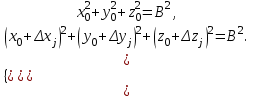(2.2.2)
Решая систему уравнений (2.2.2), можно с точностью 2-3 мм определить траекторию вектора-базы за любой интервал времени. Однако для определения ориентации знания траектории недостаточно, требуется знание начального положения вектора-базы x0, y0, z0. Полученные в результате решения системы уравнений (2.2.2) величины Dxj, Dyj, Dzj являются точками траектории вектора-базы за время наблюдения. Эти точки лежат на поверхности шара с радиусом, равным В, с центром в начале координат. Таким образом, задача определения начального положения вектора-базы сводится к определению параметров сферы возможных положений вектора-базы по заданной траектории, т.е. к задаче аппроксимации.

---

Начальное положение вектора-базы можно определить, решая систему уравнений. Раскрывая скобки, получим:
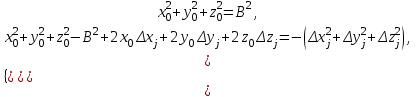(2.2.3)

или

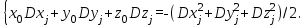(2.2.4)
Система (2.2.4) является линейной относительно неизвестных начальных координат базы x0, y0, z0.

Погрешность вычисления x0, y0, z0 зависит от величины приращений Dxj, Dyj, Dzj: чем больше по абсолютной величине приращения координат, тем выше точность вычисления начальных координат, при этом траектория вектора-базы не должна находиться в одной плоскости (в этом случае система уравнений (2.2.4)является вырожденной).

При известной величине базы систему уравнений (2.2.4) можно дополнить нелинейным уравнением из системы. В результате будем иметь следующую систему уравнений:
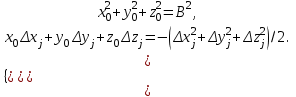(2.2.5)
Эта система уравнений остается невырожденной, даже если траектория вектора-базы будет лежать в одной плоскости.

Для решения системы уравнений (2.2.5) требуется поворот вектора-базы на достаточно большой угол.
2.3 Блок схема алгоритма


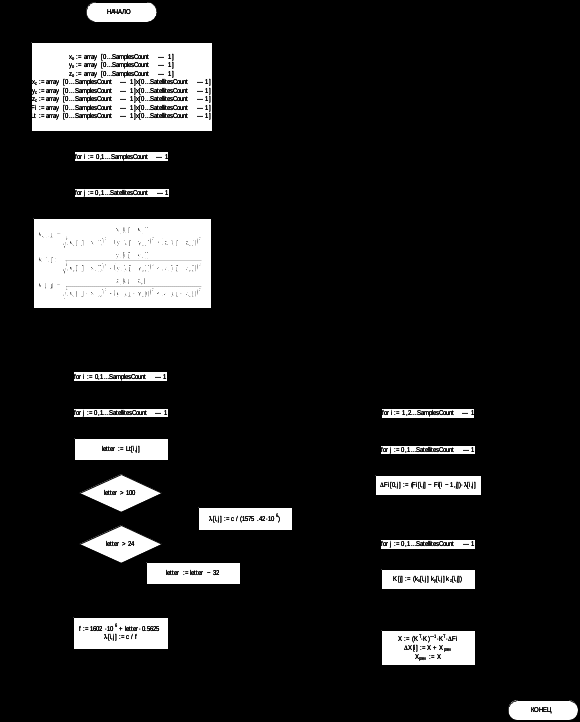
Рис. 2.3 Блок-схема динамического алгоритма определения угловой направленности вращающегося объекта
2.4 Моделирование алгоритма в MathCad
Для моделирования в MathCad14 файл формата *.xls с измерениями был разбит на 10 (Кс1, ……Кс10) файлов каждый из которых соответствует измерениям с одного спутника и содержит информацию о координатах НКА и измеренных фазах сигнала, также создан файл с координатами вектора базы.
.4.1 Получение исходных данных

---

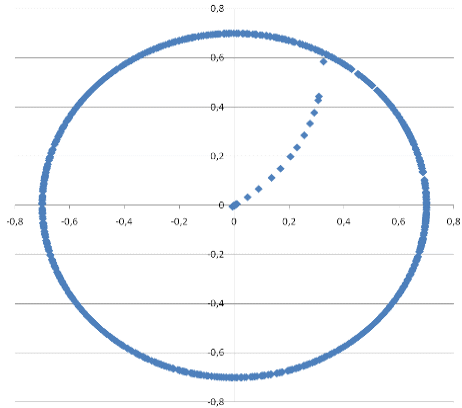
Рис. 2.4.1 результаты вычисления траектории вектора-базы (X, Z)


Рис. 2.4.2 результаты вычисления траектории вектора-базы (X, Y)

3 Экономическое обоснование работы

3.1 Экономический эффект от внедрения системы ГЛОНАСС
Принимая во внимание активное развитие спутниковых навигационных систем, в частности российской системы ГЛОНАСС, разработка приемоиндикатора является целесообразной.

При этом важно, чтобы приемоиндикатор был экономически эффективен и высокого качества. Качество зависит от функционально-технических характеристик, а его изменение оценивается индексом технического уровня разрабатываемой техники.

Для определения индекса технического уровня выберем:

• 
  ряд параметров отражающих уровень качества проектируемой техники;
  
• 
  аналог,который будет использоваться в качестве базы для сравнения.
  

Сравнение будем производить по ряду технических параметров: потребляемая мощность, надежность, масса и габариты изделия.

В качестве аналога возьмем ранее разработанный приемоиндикатор. При разработке основное внимание уделялось увеличению надежности устройства, уменьшению потребляемого схемой тока, уменьшению габаритных размеров.

Функционально-технические характеристики проектируемого устройства и его аналога, а также их численные значения и удельная значимость приведены в таблице 3.1.

Функционально-технические характеристики				Таблица 3.1
Функционально-технические характеристики	Единица измерения	Уровень функционально-технических характеристик			Значимость характерис- тики качества изделия (μi)
		Аналог А0	Проектируемый приемоиндикатор А1
Надежность		0,93	0,97		0,35
Вес	кг	1,60	1,45		0,15
Объем блока	дм3	1,95	1,78		0,15
Потребляемая мощность	Вт	20	13,5		0,35

---

Индекс технического уровня проектируемого приемоиндикатора определяется по формуле:

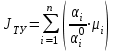(3.1)

где α_i, α_i⁰ – уровень i-й функционально-технической характеристики соответственно, проектируемого и базового изделий;

μ_i – значимость i-й функционально-технической характеристики качества изделия;

n – количество рассматриваемых функционально-технических характеристик.

Значимость i-й функционально-технической характеристики μ_i определяется экспертным путем, при этом .

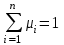Таким образом, технический уровень проектируемого изделия равен:



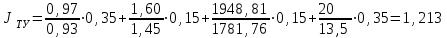
3.2 Определение показателей экономического обоснования проектируемого изделия

3.2.1 Затраты на проектирование и опытное производство проектируемого приемоиндикатора

Данные затраты определим по следующим статьям расходов:

• 
  основные материалы;
  
• 
  комплектующие изделия и покупные полуфабрикаты;
  
• 
  заработная плата разработчиков и рабочих, занятых при изготовлении опытного образца;
  
• 
  выплаты по единому социальному налогу;
  
• 
  прочие расходы.
  

Рассчитаем стоимость основных материалов. Будем считать, что для разработки и отладки нового изделия необходимо изготовить один опытный образец. Стоимость основных материалов приведена в таблице 3.2.

Стоимость основных материалов						Таблица 3.2
Наименование материала		Единица измерения		Расход на изделие	Цена за единицу, руб.		Сумма затрат, руб.
1		2		3	4		5
Проволока ММ-0,3 ТУ 16.к71-087-90		м		0,87	3,0		2,61
Трубка 3,31 ТВ-40-230,3 1 сорта ГОСТ 19034-82		м		0,16	5,0		0,8
Трубка 3,31 ТВ-40-230,6 1 сорта ГОСТ 19034-82		м		0,25	2,0		0,5
Трубка 3,31 ТВ-40-230,8 1 сорта ГОСТ 19034-82		кг		0,35	160		56
Нитки х/б 0 “особопрочные” глянцевые ГОСТ 6309-87		м		2,9	2,0		5,8
Спирт этиловый ГОСТ 17299-78	л		0,15		51	7,65
Лак АК-113 ГОСТ 23832-79	кг		0,05		63	3,15
Эмаль ЭП-51 черная, Т2 ГОСТ 9640-85	кг		0,06		42	2,52
Краска МКЭ ОСТ 107.9.4003-96	кг		0,02		40	0,8
Припой Прв КР2 ПОС-61 ГОСТ 21931-76	кг		0,81		180	145,8
Флюс ФКСп	кг		0,1		140	14
Мастика по ИЕ0.045.203	кг		0,01		44	0,44
Итого:	240,07

---