Файл: Решение 3 2 1 4 в соответствии с принципом суперпозиции магнитная индукция поля в в 1 в 2.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 326
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, где: 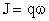 - амплитудное значение тока.
- амплитудное значение тока.
Круговую частоту w можно вычислить через период колебаний Т по формуле: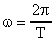 .
.
Учитывая формулу Томсона (9), окончательно получаем:
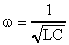 ;
; 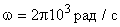 .
.
Отсюда: максимальная сила тока будет равна:
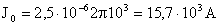 .
.
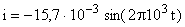 .
.
4) Определим максимальное значение объемной плотности энергии Wm магнитного поля катушки
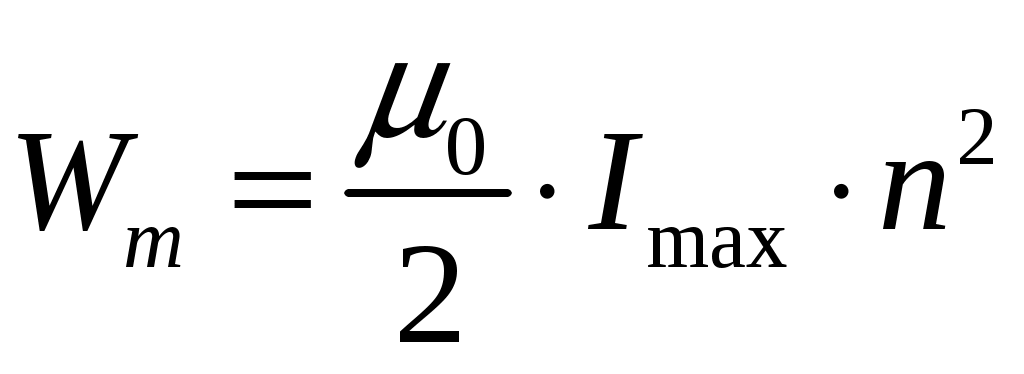 , где
, где  - число витков на единицу длины.
- число витков на единицу длины.
По закону сохранения энергии
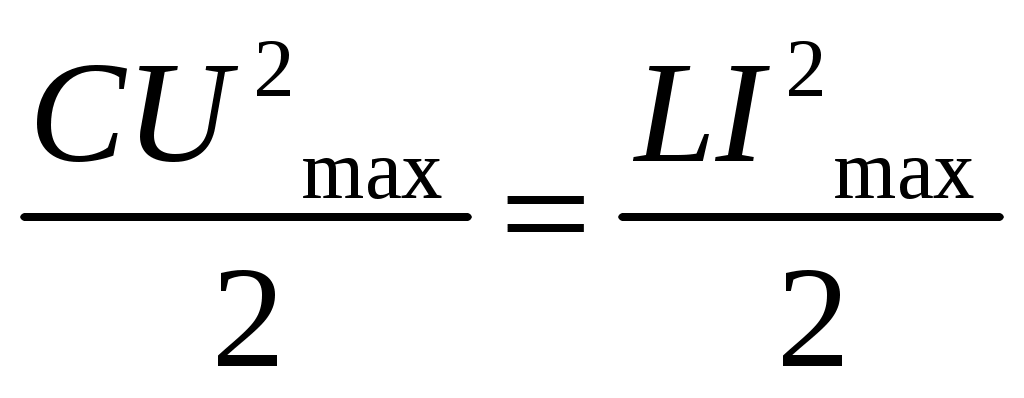 , отсюда
, отсюда 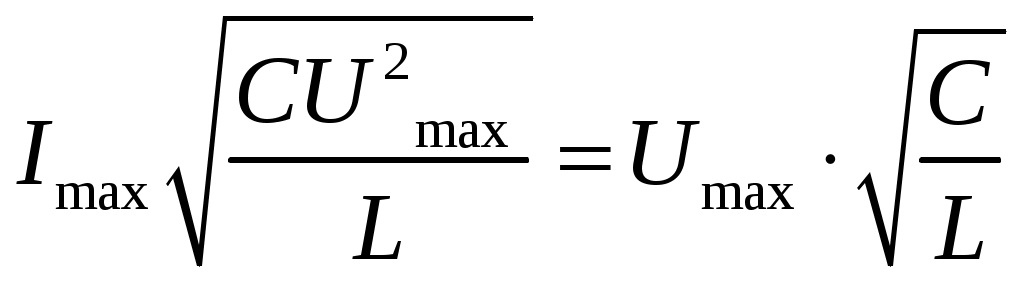 , тогда
, тогда
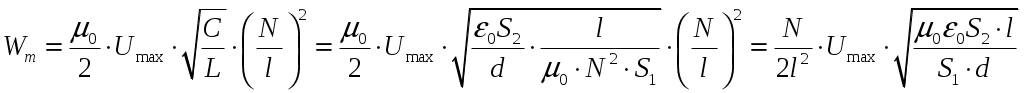 .
.
Подставляя данные, получим
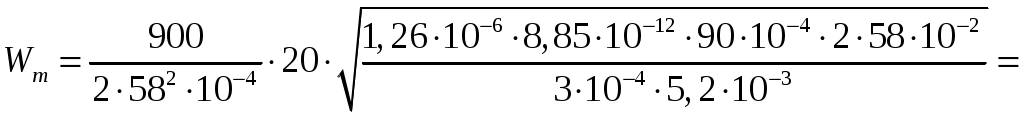
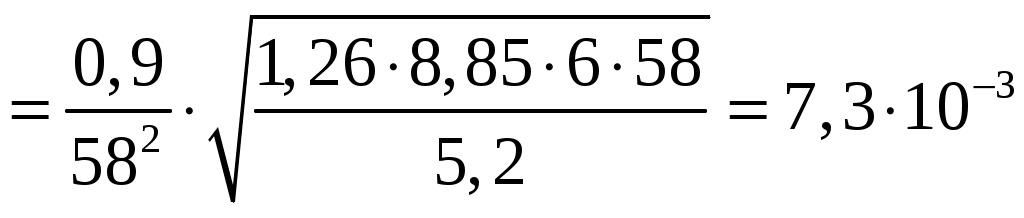 Дж = 7,3 мДж.
Дж = 7,3 мДж.
5) максимальное значение объемной плотности энергии We электрического поля конденсатора
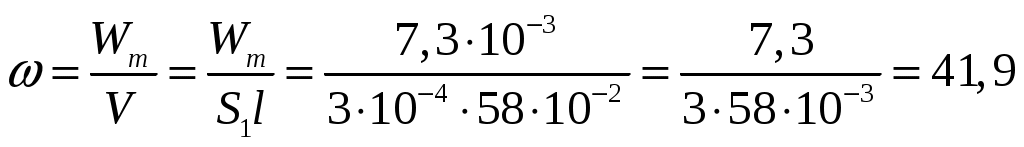 Дж/м3.
Дж/м3.
КОНТРОЛЬНАЯ РАБОТА 5.
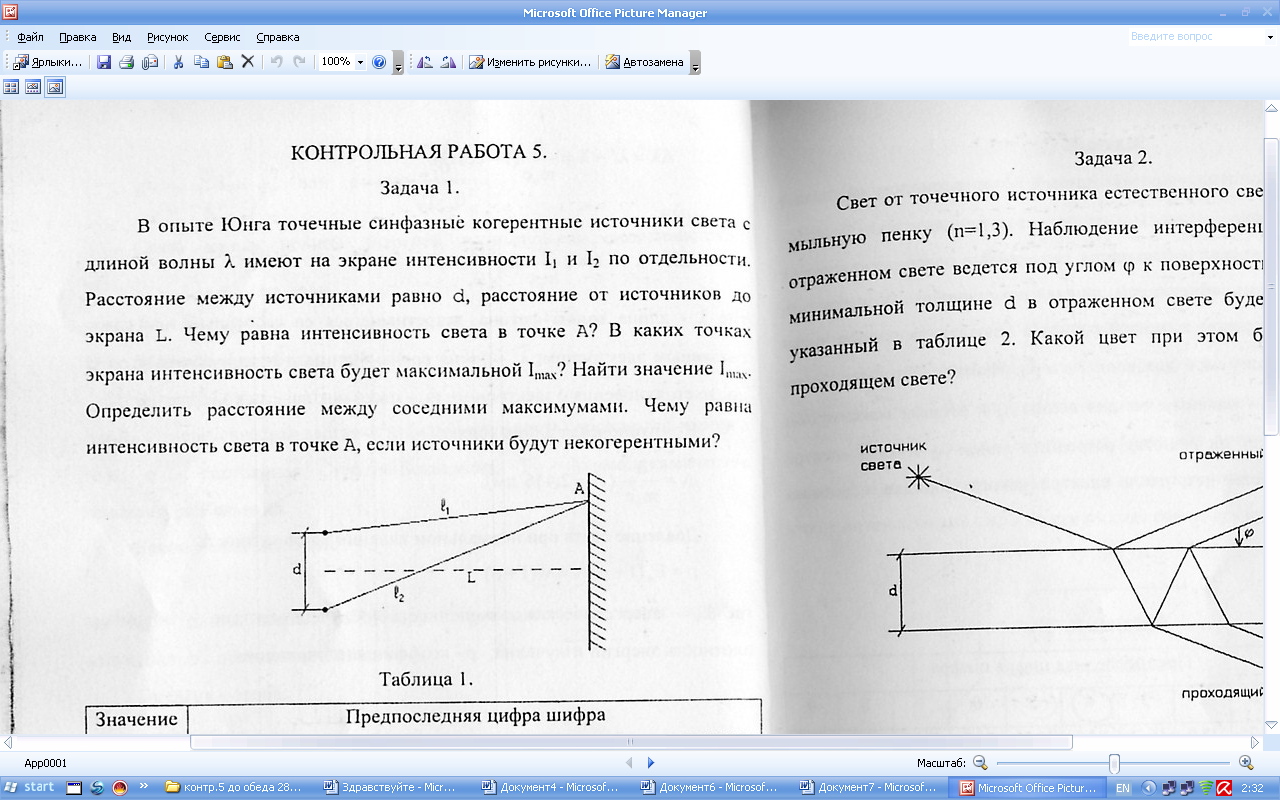
Задача 1.
В опыте Юнга точечные синфазные когерентные источники света с длиной волны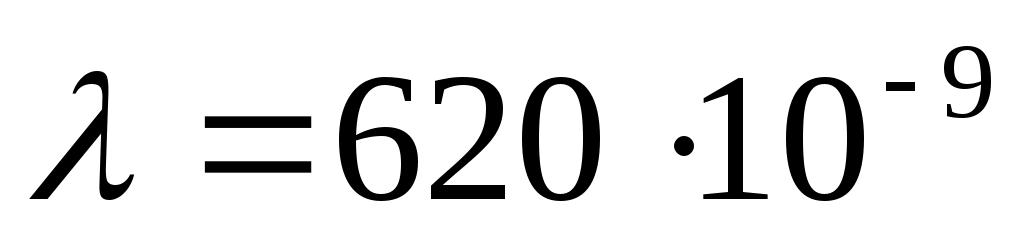 м имеют на экране интенсивности
м имеют на экране интенсивности 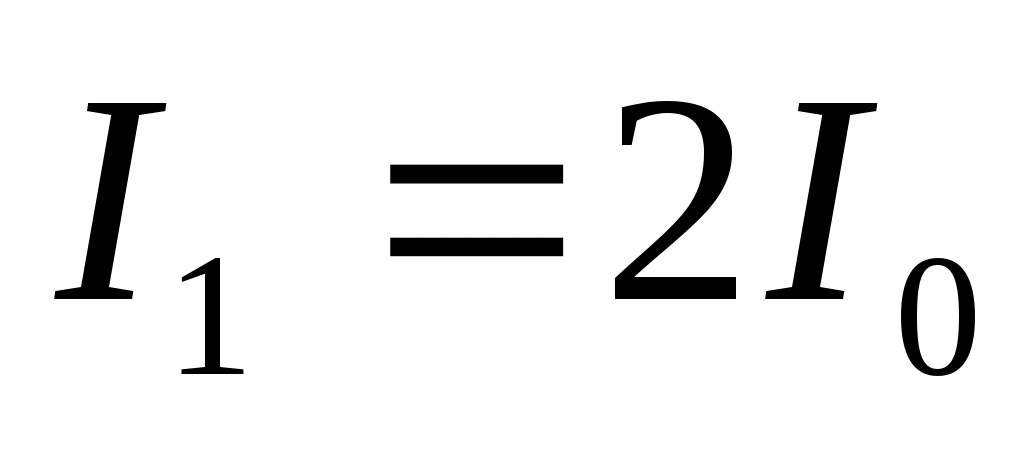 и
и 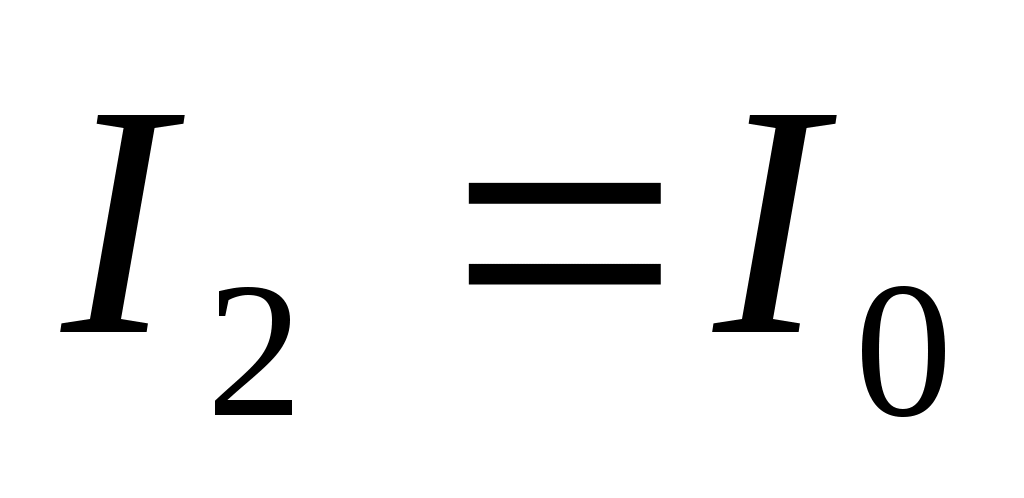 по отдельности. Расстояние между источниками равно d = 0,04 мм, расстояние от источников до экрана L = 3,2 м. Чему равна интенсивность света в точке А? В каких точках экрана интенсивность света будет максимальной
по отдельности. Расстояние между источниками равно d = 0,04 мм, расстояние от источников до экрана L = 3,2 м. Чему равна интенсивность света в точке А? В каких точках экрана интенсивность света будет максимальной 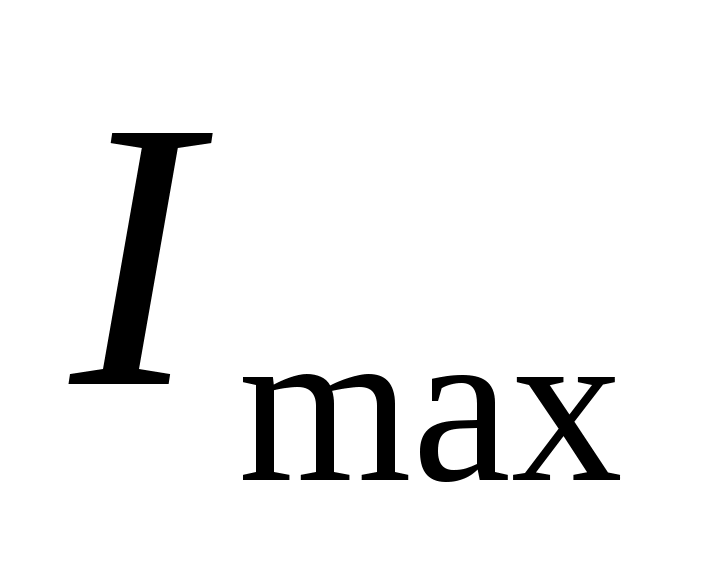
? Найти значение . Определить расстояние между соседними максимумами. Чему равна интенсивность света в точке А, если источники будут некогерентными?
. Определить расстояние между соседними максимумами. Чему равна интенсивность света в точке А, если источники будут некогерентными?
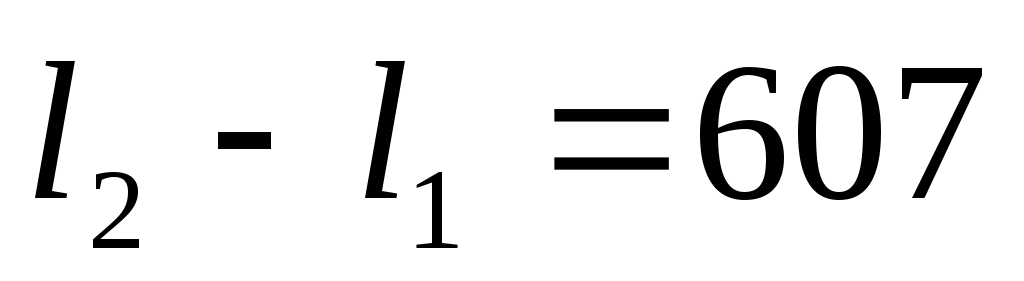
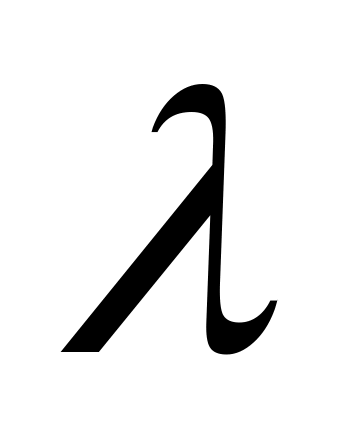
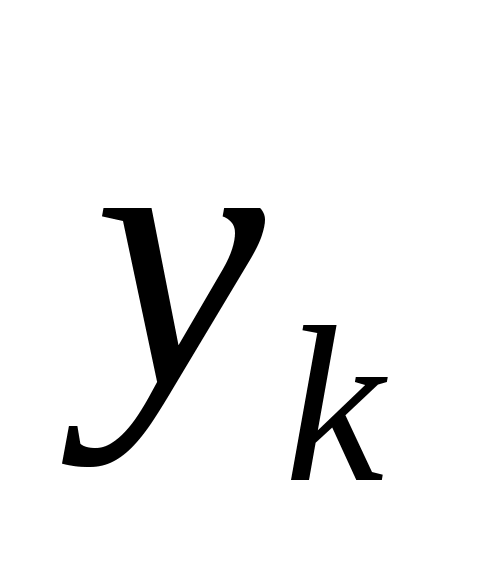
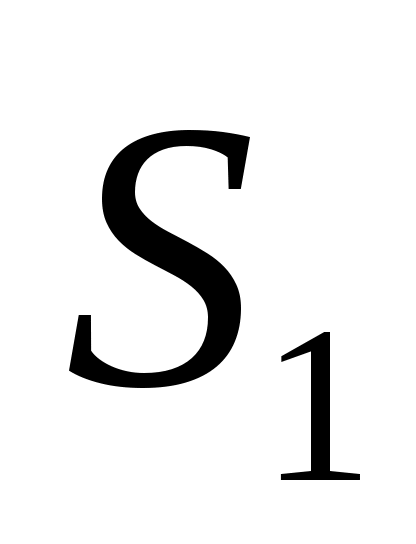
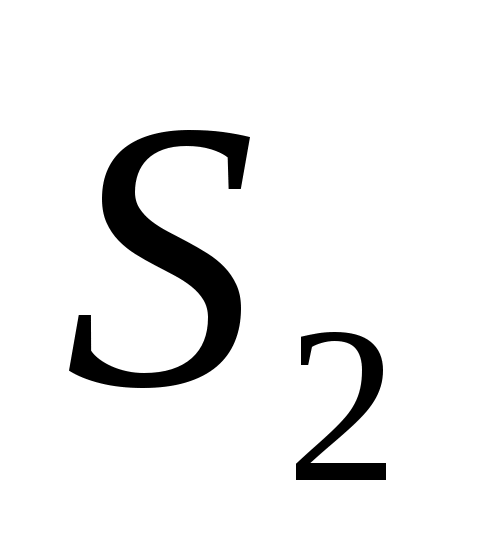


Решение:
1) интенсивность света в точке А
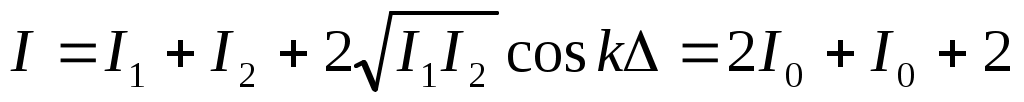
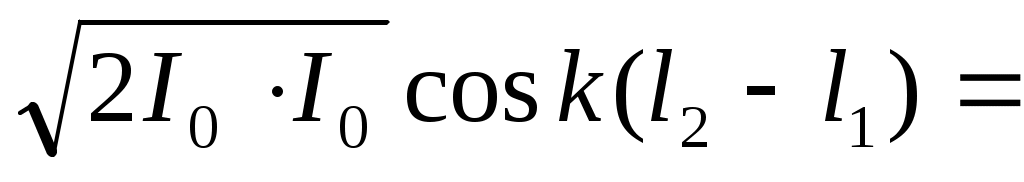
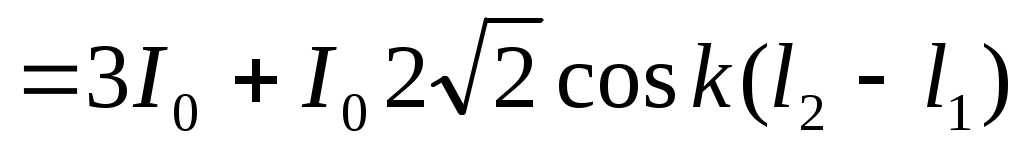
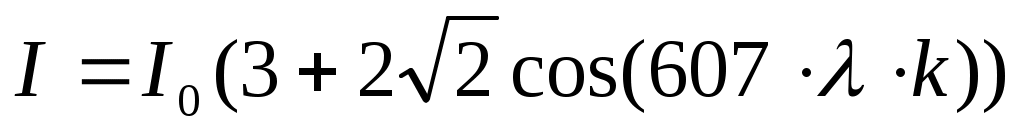
Где Δ=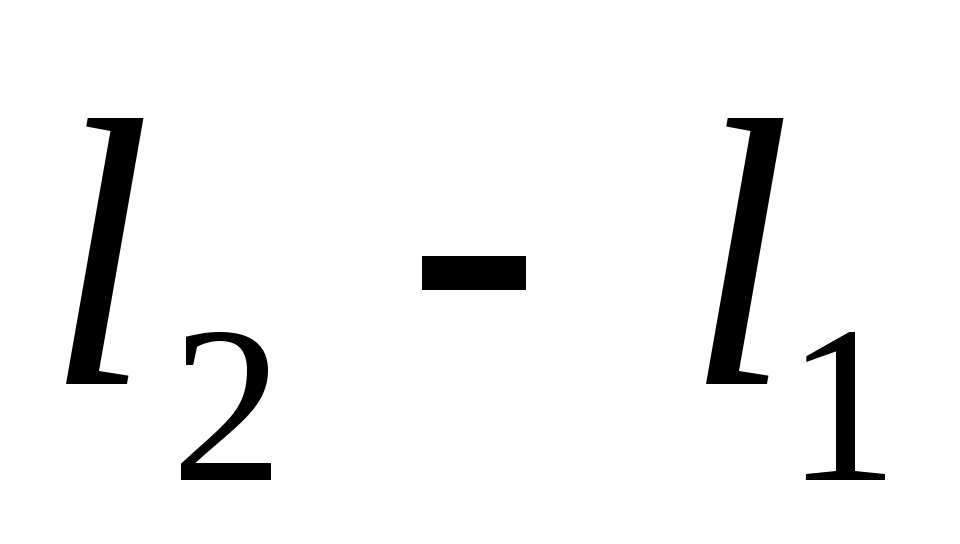 .
.
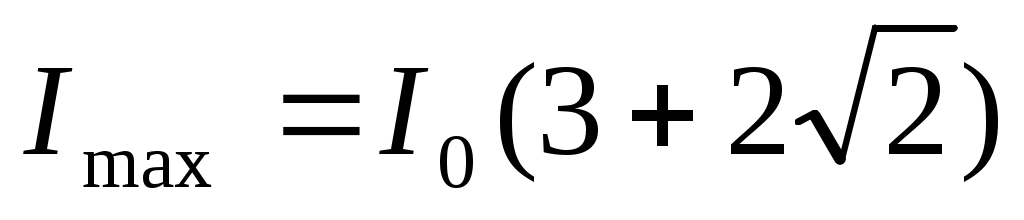 ,
, 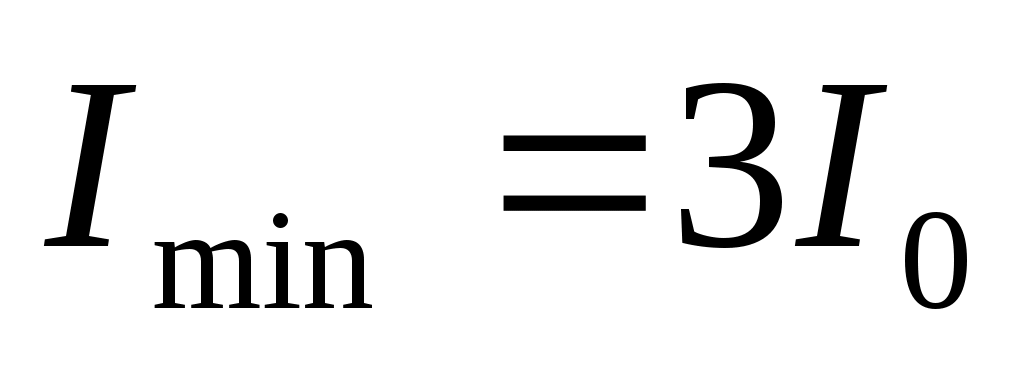 .
.
2) В точках интерференционных максимумов оптическая разность хода
Δ=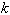 λ , где
λ , где 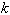 =0, 1, 2,... ;
=0, 1, 2,... ;
Условие интерференционных минимумов имеет вид:
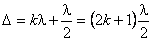 ;
;
Предположим, что в точке А находится k-й максимум на расстоянии ykот центральной полосы. Ему соответствует разность хода Δ=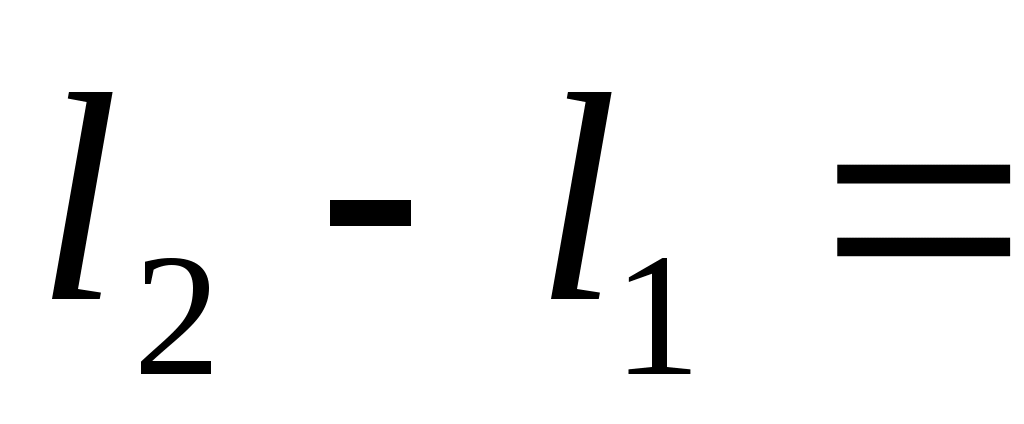 k λ .
k λ .
Из треугольника S1АC видно, что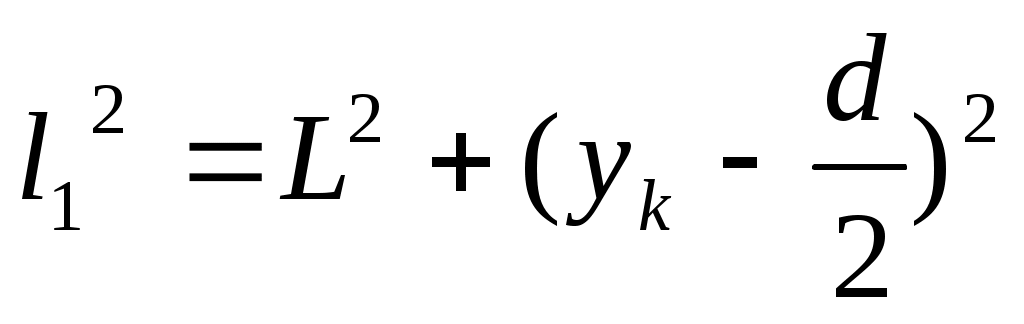 , а из треугольника S2АD видно, что
, а из треугольника S2АD видно, что 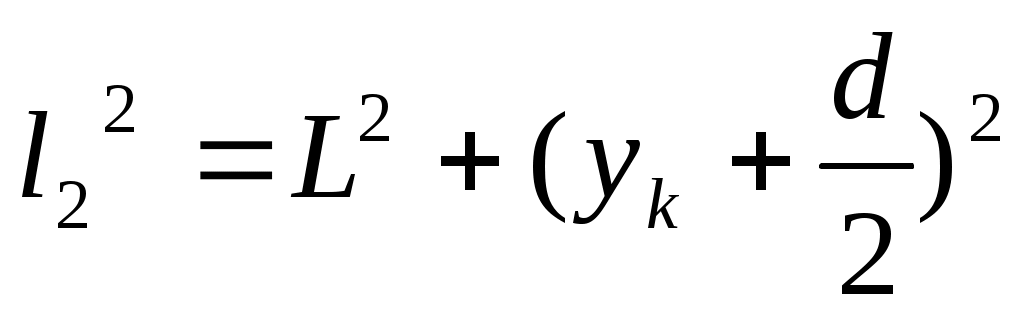 .
.
Из двух последних уравнений получим:
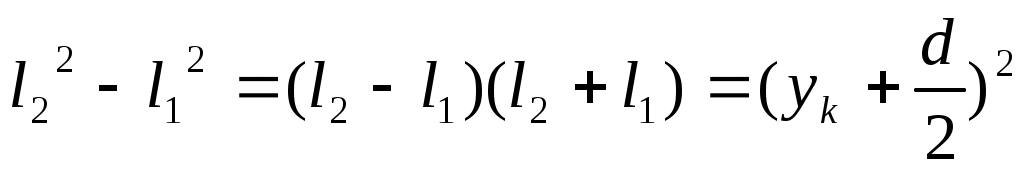
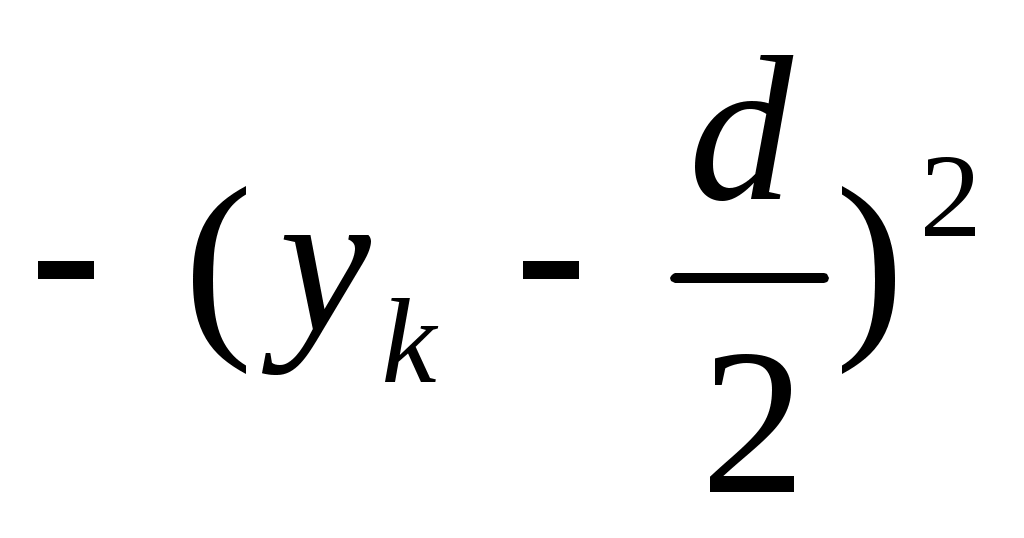 .
.
Учтём , что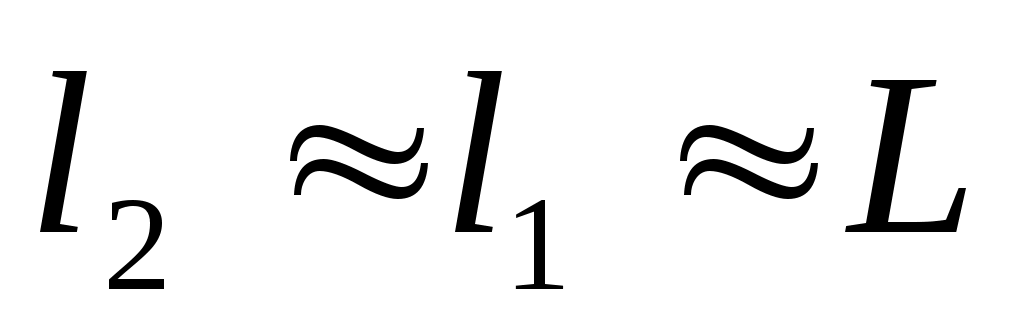 k λ;
k λ; 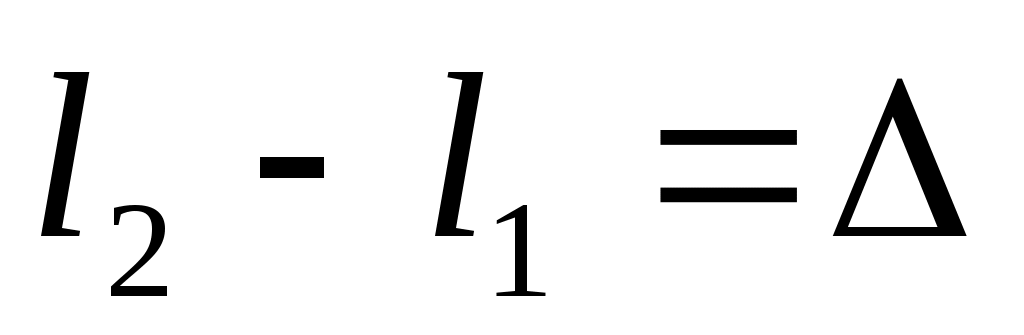 . Тогда
. Тогда 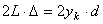 , откуда:
, откуда:
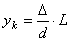 ;
;
Используя для максимумов условие Δ= λ , получим:
λ , получим:
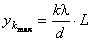 ;
;
где k = 1, 2, 3, … соответствуют интерференционным максимумам, расположенным выше точки А, а максимумам, расположенным ниже точки А, соответствуют k = -1, -2, -3, … Точке А соответствует центральный максимум (k = 0).
Используя условие интерференционных минимумов (2), можно найти их расстояния от центральной полосы по формуле (3):
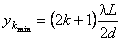 ;
;
Расстояние между соседними интерференционными максимумами (минимумами) называется шириной полосы и соответствует изменению k на единицу, то есть :
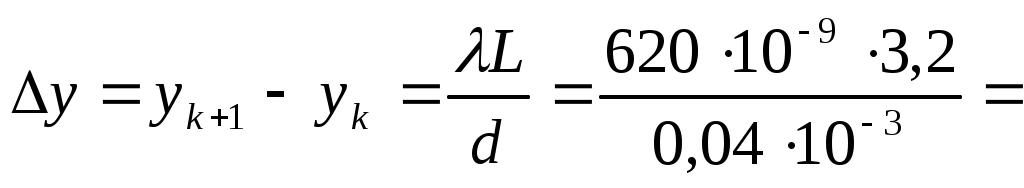
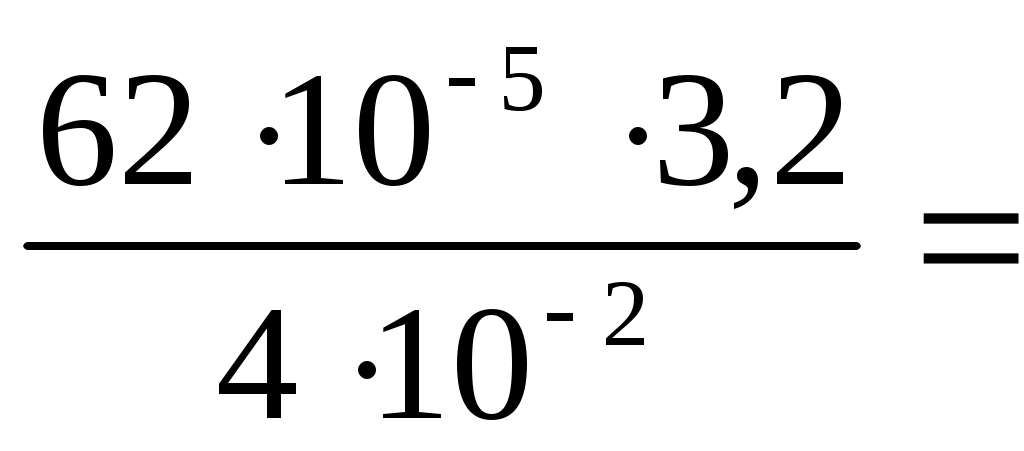
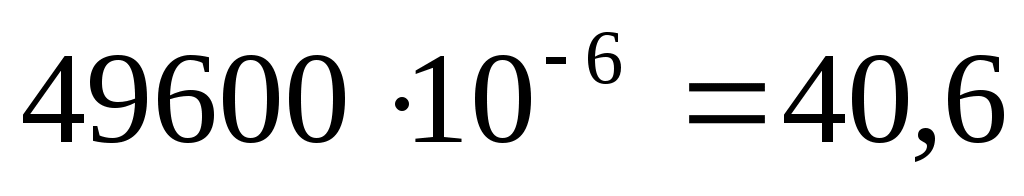 мм
мм
Ширина темных и светлых полос одинакова.
В опыте Юнга интерференционная картина представляет чередование интерференционных максимумов и минимумов в виде полос, параллельных щелям S1 и S2. В центре интерференционной картины расположена светлая полоса (k = 0). По обе стороны от центральной полосы расположены максимумы ±1, ±2, ±3, ±4 порядков интерференции. Разность хода между интерферирующими волнами по мере удаления от центральной полосы увеличивается. При этом по мере удаления от центра ухудшается видность и четкость интерференционной картины
, полосы размываются и исчезают, по условию последний максимум наблюдается при k = 4. Исчезновение полос означает, что колебания, пришедшие от двух источников S1 и S2, некогерентны. Пока их разность хода не превышала 4 λ, они были когерентны. Следовательно, максимальная разность хода, при которой наблюдается интерференция, будет равна:
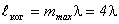
Величина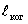 называется длиной когерентности. Если оптическая разность хода превышает длину когерентности, интерференционная картина не наблюдается.
называется длиной когерентности. Если оптическая разность хода превышает длину когерентности, интерференционная картина не наблюдается.
Задача 5.4
Между скрещенными поляризаторами света находится оптически активное вещество в виде пластинки длиной , постоянная вращения вещества равна . Вращение плоскости поляризации в веществе происходит по часовой стрелке в направлении распространения луча. Чему равна интенсивность света 2 на выходе второго поляризатора, если на первый поляризатор падает нормально естественный свет с интенсивностью о? Учесть дополнительное поглощение света в веществе, происходящее по закону Бугера (коэффициент поглощения равен ). На какой угол 2 и в каком направлении надо повернуть второй поляризатор, чтобы интенсивность света на его выходе равнялась нулю?
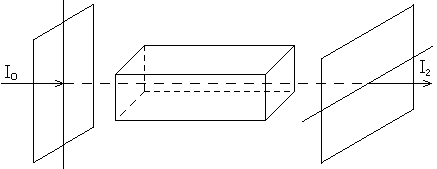
Решение
Интенсивность линейно поляризованного света, прошедшего через поляризатор, определяется законом Малюса
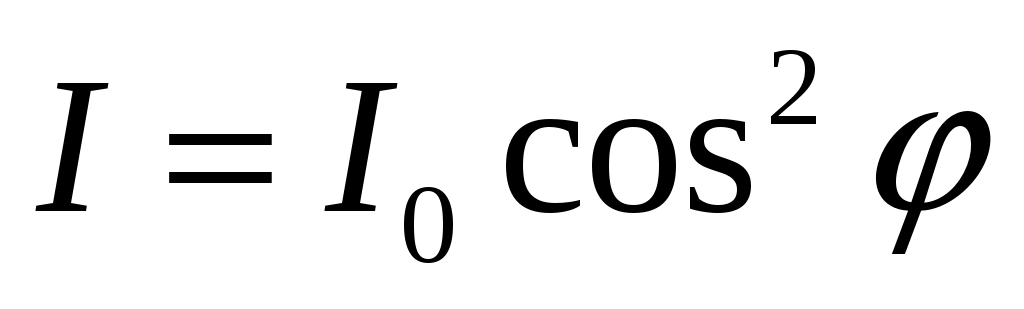 ,
,
где - угол между плоскостью поляризатора и направлением колебаний. Постоянная вращения вещества равна . Поэтому для определения надо взять значение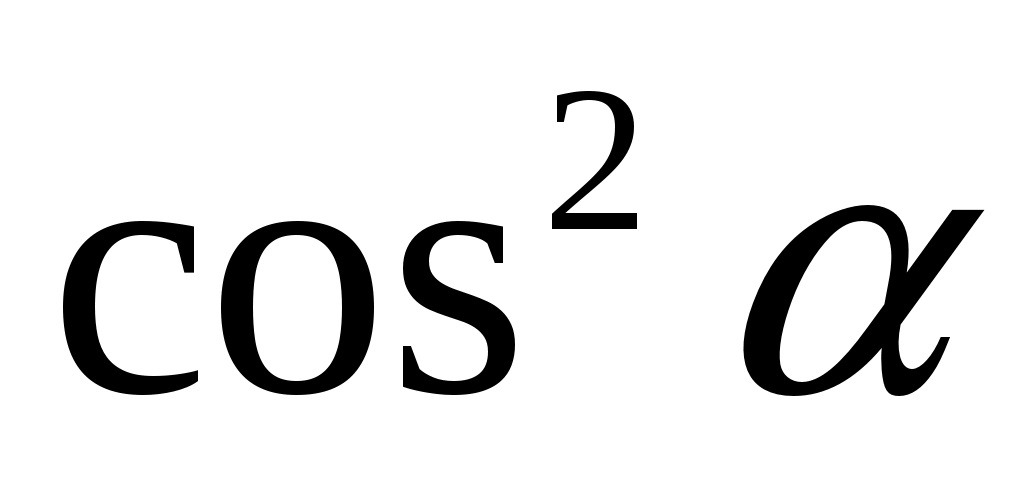 , которое, как известно, равно 1/2. Естественный свет на выходе из первого поляризатора будет линейно поляризованным с интенсивностью
, которое, как известно, равно 1/2. Естественный свет на выходе из первого поляризатора будет линейно поляризованным с интенсивностью 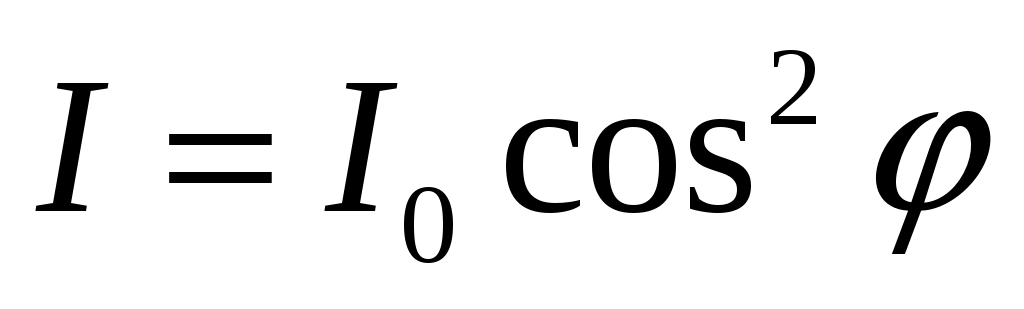 . Поле второго поляризатора интенсивность света будет:
. Поле второго поляризатора интенсивность света будет:
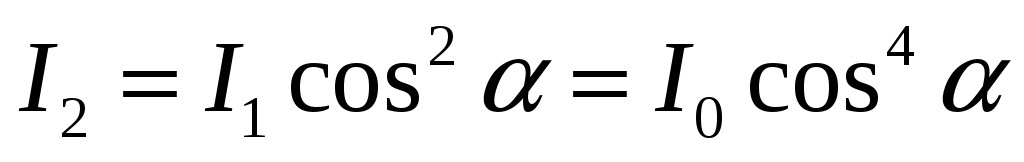 ,
,
Учитывая дополнительное поглощение света в веществе
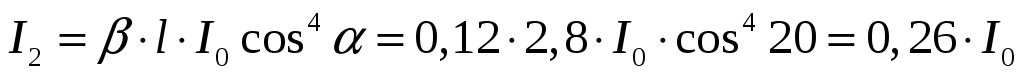
Вывод: интенсивность света 2 на выходе второго поляризатора составит 26% от первоначального, второй поляризатор надо повернуть на угол 90, чтобы интенсивность света на его выходе равнялась нулю.
Задача 5.
Степень черноты поверхности вещества рвана аТ = 0,65.Какая Энергия излучается с площади S = 60 см2 поверхности за время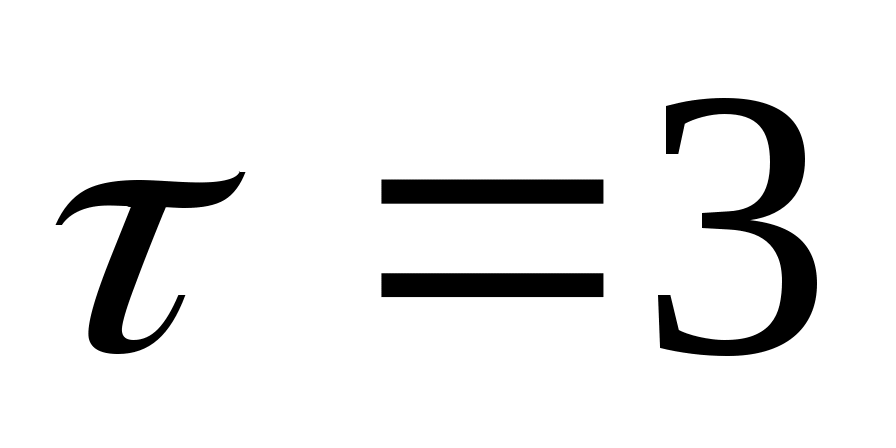 мин, если температура поверхности равна t = 900°С? Чему равна температура поверхности абсолютно черною тела такой же площади, излучающей за время
мин, если температура поверхности равна t = 900°С? Чему равна температура поверхности абсолютно черною тела такой же площади, излучающей за время  такую жеэнергию? На какую длину волны приходится максимум спектральной плотности энергетической светимости этого черного тела?
такую жеэнергию? На какую длину волны приходится максимум спектральной плотности энергетической светимости этого черного тела?
Решение:
1) Какая Энергия излучается с площади S = 60 см2 поверхности за время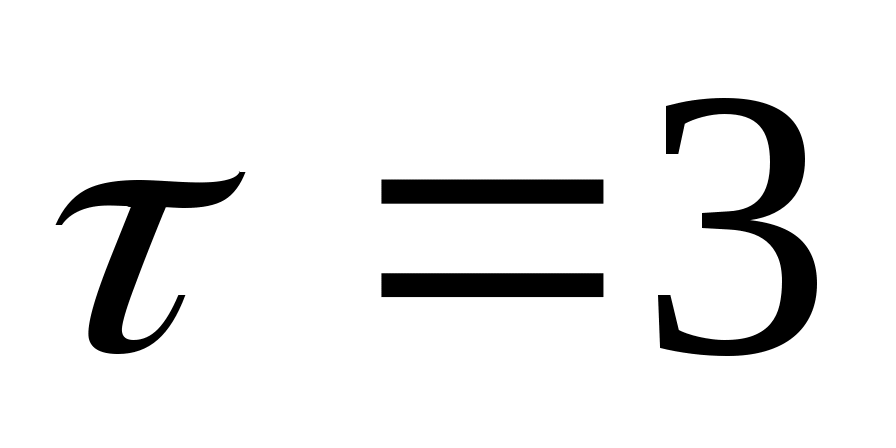 мин, если температура поверхности равна t = 900°С?
мин, если температура поверхности равна t = 900°С?
Энергетическая светимость (излучательность)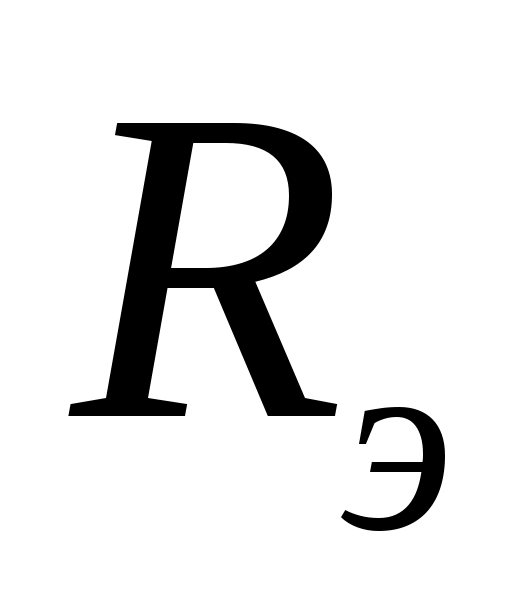 – это энергия W, излучаемая с единицы поверхности тела S за единицу времени t:
– это энергия W, излучаемая с единицы поверхности тела S за единицу времени t:
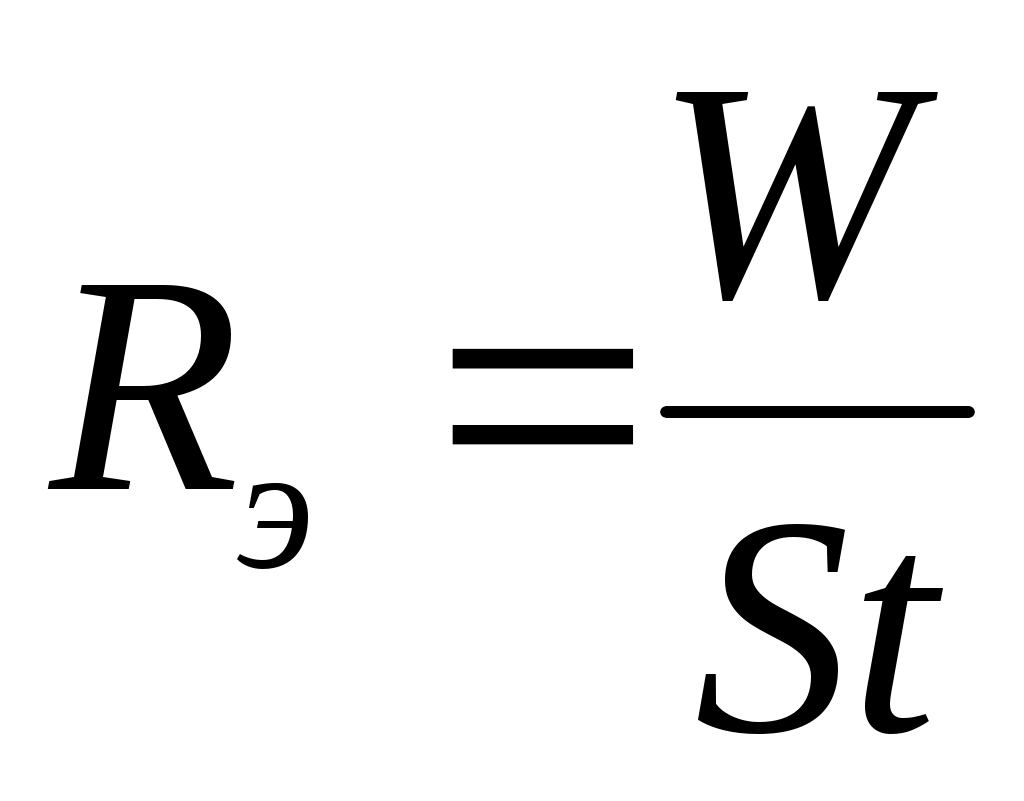 .
.
Энергетическая светимость (излучательность) абсолютно черного тела определяется формулой Стефана – Больцмана
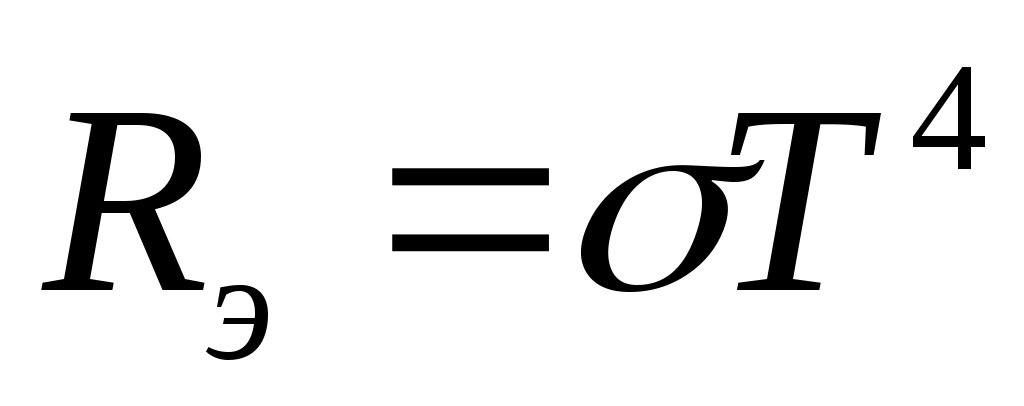 ,
,
где – постоянная Стефана – Больцмана, T– термодинамическая температура.
Круговую частоту w можно вычислить через период колебаний Т по формуле:
Учитывая формулу Томсона (9), окончательно получаем:
Отсюда: максимальная сила тока будет равна:
4) Определим максимальное значение объемной плотности энергии Wm магнитного поля катушки
По закону сохранения энергии
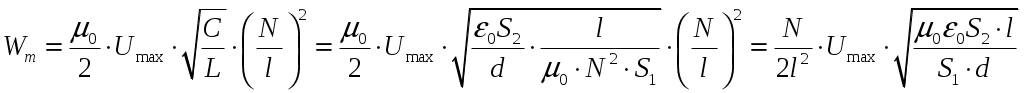 .
.Подставляя данные, получим
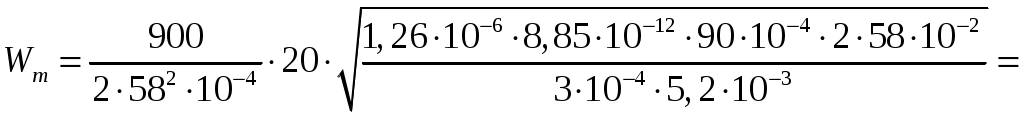
5) максимальное значение объемной плотности энергии We электрического поля конденсатора
КОНТРОЛЬНАЯ РАБОТА 5.
Задача 1.
В опыте Юнга точечные синфазные когерентные источники света с длиной волны
? Найти значение



Решение:
1) интенсивность света в точке А
Где Δ=
2) В точках интерференционных максимумов оптическая разность хода
Δ=
Условие интерференционных минимумов имеет вид:
Предположим, что в точке А находится k-й максимум на расстоянии ykот центральной полосы. Ему соответствует разность хода Δ=
Из треугольника S1АC видно, что
Из двух последних уравнений получим:
Учтём , что
Используя для максимумов условие Δ=
где k = 1, 2, 3, … соответствуют интерференционным максимумам, расположенным выше точки А, а максимумам, расположенным ниже точки А, соответствуют k = -1, -2, -3, … Точке А соответствует центральный максимум (k = 0).
Используя условие интерференционных минимумов (2), можно найти их расстояния от центральной полосы по формуле (3):
Расстояние между соседними интерференционными максимумами (минимумами) называется шириной полосы и соответствует изменению k на единицу, то есть :
Ширина темных и светлых полос одинакова.
В опыте Юнга интерференционная картина представляет чередование интерференционных максимумов и минимумов в виде полос, параллельных щелям S1 и S2. В центре интерференционной картины расположена светлая полоса (k = 0). По обе стороны от центральной полосы расположены максимумы ±1, ±2, ±3, ±4 порядков интерференции. Разность хода между интерферирующими волнами по мере удаления от центральной полосы увеличивается. При этом по мере удаления от центра ухудшается видность и четкость интерференционной картины
, полосы размываются и исчезают, по условию последний максимум наблюдается при k = 4. Исчезновение полос означает, что колебания, пришедшие от двух источников S1 и S2, некогерентны. Пока их разность хода не превышала 4 λ, они были когерентны. Следовательно, максимальная разность хода, при которой наблюдается интерференция, будет равна:
Величина
Задача 5.4
Между скрещенными поляризаторами света находится оптически активное вещество в виде пластинки длиной , постоянная вращения вещества равна . Вращение плоскости поляризации в веществе происходит по часовой стрелке в направлении распространения луча. Чему равна интенсивность света 2 на выходе второго поляризатора, если на первый поляризатор падает нормально естественный свет с интенсивностью о? Учесть дополнительное поглощение света в веществе, происходящее по закону Бугера (коэффициент поглощения равен ). На какой угол 2 и в каком направлении надо повернуть второй поляризатор, чтобы интенсивность света на его выходе равнялась нулю?

| Таблица 1. | |
| Значение | Предпоследняя цифра шифра |
| величин | 0 |
| (в | 20 |
| Таблица 2 | |
| Значение | Последняя цифра шифра |
| величин | 6 |
| (в мм) | 2.8 |
| (в | 0.12 |
Решение
Интенсивность линейно поляризованного света, прошедшего через поляризатор, определяется законом Малюса
где - угол между плоскостью поляризатора и направлением колебаний. Постоянная вращения вещества равна . Поэтому для определения надо взять значение
Учитывая дополнительное поглощение света в веществе
Вывод: интенсивность света 2 на выходе второго поляризатора составит 26% от первоначального, второй поляризатор надо повернуть на угол 90, чтобы интенсивность света на его выходе равнялась нулю.
Задача 5.
Степень черноты поверхности вещества рвана аТ = 0,65.Какая Энергия излучается с площади S = 60 см2 поверхности за время
Решение:
1) Какая Энергия излучается с площади S = 60 см2 поверхности за время
Энергетическая светимость (излучательность)
Энергетическая светимость (излучательность) абсолютно черного тела определяется формулой Стефана – Больцмана
где – постоянная Стефана – Больцмана, T– термодинамическая температура.