Вт/(м²·К⁴) — постоянная Стефана — Больцмана.

Для нечёрных тел можно приближённо записать:



где ε - степень черноты (для всех веществ ε < 1, для абсолютно черного тела ε = 1).

Тогда энергия излучается с площади S = 60 см² поверхности за время мин, если температура поверхности равна t = 900°С, будет равна

.

Произведем вычисления

Дж.

2) Чему равна температура поверхности абсолютно черною тела такой же площади, излучающей за время такую жеэнергию?

, отсюда



Тогда К = 780°С.

3) На какую длину волны приходится максимум спектральной плотности энергетической светимости этого черного тела?

Длина волны, при которой энергия излучения абсолютно чёрного тела максимальна, определяется законом смещения Вина:



где T — температура в кельвинах, а λ_max — длина волны с максимальной интенсивностью в метрах.

нм (в фиолетовой области спектра).

Задача 5.6

На поверхность металла падает монохроматическое излучение с длиной волны ₁ (значение работы выхода  приведено в таблице 1). Найти максимальную скорость v_max фотоэлектронов и задерживающую разность потенциалов U₃. Решить задачу для излучения с длиной волны ₂.

Таблица 1
Значение	Предпоследняя цифра шифра
величин	0
 (в эВ)	2.2

---

Таблица 2
Значение	Последняя цифра шифра
величин	6
1 (в 10-6м)	0.11
2 (в 10-12м)	2.0

Дано: A=2,2 эВ 1=0,1110-6м 2= 2.010-12м	Решение: 1) Формула Эйнштейна для фотоэффекта: , где h - постоянная Планка, ν - частота. По определению , с – скорость света.
Vmax = ? U3 = ?

Тогда .

Поэтому искомая скорость равна .

Подставляем числа:

Для ₁=0,1110^-6м



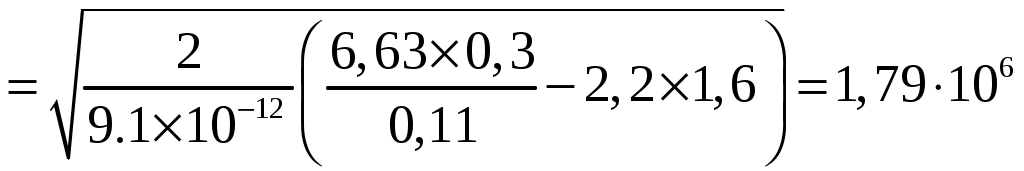м/с

Для ₂= 2.010^-12м



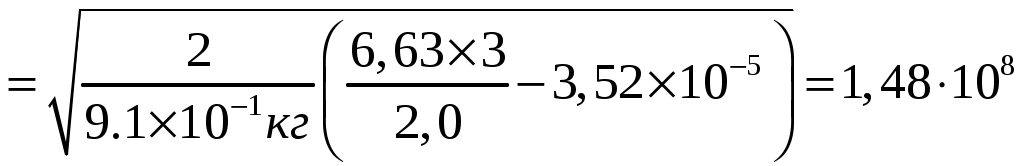м/с.
2) Формула Эйнштейна для фотоэффекта: . Если электрон задерживается обрат­ным потенциалом U (при этом прекращается фототок), то его максимальная кинетическая энергия, равная , должна быть меньше или равна потенциальной энергии электрона в потенциале: e×U. Поэтому

, поэтому .

Длина волны по определению равна: . Поэтому и

---

.

Подставляем числа:

Для ₁=0,1110^-6м



В.

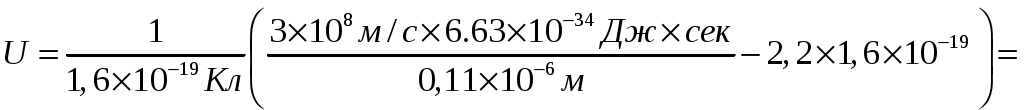
Для ₂= 2.010^-12м



В.

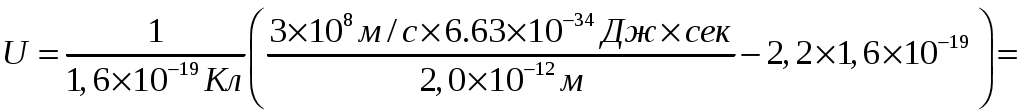
КОНТРОЛЬНАЯ РАБОТА 6.

Задача 6.1.

Электрон, находящийся на n-ой (n = 2) орбите атома водорода, поглощает фотон и переходит на орбиту номером т = 6. Определить:

1) массу поглощенного фотона

2) период обращения и кинетическую энергию электрона на m-ой орбите;

Энергия испускаемого фотона атомом водорода при переходе с орбиты номер n на орбиту с номером m определяется:



где - энергия ионизации атома водорода эВ.

Первая инфракрасная серия (серия Пашена) соответствует переходам электрона с орбиты номер n=4,5,6,… на орбиту номер m=3. Так, первая линия этой серии соответствует переходу электрона с орбиты номер n=4 на орбиту номер m=3. Четвертая линия в первой инфракрасной серии спектра атома водорода соответствует переходу электрона с орбиты номер n=7 на орбиту номер m=3.

Таким образом, энергия поглощения фотона равна:

эВ.

Полная энергия :



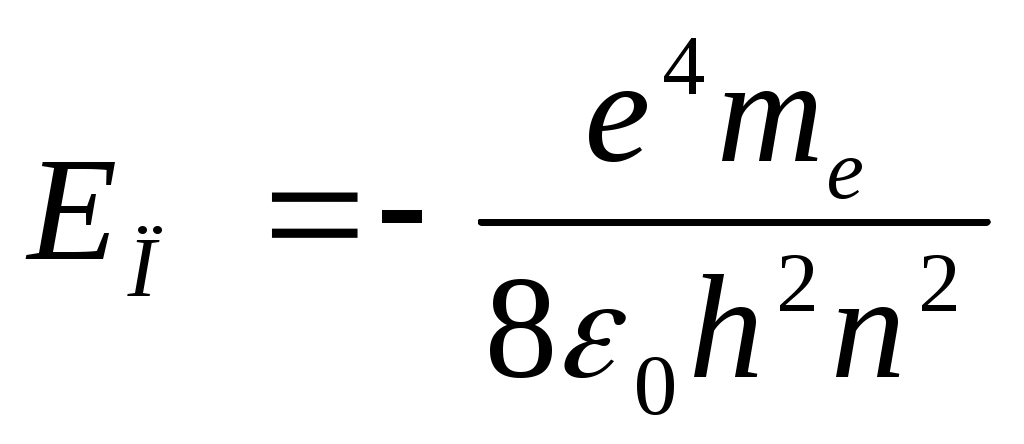
Подставляя значения m = 5 в формулу для полной энергии, получим:

Эв.

Кинетическая энергия :

Потенциальная энергия :

Из формул для кинетической и потенциальной энергий следует, что потенциальная энергия электрона в атоме водорода отрицательна по знаку и по модулю в 2 раза больше его кинетической энергии. Так как полная энергия есть сумма кинетической и потенциальной энергий, то легко получить, что

---

, Эв.

Кинетическая энергия выбиваемого электрона определяется разностью между энергией кванта излучения и энергией ионизации:



Отсюда Гц.
3) длину волны де Бройля для m-ой орбиты и ее с радиусом этой орбиты.

Длина волны де Бройля определяется формулой де Бройля:



где h = 6,62 · 10^-34 Дж · с – постоянная Планка; p – импульс электрона.

Импульс частицы можно определить, если известна его кинетическая энергия Е_КИН. Связь импульса с кинетической энергией различна для нерелятивистского случая (когда кинетическая энергия частицы много меньше ее энергии покоя) и для релятивистского случая (когда кинетическая энергия сравнима с энергией покоя частицы).

В нерелятивистском случае



где m₀ – масса покоя частицы (m₀ = 9,1 · 10^-31кг).

В нашем случае

м.
Задача 6.4

Точечный изотропный радиоактивный источник создает на расстоянии r в момент времени t₁ интенсивность излучения ₁, а в момент времени t₂- интенсивность ₂. Считая, что при каждом акте распада излучается один - квант с энергией , определить активности А₁ и А₂ в моменты времени t₁ и t₂. Определить период полураспада Т_1/2 и среднюю продолжительность жизни нуклида. Найти интенсивность излучения ₃ = 200 часов и первоначальное число не распавшихся атомов N_о.

Таблица 1
Значение	Последняя цифра шифра
величин	6
1(в мВт/м2)	2,2
t1(в час)	4
r (в м)	0,38
Таблица 2
Значение	Последняя цифра шифра
величин	6
2(в мВт/м2)	0,17
t2(в час)	60
(в Мэв)	1,34

---

Решение:

Площадь сферы радиусом r (по которой равномерно распределена интенсивность) S=4пr²

Мощность, выделяющаяся при распаде P=IS=4пr²I

Активность (количество распадов и выделяющихся квантов)
A=P/E=4пr²I/E
A₁=4п*(0,38 м)²*2,2*10^-3 Вт/м²/(1,34*10⁶ эВ*1,6*10^-19 Дж/эВ)=1,86*10¹⁰ с^-1

A₂=4п*(0,38 м)²*0,17*10^-3 Вт/м²/(1,34*10⁶ эВ*1,6*10^-19 Дж/эВ)=1,43*10⁹ с^-1

ln(A₂/A₁)=-λ(t₂-t₁)
постоянная распада λ=ln(A₁/A₂)/(t₂- t₁)=

=ln(1,86*10¹⁹/1,43*10¹⁸)/(56ч*3600с/ч)=1,27*10^-5 с^-1


период полураспада Т_1/2=ln2/λ=5,46*10⁴ c= 54578,52 c = 15,2 ч

средняя продолжительность жизни =1/λ=1/1,27*10⁵ c = 78740 c = 21,9 ч
число атомов N=N₀*e^-λt

при этом активность A=λ*N=λ*N₀*e^-λt

исходное число атомов

N₀=A*e^λt/λ=1,86*10¹⁰ с^-1*e^{0,00127 1/c*4ч*3600с/ч}/1,27*10^-5 с^-1=1,46*10¹⁵


Задача 6.5

Определить порядковый номер Z и массовое число A частицы обозначенной буквой X в символической записи ядерной реакции.



Решение:

Определить порядковый номер Z и массовое число A частицы обозначенной буквой X : .



Это будет бор.

Найти энергию ядерной реакции, освобождается или поглощается энергия?

Произведём расчёт энерговыделения при ядерной реакции:

= 7,01601 а.е.м. + 4,00260 а.е.м. –

– (10,01294 + 1,00867) а.е.м. = –0,003 а.е.м. = –0,00498 · 10^-27 кг
E = Δmc² = –0,00498 · 10^-27 · 2,99793² · 10¹⁶ = –0,447 · 10^–12 Дж ≈ –2,7 МэВ

Ответ: поглощается энергии E = –2,7 МэВ .
Список литературы

1. 
   Дмитриева В.Ф. Физика. М.: ВШ, 1993. 415 с.
   
2. 
   Савельев И.В. Курс общей физики. Т.1. Механика. Молекулярная физика. М.: Наука, 1982. 432 с.
   
3. 
   Зисман Г.А., Тодес О.М. Курс общей физики Т.1. Механика, молекулярная физика, колебания и волны. М.: Наука, 1969. 340 с.
   
4. 
   Фирганг Е.В. Руководство к решению задач по курсу общей физики. М.: ВШ, 1977. 351 с.
   
5. 
   Чертов А.Г., Воробьев А.А. Задачник по физике. М.: ВШ, 1988. 527 с.
   
6. 
   Касьянов В.А. Физика. 11 кл.: Учебн. для общеобразоват. учреждений. - 2-е изд., дополн. - М.: Дрофа, 2004. - С. 281-307.
   
7. 
   Элементарный учебник физики /Под ред акад. Г.С. Ландсберга. - Т. 3. - М.: Физматлит, 2000 и предшествующие издания.
   
8. 
   Бутиков Е.И., Кондратьев А.С. Физика. Т. 2. Электродинамика. Оптика. - М.: Физматлит: Лаборатория базовых знаний; СПб.: Невский диалект, 2001. - С. 276-291.
   
9. 
   Белолипецкий С.Н., Еркович О.С., Казаковцева В.А. и др. Задачник по физике. - М.: Физматлит, 2005. - С. 247-251.
   
10. 
    Буховцев Б.Б., Кривченков В.Д., Мякишев Г.Я., Сараева И.М. Задачи по элементарной физике. - М.: Физматлит, 2000 и предшествующие издания.
    

---

Смотрите также файлы

• История развития финансовой системы России.docx

• Отчет по лабораторной работе 1 По дисциплине Компьютерная графика.docx

• Сабаты таырыбы Жеіс мерекесі. Сабаты масаты.docx

• Доклад История вооруженных сил с древности, Великой Отечественной Войны.docx

• Практическая работа 2 Современное учебное занятие в условиях введения обновленных фгос ноо, фгос ооо. Анализ с позиции системнодеятельностного подхода видеофрагментов учебных занятий.docx