Решение

a) Построить статистический ряд распределения частот.

Подсчитаем объем, выборка из генеральной совокупности: n=10.

Подсчитаем количество данных:

«5» – 3

«10» – 2

«15» – 1

«20» – 4

Всего:10

Получили ряд: 3, 2, 1, 4

Запишем в таблицу:

xi	ni
5	3
10	2
15	1
20	4
∑	10

Построенный вариационный ряд также называют статистическим распределением выборки.

b) Построить полигон распределения.

Для построения полигона частот обозначим на оси абсцисс возможные значения признака, а на оси ординат соответствующие частоты и полученные точки соединим отрезками

4………………………………………………….

3…………………………………………….

2……………………………………………….

1……………………………………………………….




0 5 10 15 20
c) Вычислить выборочную среднюю, дисперсию, моду, медиану.

1) Найдём выборочную среднюю:

(5•3+10•2+15+20•4) : 10 = 13

Или так:

(20+20+5+10+10+15+20+5+5+20) : 10 = 13.

2) Найдём дисперсию:

Для этого Сумму всех x_i надо разделить на n^

(5+10+15+20):4 = 12,5

3) Найдём моду:

Мода М₀ дискретного вариационного ряда – это варианта с максимальной частотой. В данном случае М₀ = 20. Моду легко отыскать по таблице, и ещё легче на полигоне частот – это абсцисса самой высокой точки: М₀ = 20.

4) Найдём медиану:

Медиана вариационного ряда – это значение, которая делит его на две равные части (по количеству вариант). Медиана считается так: если совокупность содержит чётное количество чисел, например, у нас 10, то 10:2 = 5,

---

m_e= 5
d) Построить выборочную функцию распределения.

Из таблицы n= 20+20+5+10+10+15+20+5+5+20=130

F₁₃₀ (x 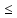1) = 0:130 = 0

F₁₃₀ (1
F₁₃₀ (2
F₁₃₀ (3
F₁₃₀ (4
F₁₃₀ (5
F₁₃₀ (6
F₁₃₀ (7
F₁₃₀ (8
F₁₃₀ (9
F₁₃₀ (x>10) = (0+20+20+5+10+10+15+20+5+5+20) :130 =1

Эмпирическая функция распределения имеет вид:

0, при x 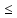1

0,153, при 1
0,3077, при 2
0,3462, при 3
0,4231, при 4
Fn (x) = 0,5, при 5
0,6154, при 6
0,7692, при 7
0,8077, при 8
0,8462, при 9
1, при x>10

Построим график кусочно-постоянной эмпирической функции распределения

1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0	1	2	3	4	5	6	7	8	9	10

---

Задание 4 (максимальное количество баллов - 4 балла)

Решите примеры, связанные с погрешностями, подробно описывая ход решения.

a) Округлить число 4,45575250 до шести, пяти, четырех, трех, двух и одного десятичных знаков; до целого числа.

4,45575250≈4,455753

4,45575250≈4,45575

4,45575250≈4,4558

4,45575250≈4,456

4,45575250≈4,46

4,45575250≈4,5

4,45575250≈4
b) Число 12,75 определено с относительной погрешностью 0,3%. Найдите абсолютную погрешность округления.

Относительная погрешность равна:

δ=(∆х : 12,75)⋅100%=0,3%.

Найдём абсолютную погрешность:

∆х : 12,75 = 0,3% : 100%;

∆х : 12,75 =0,003;

∆х =0,003 •12,75;

∆х =0, 0383.

c) Определите верные и сомнительные цифры числа 13,27 ± 0,03.

Цифра называется верной, если граница абсолютной погрешности данного приближенного значения числа не больше единицы того разряда, в котором записана эта цифра. В противном случае цифра называется сомнительной."

х= 13,27 ± 0,03

0,03- граница абсолютной погрешности

Единица последнего разряда - 0,01 (сотые)

0,03 > 0,01

значит цифра 7 - сомнительная

Далее :

0,03 < 0,1 -значит цифра 2 - верная
Задание 5 (максимальное количество баллов – 3 балла)

Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением.

На стороне AC треугольника ABC отмечена точка D так, что AD=3см, DC=10см. Площадь треугольника ABC равна 39 см². Найдите площадь треугольника ABD.

B А D H C

Дано: ∆АВС, AD=3см, DC=10см, SАВC = 39 см2. Найти: SАВD

Решение

ВН – общая высота треугольников.

S_АВC : S_АВD = АС : АD;

39 : S_АВD = 13 : 3;

S_АВD = 9 (см²)

Ответ. S_АВD = 9 (см²)
Задание 6 (максимальное количество баллов – 4 балла)

Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением.

---

Биссектриса угла A параллелограмма ABCD пересекает его сторону BC в точке F. Найдите площадь параллелограмма ABCD, если BF=4 см, FC=2 см, а угол ABC равен 150^°.

В 4 F 2 C 150° A D

Дано: ABCD – параллелограмм, BAF = FAD, BF=4 см, FC=2 см, ABC = 150°. Найти: SАВСD

Решение

1) BAF = FAD – по условию.

BFA = FAD – накрестлежащие при параллельных прямых АD || ВС, секущая АF.

Значит ∆ BAF – равнобедренный, и АВ = ВF = 4 см;

BFA = BAF = (180-150):2 = 15°

2) S_АВСD = 1/2•АВ•ВD•sinBAD;

S_АВСD =1/2• 4•6•1/2 = 6 (см²)

Ответ. 6 см².
Задание 7 (максимальное количество баллов – 3 балла)

Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением.

Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6см и 8см, а боковое ребро призмы равно 12см.

Дано: ABCDA1B1C1D1 – прямая призма, ABCD = A1B1C1D1 – ромбы, d1= 6 см, d2=8 см H = 12 cм. Найти: Sпр.

Решение.

S_пр. = 2 S_осн+ S_бок

1) S_осн = d₁•d₂;

S_осн = 6•8 = 24 (см²)

2) Диагонали ромба делят ромб на четыре равных, прямоугольных треугольника. Если длина диагоналей 6 и 8, то длина катетов треугольников соответственно 3 и 4, значит, длина гипотенузы или длина стороны ромба равна 5 (Пифагоров треугольник)

---

Значит длина стороны основания равна 5 см.

3) S_бок = Р_осн •Н

S_бок = 5•4•12 = 240 (см²)

4) S_пр. = 2 S_осн+ S_бок

S_пр. = 2•24+ 240 = 288 (см²)

Ответ. 288 см².

---

Смотрите также файлы

• Курсовая работа Исполнитель студент группы п21 С. В. Петров Научный.docx

• Кафедра Дошкольная педагогика, прикладная психология 44. 03.docx

• Как называется словарь русского языка, дающий возможность найти замену какомулибо слову или сочетанию, отвечающий на вопрос, как сказать иначе, как другими словами выразить ту же мысль, назвать тот или иной предмет.docx

• Авторские системы воспитания.docx

• Основные понятия курса анатомии центральной нервной системы.docx