Добавлен: 02.02.2019
Просмотров: 1700
Скачиваний: 31
1.Электрмагниттік әрекеттесу, оның сипаттамалары. Классикалық электрдинамиканың пәні және әдістері, басқа физика пәндері арасындағы орны.
Зарядталған бөлшектердің арасындағы өзара әрекеттесу электромагниттік әрекеттесу - деп аталады. Бұл процесс – электр заряды не магниттік моменті бар бөлшектер арасындағы электрмагниттік өріс арқылы берілетін өзара әсер. Электромагниттік өзара әсерлесудің де өзіндік әмбебап қасиеттері бар, олар өзара тартылыс (әр түрлі зарядтар арасында) және тебіліс (бірдей зарядтар арасында) қүбылыстары байқалады.
Әр түрлі зарядтардың әрекеттесу жағдайында тартылыс әсері, ал бірдей зарядтар әрекеттескенде тебілу әсері байқалады. Электромагниттік зарядтар қатысуымен болатын барлық процестерде заряд, импульс, энергия сақталу заңдары орындалады.
Электромагниттік байланыстың арқасында атомдар, молекулалар және макроскопиялық денелер пайда болады. Электр туралы ғылымның дамуының алғашқы кезеңінде бұл өзара әрекеттесудің электрлік және магниттік компоненттері бір-бірне байланыссыз түрде қарастырылды. Максвелл бұл екі күштің бір-бірімен тығыз байланысты екендігін дәлелдеді.
Ортаның
электрлік және магниттік қасиеттер
арасында келесі қатыс бар:
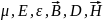 .
.
 Электромагниттік
өрісті сипаттайтын физикалық шамалар
арасында келесі қатыс бар:
Электромагниттік
өрісті сипаттайтын физикалық шамалар
арасында келесі қатыс бар:
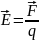 ,
,
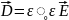 ,
,
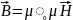 ,
,
![]() -
магнит тұрақтысы
-
магнит тұрақтысы
ɛ=1,
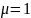
![]() ортаның магниттік өтімділігі
ортаның магниттік өтімділігі
Максвелл
теңдеулері электр және магнит өрістеріне
қатынасты симметриялы емес. Статционар
өріс үшін
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Классикалық электродинамика – макроскопиялық теорияларға жатады, қолданылу ауқымы үлкен болғанымен, шектелген; Яғни өрістің және зарядтардың дискретті сипаты құбылыстарға әсерін тигізбейтін кезде ғана электродинамика қорытындылары дұрыс болады. Теориялық физиканың маңызды бөлімі классикалық электродинамика мен арнаулы салыстырмалық теория болып табылады. Бұл мәселелер физика курсының бағдарламасында алатын орны үлкен. Сол себепті болашақ физика пәнінің оқытушысының бұл саладан білімі терең болуы тиіс. Сонымен бірге болашақ ғалым, инженер және техникалық қызметкер үшін де электродинамикадан білімі таяз болмағаны қажет. Осы тұрғыдан теориялық физика пәнінің оның ішінде классикалық электродинамиканың болашақ маман үшін маңызы жоғары.
2. Электр заряды. Заряд және ток тығыздығы. Зарядтың сақталу заңы. Вакуумдағы электрмагниттік өріс, оның зарядталған бөлшектерге әсері, өріс көздері.
Электр заряды – бөлшектер мен денелердің сыртқы электрмагниттік өріспен өзара әсерін, сондай-ақ олардың электрмагниттік өрістерінің өзара байланысын анықтайтын негізгі сипаттамалардың бірі. Э. з. 2 түрге ажыратылады және ол шартты түрде оң заряд және теріс заряд деп аталады. Э. з-ның бірліктердің халықаралық жүйесіндегі (СИ) өлшеу бірлігі – кулон (к).
Ток
тығыздығы-
ток бағытына перпендикуляр беттің
бірлік аудан арқылы өтетін ток күшімен
анықталады![]() Бұл
өрнектен
Бұл
өрнектен
![]() беттен
өтетін ток күші осы беттен өткен ток
тығыздығының векторының ағынына тең
екені шығады
беттен
өтетін ток күші осы беттен өткен ток
тығыздығының векторының ағынына тең
екені шығады
![]() Ток тығыздығын өткізгіштегі зарядтардың
реттелген қозғалысының
Ток тығыздығын өткізгіштегі зарядтардың
реттелген қозғалысының
![]() жылдамдығы,
ток тасмалдаушылардың
жылдамдығы,
ток тасмалдаушылардың
![]() концентрациясы
және тасымалдаушылардың
концентрациясы
және тасымалдаушылардың
![]() элементар
заряды арқылы төмендегідей өрнектеуге
болады
элементар
заряды арқылы төмендегідей өрнектеуге
болады![]()
Дененiң
электрлену кезiнде электр
зарядының сақталу заңы
орындалады: тұйық
жүйеде барлық бөлшектердiң зарядтарының
алгебралық қосындысы өзгерiссiз қалады.
Жүйе тұйық
деп аталады, егер зарядталған бөлшектер
одан сыртқа шықпаса және сырттан оған
енбесе.
![]() .
.
Зарядтың сақталу заңы бойынша зарядталған, бiр оң және бiр терiс зарядтардан тұратын, бөлшектер тек қосарланып қана пайда болады және жоғалады, мысалы, протон және антипротон, электрон және позитрон.
Электростатикалық өріс деп – қозғалмайтын электр зарядының өрісін айтады.
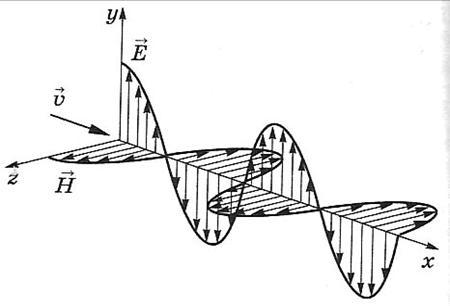
Оның вакуумдегі таралу жылдамдығы 300 000 км/с (жарықтың таралу жылдамдығымен бірдей). Біртекті изотроптық ортада электрлік кернеулік (Е) және магниттік кернеулік (Н) бірбіріне және толқынның таралу бағытына перпендикуляр болады, яғни электромагниттік толқын колденең толқын болып табылады. Кеңістіктің кез келген нүктесінде Е және Н толқындарының фазасы бірдей болады.
Вакуумдегі
электромагниттік өріс үшін мынадай
болып түрленеді:
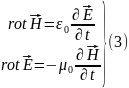
Теңдеулердің
бұл жазылымында электр және магнит
өрістерінің арасындағы байланыстар
ерекше айқын көрініп тұр. Олардың
біреуінің уақыт бойынша өзгерісі басқа
вектордың құйынды өрісін туғызады.
Айнымалы
электромагниттік өріс тербелістерінің
кеңістікте таралуын электромагниттік
толқын
деп атайды. Максвеллдің
болжамы бойынша электромагниттік
толқын тогы бар өткізгіштің бойымен,
диэлектрикте
және электр зарядтары жоқ вакуумде
де тарала алады. Максвелл теориясынан
шығатын аса маңызды салдардың бірі —
электромагниттік толқынның таралу
жылдамдығының шектілігі. Оның есептеулері
бойынша электромагниттік толқынның
таралу жылдамдығы:![]() м\с,
(3.1)
м\с,
(3.1)
мұндағы
![]() Ф\м
— электрлік және
Ф\м
— электрлік және
![]() Гн\м—
магниттік тұрақтылар. Бұл электромагниттік
өрістің іргелі қасиеті. Электромагниттік
толқынның ортадағы таралу жылдамдығы
Максвелл формуласы бойынша анықталады:
Гн\м—
магниттік тұрақтылар. Бұл электромагниттік
өрістің іргелі қасиеті. Электромагниттік
толқынның ортадағы таралу жылдамдығы
Максвелл формуласы бойынша анықталады:![]() ,
(3.2)
,
(3.2)
мұндағы
![]() —
ортаның сыну көрсеткіші,
—
ортаның сыну көрсеткіші,
![]() —
ортаның диэлектрлік және
—
ортаның диэлектрлік және
![]() —
магниттік өтімділіктері.
—
магниттік өтімділіктері.
Электромагниттік
толқынның теориялық есептеулер арқылы
табылған вакуумдегі жылдамдығы тікелей
өлшенген жарық жылдамдығына тең болуының
маңыздылығы ерекше
3.Электр және магнит өрістері. Электр өрісінің кернеулігі, магнит өрісінің индукциясы, суперпозиция принципі. Лоренц күші. Электрмагниттік өрістің электр және магнит өрістеріне жіктелуінің салыстырмалылығы. Е және В векторларын электрмагниттік өріс күйінің айнымалы сипаттамалары ретінде қарастыру.
Магнит өрісі
Электр зарядын қоршаған ортада электростатикалық өріс болатыны сияқты токтарды қоршаған ортада магнит өрісі болады. Магнит өрісі осы өріске әкелінген тоғы бар өткізгішке әсер ететін күш арқылы білінеді.
Токтардың магниттік өзара әсерлесуі материяның ерекше түрі – магнит өрісі - арқылы жүзеге асады. Магнит өрісінің негізгі қасиеті – сол өрісте орналасқан тогы бар өткізгішке күштің әсер етуі. Магнит өрісінің қасиеттерін зерттеу үшін тогы бар рамка қолданылады.
Берілген
нүктедегі магнит өрісінің бағыты
ретінде рамкаға жүргізілген
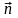 оң нормалінің өрістегі бағыты алынады.
Тогы бар рамкаға әсер ететін күштер
жұбының айналдыру моменті
оң нормалінің өрістегі бағыты алынады.
Тогы бар рамкаға әсер ететін күштер
жұбының айналдыру моменті
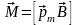 ,
,
мұндағы
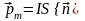 -
тогы бар рамканың магниттік моменті,
-
тогы бар рамканың магниттік моменті,
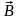 -
магнит индукциясының векторы деп
аталатын магнит өрісінің сандық
сипаттамасы.
-
магнит индукциясының векторы деп
аталатын магнит өрісінің сандық
сипаттамасы.
Магнит индукциясы векторының дивергенциясы әрқашан нольге тең, себебі табиғатта магнит зарядтары жоқ.
Біртекті магнит өрісінің берілген нүктесіндегі магнит индукциясы магниттік моменті бірге тең рамкаға, оған жүргізілген оң нормаль өріс бағытына перпендикуляр болғандағы, әсер ететін максималды айналдыру моменті арқылы анықталады.
Магнит индукцияның өлшем бірлігі - тесла (Тл).
Электр өрісінің кернеулігі деп өрістің берілген нүктесіндегі бірлік оң зарядқа әсер ететін күшпен анықталатын шаманы айтады.
Электростатикалық өрістің күштік сипаттамасы ретінде берілген нүктедегі электр өрісінің кернеулік векторы алынады:
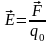 ,
(2.3) мұндағы
,
(2.3) мұндағы
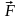 -
өрістің сол нүктесінде орналасқан
сыншы
-
өрістің сол нүктесінде орналасқан
сыншы
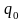 зарядқа әсер етуші күш..Вакуумдегі
нүктелік заряд өрісінің кернеулігі:
зарядқа әсер етуші күш..Вакуумдегі
нүктелік заряд өрісінің кернеулігі:
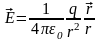 немесе
немесе
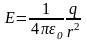 .
(2.4)
.
(2.4)
Электр өрісі кернеулігінің өлшем бірлігі – В/м.
Магнит
өрісінде
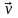 жылдамдықпен қозғалатын
жылдамдықпен қозғалатын
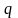 электр зарядына әсер етуші күшті Лоренц
күші
деп атайды:
электр зарядына әсер етуші күшті Лоренц
күші
деп атайды:
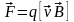 .
(24.2)
.
(24.2)
Лоренц
күшінің бағыты сол
қол ережесі
бойынша анықталады. Лоренц күшінің
модулі:
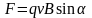 ,
мұндағы
,
мұндағы
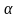 -
-
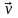 және
және
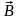 векторларының арасындағы бұрыш.
векторларының арасындағы бұрыш.
4. Кулон заңы және вакуумдағы электрстатиканың теңдеулері.
Кулон заңы — екі нүктелік электрикалық зарядтардың өзара әсерін сиппаттайтын заң.
Кулон заңы - тыныштықтағы екі нүктелік зарядтар зарядтардың модульдерінің көбейтіндісіне тура пропорционал, ара қашықтықтың квадратына кері пропорционал, таңбасы зарядтардың таңбаларының көбейтіндісімен бірдей, ал бағыты екі зарядты қосатын түзу бойымен бағыттас күшпен өзара әсер етеді
Векторлы түрде Ш. Кулон заңы тұжырымы былай жазылады:
![]()
мұндағы ![]() —
1 заряд 2 зарядқа әсер ететін күш;
—
1 заряд 2 зарядқа әсер ететін күш; ![]() —
зарядтар шамасы;
—
зарядтар шамасы; ![]() —
радиус-вектор (модулә
—
радиус-вектор (модулә ![]() -ге
тең 1 зарядтан 2 зарядқа бағытталған
вектор);
-ге
тең 1 зарядтан 2 зарядқа бағытталған
вектор); ![]() —
пропорционалдық коэффициенті. Осылайша,
заңға сәйкес біртекті зарядтар бір-бірін
итереді (ал әртекті — тартады).
—
пропорционалдық коэффициенті. Осылайша,
заңға сәйкес біртекті зарядтар бір-бірін
итереді (ал әртекті — тартады).
Электрстатикалық өріс теңдеулері
Кернеулік
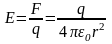
Суперпозиция
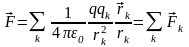
Потенциал
![]()
5. Био – Савар – Лаплас заңы және вакуумдағы стационарлық өрістің теңдеулері. Электрмагниттік индукция және Фарадей заңы.
Био-Савар
Лаплас заңы кез
келген бір тоғы бар өткізгіштін элемент
өрісінің бір нүктесіндегі магнит
өрісінің бағыты мен шамасын анықтайды,
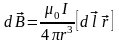
Модулі

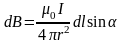 Би Савар Лаплас заның қарапайым жүйенің
магнит өрісін есептеу үшін қолдану .
1) Дөнгелек тоқтын центріндегі магнит
өрісін анықтау
Би Савар Лаплас заның қарапайым жүйенің
магнит өрісін есептеу үшін қолдану .
1) Дөнгелек тоқтын центріндегі магнит
өрісін анықтау
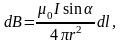
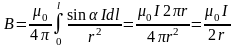 ,
,
2.
шексіз
түзу өткізгіштің бойымен өткен тоқтын
магнит өрісі
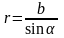 ,
,
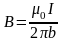
3.
үзын
соленойд немесе катушка ішіндегі магнит
индуқциясы
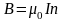 мұндағы n бірлік ұзындығына келетін
орам саны.
мұндағы n бірлік ұзындығына келетін
орам саны.
Магнит индукциясының күш сызықтары үшін,к.к нүктедегі жанамасы осы нүктедегі индукция вект.мен бағыттас сызық.н аламыз. Магнит инд.ң күш сызық.ң электр өрісінің кернеулік сызықтарынан ерекшеліг-ол әр уақытта тұйық болады.күш сызықтары тұйық болғандықтан оларды құйынды д.а.
Электромагниттік индукция құбылысы. Бұл құбылысты ағылшын физигі М.Фарадей 1831 жылы ашты.Бұл, тұйық өткізуші контурда, осы контур қамтитын, магниттік индукциялар ағынының өзгеруі кезінде, индукциялық атауын алған электр тогының туындауы болып табылады.
электромагниттік индукция құбылысының негізгі заңы немесе Фарадей заңы деп аталады, әрі бұл универсиалды заң.
Ei = -(dФ/dt) фарадей заңы
Φ = B · S · cos α магнит ағыны
6. Электр зарядының сақталу заңы және Максвеллдің ығысу тогы туралы гипотезасы
Электрстатикалық өріс
Электр зарядының сақталу заңы. Заттардын аса алуан түрлерінің болатындығына қарамастан,табиғатта электр зарядтарының 2 типі ғана өмір сүреді: былғарыға үйкелінген шыныда осындай пайда болатын заряд олады он деп аталады және теріге үйкелеген эбонитте осындай пайда болатын зарядтар теріс деп аталады. Бір атаулы зарядтар бір бірін тебеді ,әртүрлі атаулы зарядтар – бір бірін тартады.
Американдық
физик Р.Милликен тәжірбиелік электр
заряды
дискретті екенін
көрсетіп береді, яғни кез келген дененін
заряды е
элементар электр зарядынан бастап (е
= 1.6•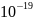 кл
кл
 тұтастай
еселік зарядтарды құрайды. Электрон
(
тұтастай
еселік зарядтарды құрайды. Электрон
(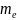 =
9.11
=
9.11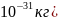 және
пратон
және
пратон
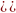 =1.67•
=1.67•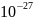 кг)
элементар теріс он зарядтардың
тасушылары болып саналады.
кг)
элементар теріс он зарядтардың
тасушылары болып саналады.
Электр заряды – релявистік инвариантты шама, яғни есептеу жүйесіне қатысты емес, сондықтан бұл заряд козғала ма немесе тыныштықтама, оған қатысты емес.
Дененін еркін зарядтарынын шоғырлануына қатысты өткізгіштерге,диэлектриктерге және шала өткізгіштерге бөлінеді.
Өткізгіштер –электр заряды онынбүкіл көлемі бойынша орын ауыстыра алатынг дене.Өткізгіштер 2 топка бөлінеді 1)бірінші түрдегі өткізгіштер(металдар) – ондағы зарядтарды тасымалдау химиялық түрлендірулермен қоса жүрмейді.2)екінші түрдегі өткізгіштер(мысалы, балқыған тұзда , қышқылдын ерітінділені) – ондағы зарядтарды тасымалдау химялық өзгерістерге әкеледі.
Диэлектриктер(мысалы, шыны , пластмасс) іс жүзіндегі еркін зарядтар жоқ денелер.
Шала өткізгіштер ( мысалы , германий , кремний ) өткізгіштер мен диэлектриктер арасындағы аралық жағдайды иеленеді.Дененлердін бөлінуі өте шартты болып саналады, бірақ ондағы еркін зарядтар концентрациясынын үлкен айырмашылығы олардың тәртәбәндегә аса зор үлкен сапалық айырмашылықпен байланысты , сондықтан денелер өткізгіштерге, диэлектриктриктерге және шала өткізгіштерге бөлінеді.Электр зарядының бірлігі кулон
Максвеллдің
ығысу тогы туралы гипотезасы.Максвелл
электр және магнит өрістері туралы
эксперименттік нәтижелерін қорыта
келе кез келген зарядтар мен токтар
жійесі туғызатын электромагниттік
өрістін біріңғай теориясын ашты.
Максвелл кез келген магнит өрісі өзін
қоршаған кеністікте контурда индукциялық
тоқтың тууына себепші болатын электр
өрісін қоздырады деген болжам айтты.
Магнит өрісі электр өрісін тудырады ,
ал оның циркуляцисы мынаған тен
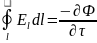 Мұндағы
Мұндағы
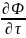 - магнит индукция ағынынын тек уакытка
ғана тәуелді екенін көрсететін
туынды.Егер тоқ жүретін контур және
магнит ағыны өтетін бет қозғалмайтын
болса , онда диференциялдау мен
интегралдау орындарын ауыстырып жазуға
болады
- магнит индукция ағынынын тек уакытка
ғана тәуелді екенін көрсететін
туынды.Егер тоқ жүретін контур және
магнит ағыны өтетін бет қозғалмайтын
болса , онда диференциялдау мен
интегралдау орындарын ауыстырып жазуға
болады
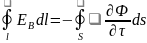 .
Электр өрісі кернеулік векторының
циркуляциясы кез келген тұйық контур
ішін нөолге тен болады
.
Электр өрісі кернеулік векторының
циркуляциясы кез келген тұйық контур
ішін нөолге тен болады
 алмастырып мынаны жазамыз
алмастырып мынаны жазамыз
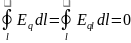 .Магнит өрісі электр тоғымен тығыз
байланысты болғандықтан айнымалы
электр өрісі қозлыратын магнит өрісін
Максвелл
ығысу тоғы
деп аталады .Ығысу тоғы пайда болу үшін
, Максвеллдін пікірінше текқана айнымалы
электр өрісінін болуы жеткілікті.Мұндай
құбылыс тізбектегі зарядталып және
разрядталып тұратын конденсатор
астарларынын арасында байкалады .
Конденсатор астарларынын арасы
өткізгішпен қосылмаған , айнымалы
электр өрісі арқылы ығысу тогы жүреді
.Магнит өрісі электр тоғымен тығыз
байланысты болғандықтан айнымалы
электр өрісі қозлыратын магнит өрісін
Максвелл
ығысу тоғы
деп аталады .Ығысу тоғы пайда болу үшін
, Максвеллдін пікірінше текқана айнымалы
электр өрісінін болуы жеткілікті.Мұндай
құбылыс тізбектегі зарядталып және
разрядталып тұратын конденсатор
астарларынын арасында байкалады .
Конденсатор астарларынын арасы
өткізгішпен қосылмаған , айнымалы
электр өрісі арқылы ығысу тогы жүреді
Электрстатикалық
өріс – электр
зарядын қоршаған кеністікке өзге заряд
енгізсек онда кулон күші әсер ететән
болады , демек хлектр зарядтарын қоршаған
кеністікке күш өрісі бар.Электростатикалық
өрісті аныктап тәжірибе дік зерттеу
үшін сынама нүктелік оң заряд
пайдаланылады. Егер Q заряды жасаитын
өріске сынама
зарядты орналастыратын болсақ онда
кулон занына сәйкес өрістін әртүрлі
зарядка F күші әскпр ететін
болады.Сондыктан
сынама
зарядты орналастыратын болсақ онда
кулон занына сәйкес өрістін әртүрлі
зарядка F күші әскпр ететін
болады.Сондыктан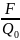 қатынасы
қатынасы
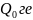 қатысты емес және сынама заряд бар
нүктедегі Электрстатикалық өрісті
сипаттаиды.
қатысты емес және сынама заряд бар
нүктедегі Электрстатикалық өрісті
сипаттаиды.
7. Вакуумдағы электрстатикалық өрістің теңдеулері. Электрстатикалық потенциал, оның қасиеттері, нормалау шарты. Нүктелік зарядтың потенциалы.
Вакуумдағы
электростатикалық өріс үшін гаусс
теоремасы.
Электростатикалық
өрістердің суперпозициялары принципінің
көмегімен электр зарядтары жүйесі
өрісінің кернеулігін есептеуді, еркін
тұйық бетке толассыз электр өрісінің
кернеулік векторының ағынын анықтауға
болады. Q нүктелік зарядын қамтитын, r
радиусын сфералық бетіне толассыз
кернеулік веторының ағыны: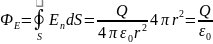
Бұл
формула еркін тұйықталған бетке
толассыз, вакуумдегі электростатикалық
өрістің кернеулік векторының ағыны,
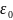 ге
бөлінген, зарядтардың осы бетінің
ішіндегі алгебралық қосындыға тең
ге
бөлінген, зарядтардың осы бетінің
ішіндегі алгебралық қосындыға тең
8. Пуассон теңдеуі және оның жалпы шешімі
Пуассон теңдеуі
![]()
-
— вещественная или комплексная функция
Үш еселі декарттық санақ жүйесіндегі теңдеу:
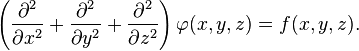
декарттық
санақ жүйесінде лаплас операторы ![]() түріне озгереді.Яғни,
түріне озгереді.Яғни,
![]()
![]() .
.
![]() —
электростатический потенциал,
—
электростатический потенциал,
![]() —зарядтың
көлемдік тығыздығы.
—зарядтың
көлемдік тығыздығы.
9. Электрстатикалық өрістегі өткізгіш. Шекаралық шарттар. Өткізгіш сыйымдылығы. Өткізгіштер жүйесі
Электростатикалық өрістегі өткізгіштер. Өткізгіште заряд тасушылар өте аз күштің әсерінен қозғала алады. Сондықтан өткізгіштегі зарядтардың тепе-теңдігі тек төмендегі шарттар орындалғанда ғана байқалады:
-
Өткізгіш ішінің барлық жеріндегі өріс кернеулігі нольге тең болуы керек:
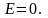
-
Өткізгіш бетінің әрбір нүктесіндегі өріс кернеулігі бетке нормаль бойымен бағытталған болуы керек:
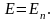
Демек, тепе-теңдік жағдайында өткізгіштің беті эквипотенциалды болады.
Егер өткізетін денеге аздаған q заряд берсек, онда ол тепе-теңдіктің шарттары орындалатындай болып таралады. Дене шегінде толық қамтылған кез келген тұйықталған бетті ойша елестетейік. Зарядтардың тепе-теңдік кезінде өткізгіш ішіндегі кез келген нүктеде өріс болмағандықтан, бет арқылы өтетін электрлік ығысу векторының ағыны нольге тең болады. Гаусс теоремасына сәйкес беттің ішіндегі зарядтардың алгебралық қосындысы да нольге тең болады. Бұл өткізгіштің ішінен қалауымызша жүргізілген кез келген өлшемдегі көлем үшін орынды. Демек, тепе-теңдік кезінде өткізгіштің ішіндегі ешбір жерде артық заряд болуы мүмкін емес, олардың барлығы өткізгіштің бетінде белгілі бір тығыздықпен орналасады.
Өткізгіштің (жеке оқшау өткізгіштің) электрлік сыйымдылығы – өткізгіштен шексіз қашықтықта орналасқан нүктенің электр потенциалы нөлге тең деп қабылданған және басқа барлық өткізгіштер шексіз қашықтықта орналасқан деп ұйғарған жағдайда (жеке оқшау өкізгіш деп аталады) өткізгіш зарядының (Q) оның электр потенциалы (U) қатынасына тең скаляр шама:
С = Q/U.
Жеке оқшау өткізгіш үшін электр сыйымдылық өткізгіштің өлшемдеріне, пішініне, сондай-ақ оқшаулаушы ортаның диэлектрикөтімділігіне (ɛr) тәуелді болады. Екі өткізгіш арасындағы электрлік сыйымдылық (екі өткізгіштің өзара электрлік сыйымдылығы) – өткізгіштер зарядтарының мәндері бірдей, ал таңбалары қарама-қарсы болған жағдайда және басқа барлық өткізгіштер шексіз қашықтықта орналасқан кезде өткізгіштің біріндегі зарядтың абсолюттік мәнінің осы екі өткізгіштің электр потенциалдары айырымыныңқатынасына тең скаляр шама:
С = Q/(ɸ1–ɸ2).
10. Диэлектриктің үйектелуі. Еркін және байланысқан зарядтар. Үйектелу векторы. Сегнетоэлектриктер.
Диэлектриктер - қалыпты жағдайда электр тогын өткізбейтін заттар. Классикалық тұрғыдан қарағанда диэлектриктер өткізгіштерден электр өрісі әсерінен реттелген қозғалыс жасап, электр тогын тудыратын еркін зарядтардың болмауымен ерекшеленеді. Диэлектриктердің атомдарындағы электрондар ядроларымен қатты байланысқан. Бұл байланысты бұзу үшін күшті сыртқы факторлар қажет.
Диэлектриктердің молекулалары электрлі нейтралды, ол қорытқы заряды нөлге тең жүйе сияқты. Осыған қарамастан молекулалардың электрлік қасиеті бар және ол молекулаларды электрлік диполь ретінде қарастыруға болады.
Мұндай
дипольдің оң заряды оң зарядтардың
«ауырлық центрінде» орналасқан ядроның
қорытқы зарядына тең, ал теріс заряды
теріс зарядтардың «ауырлық центрінде»
орналасқан электрондардың қорытқы
зарядына тең. Осындай дипольдің электрлік
моменті ![]() (
(![]() –
молекуладағы барлық атомдық ядролардағы
оң зарядтардың қорытқысы,
–
молекуладағы барлық атомдық ядролардағы
оң зарядтардың қорытқысы, ![]() –
электрондардың «ауырлық центрінен»
атомдық ядролардағы оң зарядтардың
«ауырлық центрін» қосатын вектор).
–
электрондардың «ауырлық центрінен»
атомдық ядролардағы оң зарядтардың
«ауырлық центрін» қосатын вектор).
Диэлектриктерді сыртқы электр өрісіне енгізілгенде сыртқы өріс әсерінен оларда нөлден өзгеше электр моменті пайда болады, яғни диэлектрик үйектелінеді (поляризацияланады).
Сыртқы электр өрісі әсерінен дипольдердің өріс бағытына сәйкес бағдарлану құбылысын диэлектриктердің үйектелуі деп атайды. Нәтижесінде диэлектриктің қандай да бір көлеміндегі электр моменті нолден өзгеше болады.
Диэлектриктер үш топқа бөлінеді: полярлы, полярлы емес және кристалды. Диэлектриктердің бұл үш тобы үйектелудің үш түрімен ерекшеленеді: полярлы емес диэлектриктерде электронды (деформациялы), полярлы диэлектриктерде бағдарланушы (дипольды), ионды кристалдық торлы диэлектриктерде ионды.
Сегнетоэлектриктер — белгілі температуралар аралығында (сегнетоэлектрлік фазаға сәйкес) бағыты сыртқы әсерлер арқылы (электр өрісімен немесе механикалық кернеулермен) өзгертіле алатын спонтанды поляризацияланған кристалл диэлектриктер (соның ішінде сұйық кристаллы).
Ерекшелігі[өңдеу] #
Сегнетоэлектриктерде бір жақты бағытталган спонтанды поляризация аймақтары — сегнетоэлектрлік домендер бар. Сыртқы әсерден Сегнетоэлектриктер көп домендікүйден монодоменді күйге өтуі мүмкін. Сегнетоэлектриктердің осы қасиеті ЕЭМ-ның еске сақтау құрылғыларын жасауда пайдаланылады. Көптеген Сегнетоэлектриктердің диэлектрлік өтімділігі және пьезоэлектрлік константаларының аномальды жоғары мәндері болады және cегнетоэлектриктердің физикалық қасиеттері температураға тәуелді.[1]
11 ,Диэлектриктегі скаляр потенциал. 10да жауабы
12.Электрстатикалық өрістің және зарядтардың өзараәрекеттесу энергиясы
Электромагниттік өріс энергиясының тербеліс жиілігіне тәуелділігі[өңдеу] #
Егер электр
заряды ![]() гармоникалық
заңдылық бойынша тербелсе, онда
оның үдеуі уақыт
бойынша
гармоникалық
заңдылық бойынша тербелсе, онда
оның үдеуі уақыт
бойынша ![]() гармоникалық
заңдылықпен өзгереді. Электромагнитті
толқынды үдемелі қозғалатын зарядталған
бөлшек шығарады. Олай болса,толқынның
электр өрісінің кернеулігі мен магнит
индукциясы үдеуге тура пропорционал. Электр
өрісі энергиясының тығыздығы
гармоникалық
заңдылықпен өзгереді. Электромагнитті
толқынды үдемелі қозғалатын зарядталған
бөлшек шығарады. Олай болса,толқынның
электр өрісінің кернеулігі мен магнит
индукциясы үдеуге тура пропорционал. Электр
өрісі энергиясының тығыздығы
![]()
мен магнит өрісінің энергиясының тығыздығы
![]()
өзара
тең. Онда электромагниттік өріс
энергиясының тығыздығы ![]() болады.
Ендеше, электр өрісінің кернеулігі
және магнит өрісінің индукциясы
болады.
Ендеше, электр өрісінің кернеулігі
және магнит өрісінің индукциясы ![]() және
және ![]() екенін
ескерсек, өрістің энергия
тығыздықтары
екенін
ескерсек, өрістің энергия
тығыздықтары ![]() және
және ![]() жиіліктің
төртінші дәрежесіне пропордионал екені
шығады.
жиіліктің
төртінші дәрежесіне пропордионал екені
шығады.
Электромагниттік
толкын ағынының тығыздығы немесе толкынның
интенсивтілігі ![]() жиіліктің төртінші
дәрежесіне пропорционал. Электромагниттік
өрістің тербеліс жиілігі неғұрлым
жоғары болса, толқынның интенсивтілігі,
яғни бірлік ауданға келетін қуат соғұрлым
артады.
жиіліктің төртінші
дәрежесіне пропорционал. Электромагниттік
өрістің тербеліс жиілігі неғұрлым
жоғары болса, толқынның интенсивтілігі,
яғни бірлік ауданға келетін қуат соғұрлым
артады.
13. Сыртқы өрістергі дипольдің энергиясы.
Қозғалмайтын
зарядтардың электр өрiсiн электростатикалық
деп атайды. Ол тек электр зарядтарынан
пайда болады және уақыт бойынша
өзгермейдi. Электр өрiсi осы зарядтармен
қоршаған кеңiстiкте бар болады және
онымен үздiксiз байланыста болады.
Электр диполiнiң негiзгi сипаттамасы
диполь (электр) моментi деп аталатын
векторлық физикалық шама болып табылады.
Бұл моменттiң модулi заряд q модулiнiң
арақашықтыққа L көбейтiндiсiне тең: .
Сыртқы электростатикалық өріске
орналасқан электрлік дипольдің
энергиясын қарастырсақ. Алдымен сырты
электростатикалық өрісте орналасқан
екі дипольді аламыз. Олардың кернеулігі
E1 және E2 тең. Ал потенциалы φ1
және φ2
тең деп аламыз. Сыртқы электростатикалық
өріске орналасқан электрлік дипольдің
энергиясы мынаған тең болады: U=
-eφ1+eφ2=e{φ2-
φ1}=e.δφ
/δl.l=Pgradlφ,
E=-gradφ,
-gradlφ=El,
U=pEl, U= -pEl=-(pE), p↑↑E.
14. Электрстатикалық өрістегі механикалық күштер.
Электрстатикалық
өрісте сыншы Q0 зарядты
шексіз аз ![]() орын
ауысты-руда кулондық күштердің атқаратын
элементар жұмысы:
орын
ауысты-руда кулондық күштердің атқаратын
элементар жұмысы:
![]() .
(104)
.
(104)
Нүктелік Q зарядтың
электрстатикалық өрісінде Q0 зарядтың
шексіз аз ![]() орын
ауыстыруында атқарылатын элементар
жұмыс:
орын
ауыстыруында атқарылатын элементар
жұмыс:
![]() ,
,
ал 1 нүктеден 2 нүктеге орын ауыстыруда атқарылатын жұмыс:
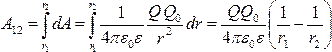 .
.
Кез келген L тұйық контур бойында Q заряд айнала қозғалғанда:
![]() .
(105)
.
(105)
![]() векторының
циркуляциясы туралы теорема: Электрстатикалық
өріс кернеулігі векторының кез келген
тұйық контур бойымен циркуляциясы
нөлге тең болады:
векторының
циркуляциясы туралы теорема: Электрстатикалық
өріс кернеулігі векторының кез келген
тұйық контур бойымен циркуляциясы
нөлге тең болады:
![]() .
(106)
.
(106)
Электрстатикалық
өріс құйынсыз
болғандықтан, Стокс теоремасына
сәйкес, ![]() кернеулігі
мына шартты қанағаттандырады:
кернеулігі
мына шартты қанағаттандырады: ![]() .
Бұл вакуумде және затта тек электрстатикалық
өріс үшін ғана орындалады.
.
Бұл вакуумде және затта тек электрстатикалық
өріс үшін ғана орындалады.
Сыншы нүктелік Q0 зарядтың нүктелік Q1, Q2 , Q3 , ..., QN зарядтар жүйесінің өрісіндегі потенциалдық энергиясыжеке зарядтарға қатысты потенциалдық энергиялардың қосындысына тең:
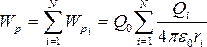 .
(107)
.
(107)
Электрстатикалық өрістің потенциалы–сан жағынан өрістің нақты нүктесінде орналасқан бірлік зарядтың потенциалдық энергиясына тең:
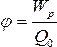 .
(108)
.
(108)
Электрстатикалық өріс күштерінің сыншы Q0 зарядты өрістің бір нүктесінен екінші нүктесіне орын ауыстыруда атқаратын жұмысы бастапқы және соңғы нүктелердің потенциалдар айырымын сыншы заряд шамасына көбейткенге тең:
![]() (109)
(109)
15.
Заттағы
Максвелл теңдеулерінің формальді
жүйесі, шекаралық шарттар.
Максвелл теңдеуі- классикалық электродинамиканың негізгі теңдеулері; кез келген ортадағы жэне вакуумдағы барлық электромагнит/электромагниттік кұбылыстарды толығымен сипаттайды, өріс көздерінің, электр зарядының жэнетоктардың орналасуы мен козғалысы аркылы электромагниттік өрісті сипатгайтын шамалар өзгерісін байланы- стыратын төрт тендеулер жүйесінен тұрады.Электромагниттік өріс теориясының негізін Максвелл теңдеулері деп аталатын теңдеулер жүйесі құрайды. Бұл теорияныңматематикалық аппараты күрделіболғандықтан, олтеңдеулердіқарастырмаймыз.
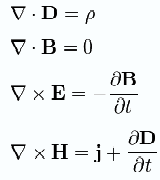
Изоторпты
және
дисперция
жоқ
ортадағы
Максвелл
теңдеулері: 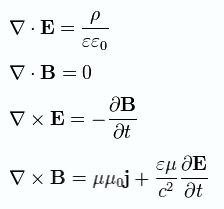
16.Вакуумдағы магнитстатиканың теңдеулері, олардың түсіндірмесі. Векторлық потенциал.
Уақыттан тәуелсіз магнит өрісі магнитстатикалық өріс д.а. Бұл жағдайда магнит өрісін электр өрісінен бөліп қарауға болады. Магнитстатикалық өріс үшін, Максвелл теңдеулерін келтірейік
-
rotH=j (1.1)
-
divB=0 (1.2)
B=µaH (1.3)
Bn2-Bn1=0 (1.4)
Hr2-Hr1= iбет (1.5)
1.1-теңдеуі магнитстатикалық өрістің потенциалдық емес құйынды өріс екендігін білдіреді.
1.2-теңдеуі магнит индукция сызықтарының тұйық екендігін білдіреді.
1.3-өрнегі магнит өрісі кернеулігін магнит индукциясымен байланысты.
1.4 және 1.5 екі екі ортаның шекаралық шарттарын өрнектейді.
1.4-өрнегі екі орта шекарасында магнит индукциясының нормаль құраушысының үзіліссіздігін білдіреді.
1.5- екі орта шекарасында магнит өрісі кернеулігі немесе жанама құраушысының мәндерінің үзілетіндігін көрсетеді.
Векторлық потенциал-құйынды векторлық өрісті сипаттауға арналып қолданылатын векторлық функция. Потенциал-физикалық күш өрістерінің кең көлемді тобын (электрлік, гравитатциялық, т.б.) және физикалық шамалардың векторымен көрсетілген өрістерін(сұйықтық жылдамдығының өрісі, т.б.) сипаттайтын ұғым. Әрбір векторлық шама а өзінің потенциалының градиентіне тең а=gradj. Мұндай жағдайда векторлық өрісті потенциялдық деп атайды. Векторлық өріс кестесінің әрбір нүктесінде вектор болатын функциямен сипаттайтын физикалық өріс.
17.Векторлық потенциалға арналған Пуассон теңдеуі, оның толық шешімі.
1.1 Магнит өрісінің векторлық потенциалы үшін Пуассон теңдеуі.
▼2А=-µaj (1.1)
1.1-Теңдеудің жалпы шешімін мына түрде жазуға болады.
▼2φ=
-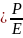 (1.2)
(1.2)
1.2-дегі Пуассон теңдеуін Оpтада электр заряды жоқ болған жағдайда қолданамыз.
18.Станционарлық магнит өрісінің магниттік дипольді жуықтаумен қарастырылуы.Магниттік момент.
Магниттік диполь электрлік диполь – шамалары тең, l ара қашықтығы өріс анықталатын нүктеге дейінгі қашықтықпен салыстырғанда едәуір аз. дипольдің электрлік моменті (дипольдік момент)– дипольдің иінімен бағыттас, заряд модулі мен иіннің көбейтіндісіне тең шама. Таралуы тұйық контурмен ағатын электр тогы жасаған магнит өрісінің таралуымен сәйкес келетін өрісті жасайтын, өлшемі өзінен өрістің қарастырылатын нүктесіне дейінгі қашықтықпен салыстырғанда өте кіші болатын магнит өрісінің кезі.
Магниттік момент — заттың магниттік қасиеттерін сипаттайтын негізгі шама. Электр-магниттік құбылыстардың классикалық теориясына сәйкес магнетизмнің (Магниттік моменттің) көзі электр макротоктар және микротоктар (атомдық) болып табылады. Магнетизмнің қарапайым көзі ретінде тұйық ток алынады. Электр-магнит өрістің классикалық теориясы және тәжірибелік деректер бойынша тұйық токтың (тогы бар контурдың) магнит әсері ток күші (і) мен контур ауданының () көбейтіндісі (М) белгілі болғанда ғана анықталады:М=і/с (бірліктердің СГС жүйесінде).Анықтама бойынша М векторы Магниттік момент болып табылады. Оны электрлік диполь моментіне ұқсастырып, М=ml, түрінде жазуға болады: мұндағы m — контурдың эквиваленттік магнит заряды, l — қарама-қарсы таңбалы “магниттік зарядтардың” ара қашықтығы.
19)
Магнетиктер.
Магниттелу векторы. Магнетиктегі магнит
өрісінің векторлық потенциалы.
Магниттік өріске орналасқан бүкіл заттар магниттеледі. Кез келген дене магнетик болып саналады, яғни ол магниттік өріс әсерімен магниттелуге қабілетті. Осы құбылыстың механизмін түсіну үшін мына суретті қарастырайық:

Атомдағы электрон дөңгелек орбита бойынша қозғалады деп аламыз. Электрон орбитасы В векторға қатысты альфа бұрыш жасап қозғалса, онда ол В шеңберінде осындай қозғалыс жасайды деп дәлелдеуге б-ды.Осылайша атомның электрондық орбиталары сыртқы магниттік өріс әсерімен, дөңгелек токқа эквивалентті прецессиялық қозғалыс жасайды. Ленц ережесіне сәйкес, атомда сыртқы өріске қарама-қарсы бағытталған құраушы магниттік өріс пайда б-ды. Заттар магнетиктер, диамагнетиктер ж/е ферромагнетиктер деп бөлінеді.
Диэлектриктердің үйектелуін сандық сипаттауға ұқсас, магниттердің магниттелуін сипаттайтын векторлық шама-магниттелушілік (магниттелу) енгізілді:
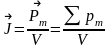
Pm-магнетиктің магниттік мезеті. V-магниттелу көлемі.
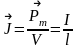
Магниттелу
біртекті өріс жағдайында : 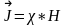
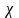 -
магниттік
қабылдағыштық.
-
магниттік
қабылдағыштық.
Магниттік өрістің векторлық потенциалы:
Векторлық потенциал - құйынды векторлық өрісті сипаттауға арналып қолданылатын векторлық функция.
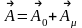
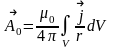
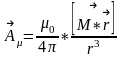
20) Магнит өрісінің энергиясы. Магнитстатикалық өрістің энергиясын токтар шамасы, өздік және өзара индукция коэффициенттері арқылы өрнектеу
Соленоидқа Е батареяны тұйықтасақ, ол арқылы ток жүреді, онда i тогы тұрақтанады да, соленоидтың орамдарында магнит өрісі туындайды. Батареяны R кедергімен алмастырсақ, ток кеми бастайды. Осы токпен істелетін жұмыс:
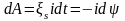 ,
егер L=const
болса,
dA=-Ldi.
,
егер L=const
болса,
dA=-Ldi.
Осыдан:
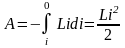
Сөйтіп
I тогы ағатын өткізгіш
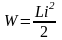 энергияға ие б-ды.
энергияға ие б-ды.
Магнитстатикалық өріс. Токтар шамасы арқылы:
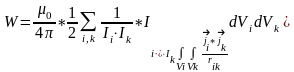
Өзара, өздік индукция коэф. арқылы:
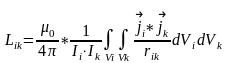
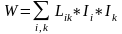
21) Магнитстатикалық өрістегі күштер. Шекаралық шарттар
Магнитстатика-тұрақты токтардың өзара әсерлесуін магнит өрісі арқылы зерттейтін (есептейтін) классикалық физиканың бөлімі. Уақыттан тәуелсіз магнит өрісі магнитстатикалық өріс деп аталады. Бұл жағдайда магнит өрісін электр өрісінен бөліп қарауға болады. Магнитстатикалық өріс потенциалдық емес, ол-құйынды өріс. Магнитстатикада Био-Савар-Лаплас заңы, магнит өрісі циркуляциясы туралы теорема, Лоренц, Ампер күштері формула-ы қолданылады.
Бөгде
күштер әсер ететін жағдайдағы Ом заңы:
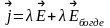
Джоуль-Ленц:
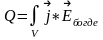
Био-Савар-Л.:
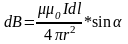
Екі
токтың өзара әсері:
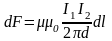
Ампер: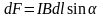
22. Электрмагниттік өріске арналған Максвелл теңдеулері жүйесінің интегралдық және дифференциалдық түрлері. Максвелл теңдеулерінің физикалық мағынасы. Максвелл теңдеулері жүйесі қасиеттері.
Максвелл теңдеулерінің интегралдық түрі
Максвелл теңдеулері интегралдардың көмегңмен де жазылуы мүмкін:
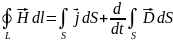

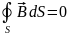
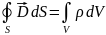
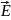 және
және
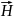 векторлары
өрістер айнымалы болса ғана байланыста
болатындығын ерекше атап өткен жөн.
Егер стационарлық өрістермен шектелсек,
яғни векторлар уақытқа тәуелсіз болса
векторлары
өрістер айнымалы болса ғана байланыста
болатындығын ерекше атап өткен жөн.
Егер стационарлық өрістермен шектелсек,
яғни векторлар уақытқа тәуелсіз болса
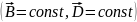 ,
онда өрістер теңдеуінен
,
онда өрістер теңдеуінен
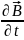 және
және
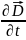 алынып тасталады. Сондықтан өрістің
дифференциалдық теңдеулер жүйесі екі
тәуелсіз жүйелерге ыдырайды.
алынып тасталады. Сондықтан өрістің
дифференциалдық теңдеулер жүйесі екі
тәуелсіз жүйелерге ыдырайды.
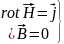 стационарлы
магнит өрісінің теңдеулерінің жүйесі
стационарлы
магнит өрісінің теңдеулерінің жүйесі
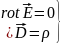 электростатикалық
өріс теңдеулерінің жүйесі.
электростатикалық
өріс теңдеулерінің жүйесі.
Осы екі теңдеулер жүйесінің бір-біріне тәуелсіздігі электростатикалық және стационарлық магнит өрістерін жеке-жеке зерттеуге мүмкіндік береді.
3 Максвелл теңдеулерінің дифференциалдық түрі
Максвелл теңдеулері сызықты дифференциалдық теңдеулер болғандықтан, оның дербес шешімдерінің қосындысы да сол теңдеулердің шешімі болады. Мұны векторлық өрістер үшін суперпозиция принципі деп атайды және есеп шығарған кезде жиі қолданылады. Теңдеулердің дифференциалдық түрін жазайық.
Максвелдің бірінші теңдеуі:
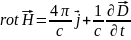
Максвелдің екінші теңдеуі:
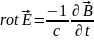
Индукция векторының дивергенциясы үшін теңдеу төмендегідей болады:
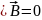
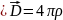
Үзіліссіз теңдеу
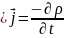
Материалдық теңдеу
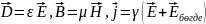
4 Максвелл теңдеулерінің физикалық мағынасы
Максвелл теңдеулерінің физикалық мағынасына тоқталу үшін оларды екі жұпқа топтастырайық:
Дифференциалды түрі
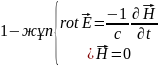
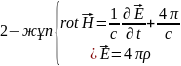
Интегралдық түрі
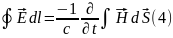
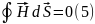
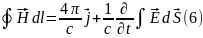
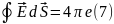
Токтар
мен зарядтардың үлестірулерін белгілі
деп алып, Максвелл теңдеулерінің
көмегімен
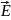 және
және
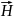 векторларының тәуелсіз алты құраушысын
табуға болады. Максвелдің сегіз скалярлық
дифференциалдық теңдеулер жүйесінде
алты тәуелсіз теңдеулер бар. (4) теңдеуі
Фарадейдің индукция заңының жалпылама
түрін беріп, уақыт бойынша магнит
өрісінің өзгерісі құйынды электр
өрісіні туғызатындығын көрсетеді. (5)
теңдеуі магнит өрісінің мінездемесі
соленойдалы және оның сызықтары тұйық
немесе шексіздікке кететіндігін
дәлелдейді. (6) теңдеуінен құйынды магнит
өрісі зарядтардың қозғалысынан және
уақыт бойынша электр өрісінің өзгерісінен
туындайтындығын көреміз. (7) теңдеуі
электр өрісінің көзі электр зарядтары
болып табылатындығын көрсетеді.
векторларының тәуелсіз алты құраушысын
табуға болады. Максвелдің сегіз скалярлық
дифференциалдық теңдеулер жүйесінде
алты тәуелсіз теңдеулер бар. (4) теңдеуі
Фарадейдің индукция заңының жалпылама
түрін беріп, уақыт бойынша магнит
өрісінің өзгерісі құйынды электр
өрісіні туғызатындығын көрсетеді. (5)
теңдеуі магнит өрісінің мінездемесі
соленойдалы және оның сызықтары тұйық
немесе шексіздікке кететіндігін
дәлелдейді. (6) теңдеуінен құйынды магнит
өрісі зарядтардың қозғалысынан және
уақыт бойынша электр өрісінің өзгерісінен
туындайтындығын көреміз. (7) теңдеуі
электр өрісінің көзі электр зарядтары
болып табылатындығын көрсетеді.
Қасиеті;Максвелл теңдеулері – кез келген ортадағы электромагниттік құбылысты сипаттайтын классикалық макроэлектродинамиканың діңгекті теңдеулері.
Максвелл теңдеулері электр зарядтары мен токтардан, электр және магнит индукцияларынан туындаған электромагниттік өрістердің өзара байланыстарын сипаттайды.
23. Электрмагниттік өрістің потенциалдары
Сан мәні зарядты өpicтiң берілген нүктесінен шексіздікке дейін қозғаған кезде істелетін жұмыстың осы зарядтың шамасына катынасына тең болатын энергетикалық сипаттаманы электростатикалық өрістің потенңиалы деп атайды;
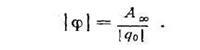
Бұл анықтама теория жүзіндегі анықтама болып табылады. Зарядты жер бетінен өpicтiң берілген нүктесіне дейін қозғаған кезде істелетін жұмыстың осы зарядтың шамасына катынасынэлектростатикалық өрістің потенңиалы деп атайды.
Зарядты
өpicтiң потенңиалы ![]() 1 болатын
нүктесіен потенңиалы
1 болатын
нүктесіен потенңиалы ![]() 2 болатын
нүктесіне дейін қозғаған кезде істелетін
жұмыстың осы заряд шамасына
қатынасын потенңиалдар
айырымы (ф1 —ф2)
деп атайды:
2 болатын
нүктесіне дейін қозғаған кезде істелетін
жұмыстың осы заряд шамасына
қатынасын потенңиалдар
айырымы (ф1 —ф2)
деп атайды:
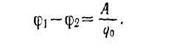
24) Лоренц шарттары. Потенциалдарға арналған теңдеулер
Қозғалыстағы зарядталған бөлшектерге магнит өрісі тарапынан әсер ететін күш Лоренц күші деп аталады.
FЛ = qυB sin α.
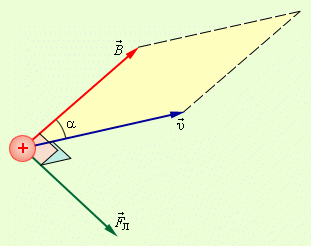
Мұндағы - В және векторлары арасындағы бұрыш. Ампер күшінің бағыты секілді, Лоренц күшінің бағыты сол қол ережесімен анықталады.
Б
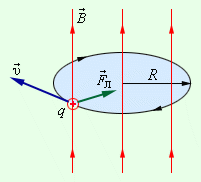 іртекті
магнит өрісінде оның индукциясына
перпендикуляр
жылдамдықпен қозғалған зарядты бөлшекке
модулі жағынан тұрақты, жылдамдыққа
перпендикуляр бағытталған Лоренц күші
әсер етеді. Лоренц күшінің әсерімен
бөлшек центрге тартқыш үдеу алады және
шеңбер бойымен қозғалады, мұнда Лоренң
күші жұмыс істемейді. Шеңбердің радиусы:
іртекті
магнит өрісінде оның индукциясына
перпендикуляр
жылдамдықпен қозғалған зарядты бөлшекке
модулі жағынан тұрақты, жылдамдыққа
перпендикуляр бағытталған Лоренц күші
әсер етеді. Лоренц күшінің әсерімен
бөлшек центрге тартқыш үдеу алады және
шеңбер бойымен қозғалады, мұнда Лоренң
күші жұмыс істемейді. Шеңбердің радиусы: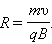
Электр тогы-зарядалған бөлшектердің реттелген бағытталған қозғалысы.Токтың бағытына оң зарядталған бөлшектердің қозғалыс бағыты алынады.Токтың әсері: 1)боймен ток жүрген өткізгіш қызады.2)химиялық әсері байқалады.3)Магниттік әсері байқалады.Электр тогы болу үшін мына шарттар орындалу қажет:1)Зарядталған бөлшектер q.2)Өріс тарапынан әсер ететін күш болу керек(F=qE).3)Электр өрісі Е.4)Потенциял айырмасы U болу керек.
|
|
Сыртқы
магнит өрісі ![]() -де
орналасқан ток элементі Idl -ді
қарастырайық.Бұл векторлардың арасындағы
бұрышыт
-де
орналасқан ток элементі Idl -ді
қарастырайық.Бұл векторлардың арасындағы
бұрышыт ![]() болсын.Ампер
күшіне сәйкес Idl элементіне мынадай
күш әсер етеді
болсын.Ампер
күшіне сәйкес Idl элементіне мынадай
күш әсер етеді
dF=BIdl ![]()
мұндағы ток күші
I= ![]() q=lN
q=lN
Осы
бірінші өрнекті екіншісіне қою
нәтижесінде мынаны шығарып
аламыз:dF=BdlN ![]() зарядтың
қозғалыс жылдамдығы болатындықтан
жоғарыдағы өрнектен
зарядтың
қозғалыс жылдамдығы болатындықтан
жоғарыдағы өрнектен
Fn= ![]()
Векторлық формада өрнегі былайша жазылады,яғни
![]()
Магнит
өрісінде қозғалатын зарядқа әсер ететін
күш ![]() -ді
Лоренц анықтаған, сондықтан бұл Лоренц
күші деп
аталған.Сол қол немесе бұранда ережесі
бойынша бұл күштің
-ді
Лоренц анықтаған, сондықтан бұл Лоренц
күші деп
аталған.Сол қол немесе бұранда ережесі
бойынша бұл күштің![]() және
және ![]() векторлары
жататын жазықтыққа перпендикуляр
болатынын байқйамыз.Сондықтан бұль
күш жылдамдықтың шамасын өзгерте
алмайды,тек оның бағытын ғана өзгерте
алады.Олай болса, Лоренц күші центрге
тартқыш күш болып табылады:
векторлары
жататын жазықтыққа перпендикуляр
болатынын байқйамыз.Сондықтан бұль
күш жылдамдықтың шамасын өзгерте
алмайды,тек оның бағытын ғана өзгерте
алады.Олай болса, Лоренц күші центрге
тартқыш күш болып табылады:
![]() =const
және
=const
және ![]() болғанда
болғанда
q ![]() B=
B= ![]()
Өрнек ![]() өрісіндегі
зарядтың қозғалыс параметрлерін табуға
арналған өрнек болады
өрісіндегі
зарядтың қозғалыс параметрлерін табуға
арналған өрнек болады
Электр
өрісінің потенциалы –
скалярлық шама, өрістің берілген
нүктесіндегі потенциалық энергияның,
сыншы зарядқа қатынасы
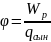 .
.
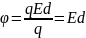 .Бұдан
потенциал өрістің энергетикалық
сипаттамасын беретін физикалық шама
екенін көреміз. Өрістің күштік
сипаттамасы кернеулік және оның
энергетикалық сипаттамасы – потенциалдың
арасында электростатикалық өрістің
потенциалдығына негізделген байланыс
бар.
Потенциалды күш өрісінде потенциалдық
энергия мен күш арасындағы
байланыс
мына түрде берілген
.Бұдан
потенциал өрістің энергетикалық
сипаттамасын беретін физикалық шама
екенін көреміз. Өрістің күштік
сипаттамасы кернеулік және оның
энергетикалық сипаттамасы – потенциалдың
арасында электростатикалық өрістің
потенциалдығына негізделген байланыс
бар.
Потенциалды күш өрісінде потенциалдық
энергия мен күш арасындағы
байланыс
мына түрде берілген
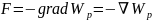 .мұнд.
.мұнд.
 ,
оның түрі
,
оның түрі
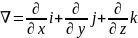 ,
осыдан
,
осыдан
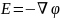 .
Мұндағы «минус» таңбасы Е векторының
бағыты әрқашан да потенциалдың кемуіне
қарай бағытталғандығын көрсетеді.
.
Мұндағы «минус» таңбасы Е векторының
бағыты әрқашан да потенциалдың кемуіне
қарай бағытталғандығын көрсетеді.
Нүктелік
заряд потенциялының формуласы
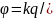 Er.
Er.
Потенциялдар айырмасын өлшейтін құрал-электрометр деп аталады. Потенциал[1] (потенциалдық функция) — физикалық күш өрістерінің кең көлемді тобын (электрлік, гравитациялық, т.б.) және физикалық шамалардың вектормен көрсетілген өрістерін (сұйықтық жылдамдығының өрісі, т.б.) сипаттайтын ұғым. Әрбір векторлық шама а өзінің потенциалының градиентіне тең: а=gradj. Мұндай жағдайда векторлық өрісті потенциалдық деп атайды. Потенциал векторлық өрісті сипаттау үшін көмекші функция ретінде енгізіледі. Термодинамикада потенциал берілген жүйе күйін сипаттаушы макропараметрлерге байланысты функция ретінде қарастырылады. Потенциал арқылы термодинам. жүйенің барлық қасиетін анықтауға болады. Физикада потенциал ұғымының басқа мағынасы да бар. Мысалы, электр өрісінде ол бірлік зарядты электр өрісінің берілген бір нүктесінен шексіздікке тасуға кеткен жұмысына тең.
Потенциал(Педагогика) - қандай да болсын міндетті шешу үшін, белгілі мақсатқа жету үшін пайдаланылуы мүмкін қайнар-көздер, мүмкіндіктер, құралдар, қорлар, белгілі бір саладағы жеке тұлғаның, қоғамның, мемлекеттің мүмкіндіктері.[2]
Векторлық потенциал - құйынды векторлық өрісті сипаттауға арналып қолданылатын векторлық функция.[1]
векторный потенциал — это векторное поле, ротор которого равен заданному векторному полю. Он аналогичен скалярному потенциалу, который определяется как скалярное поле, градиент которого равен заданному векторному полю.
Формально, если v — векторное поле, векторным потенциалом называется векторное поле A такое, что
![]()
Если A является векторным потенциалом для поля v, то из тождества
![]()
(дивергенция ротора равна нулю) следует
![]()
то есть v должно быть соленоидальным векторным полем.
Векторный потенциал в физике[править | править вики-текст]
Основная статья: Векторный потенциал электромагнитного поля
Уравнения Максвелла[править | править вики-текст]
Одним
из способов записи уравнений
Максвелла является
формулировка в терминах векторного и
скалярного потенциалов. Векторный
потенциал ![]() вводится
таким образом, что
вводится
таким образом, что
![]() (в
системе СИ).
(в
системе СИ).
При
этом уравнение ![]() удовлетворяется
автоматически.
удовлетворяется
автоматически.
Подстановка
выражения для ![]() в
в
![]()
приводит к уравнению
![]() ,
,
согласно
которому, так же как и в электростатике вводится
скалярный потенциал. Однако теперь
в ![]() вносят
вклад и скалярный и векторный потенциал:
вносят
вклад и скалярный и векторный потенциал:
![]()
Из
уравнения ![]() следует
следует
![]()
Используя
равенство ![]() ,
уравнения для векторного и скалярного
потенциалов можно записать в виде
,
уравнения для векторного и скалярного
потенциалов можно записать в виде
![]()
![]()
Скалярный
потенциал векторного
поля ![]() (чаще
просто потенциал векторного
поля) — это скалярная функция
(чаще
просто потенциал векторного
поля) — это скалярная функция ![]() такая,
что во всех точках области определения
поля
такая,
что во всех точках области определения
поля
![]()
где ![]() обозначает градиент
обозначает градиент ![]() .
В физике обычно потенциалом называют
величину, противоположную по знаку
(потенциал силы, потенциал электрического
поля).
.
В физике обычно потенциалом называют
величину, противоположную по знаку
(потенциал силы, потенциал электрического
поля).
25. Электрмагниттік өрістің энергия ағынының тығыздығы және энергиясының тығыздығы..
Электромагниттік толқындарды анықтау мүмкіндігі, оларды энергияны тасымалдайтынын
көрсетеді. Элмгнттк толқындар энерг.-ң w көл.-к тығ.-ғы, w(эл.) электр w(м) магниттік өрістердің көл.-к тығыздығынан қалыптасады: w = w(эл)+w(эл)= (ε0ε)E²/2 + μ0μH²/2, w(эл)=W/V=ED/2
ε0εE=
μ0μH² осыны ескере отырып , уақыттың
әрбір мезетіндегі эл. ж\е маг.-к өрістер
энерг.-ң көлемдік тғздқнң бірдейлігін
аламыз, яғни w(эл)=w(м). Сондықтан былай
болады: w=2 w(эл)= ε0ε
E²=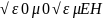 .
.
Энергияның тығыздығын ортадағы толқындардың таралу жылд.-на көбейтіп, энергия ағыны тығыздығының модулін аламыз: S=wv=EH, өйткені Е ж/e Н векторлары өзара перпенд.-р және толқындардың таралу бағытымен оң бұрандалық жүйені құрайды, сондықтан векторлар [ЕН] бағыты, энергияларды тасымалдау бағытымен сәйкес келеді, ал бұл вектордың модулі ЕН-ге тең. Элмгнттк энергия ағынының тығыздық векторы Умов-Поитинг векторы деп аталады: S=[EH]
26. Идеал біртекті диэлектриктегі электрмагниттік толқындық теңдеу. Жазық монохромат толқындар, олардың сипаттамалары.
электрмагниттік
толқындар–көлденең толқындар. айнымалы
электр өрісінің кернеулігі ![]() векторы
мен айнымалы магнит өрісінің
кернеулігі
векторы
мен айнымалы магнит өрісінің
кернеулігі ![]() векторы
өзара перпендикуляр және толқынның
векторы
өзара перпендикуляр және толқынның
т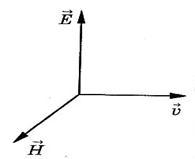 аралу
жылдамдығы
аралу
жылдамдығы ![]() вектор
вектор
ына перпендикуляр (83-сурет).
электрмагниттік
толқында ![]() және
және ![]() векторлары
бірдей фазада тербеледі. олардың лездік
мәндері кез келген нүктеде мына
қатынаспен байланысқан:
векторлары
бірдей фазада тербеледі. олардың лездік
мәндері кез келген нүктеде мына
қатынаспен байланысқан:![]()
![]() және
және ![]() векторлары
үшін толқындық теңдеулер:
векторлары
үшін толқындық теңдеулер:
![]()
мұндағы
![]() лаплас
операторы.
лаплас
операторы.
![]() және
және ![]() үшін
толқындық теңдеулер:
үшін
толқындық теңдеулер:
![]() осы
теңдеулерге сәйкес жазық
монохромат толқындардың теңдеулері:
осы
теңдеулерге сәйкес жазық
монохромат толқындардың теңдеулері:
![]() .
.
мұндағы
![]() толқынның
электр өрісі кернеулігінің амплитудасы;
толқынның
электр өрісі кернеулігінің амплитудасы;
![]() толқынның
магнит өрісі кернеулігінің амплитудасы;
толқынның
магнит өрісі кернеулігінің амплитудасы;
![]() толқындық
сан;
толқындық
сан;
![]() тербелістердің x=0
координатқа сәйкес бастапқы фазалары.
тербелістердің x=0
координатқа сәйкес бастапқы фазалары.
27: Өткізгіш ортадағы электрмагниттік толқындар
25-26 да жауабы
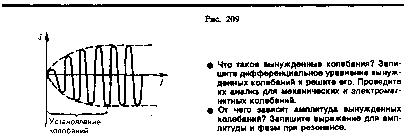
28. Контурдағы мәжбүр электрмагниттік тербелістердің дифференциалдық
теңдеуі және оның шешімі.
Сыртқы
периодты өзгеретіін күштердің әсерімен
немесе сыртқы периодты өзгеретін ЭҚКның
әсерінен туындайтын тербеліс- мәжбүр
эектромагниттік тербеліс деп аталады.
Мәжбүр тербеліс белгіленген режимде
ω
жиілікпен тербеледі, фаза мен амплитудаға
тәуелді. Электромагниттік тербеліс
үшін
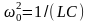 және
и
және
и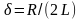 ескере
отырып,
ескере
отырып,
![]()
Т бойыншы дифференциалдай отырып, орнатылған тербеліс кезіндегі контурдағы токтыы есеептеййміз:
![]()
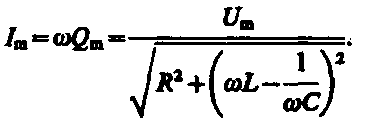
Бұл формуланы келесідей жазуға болады:
![]()
Мұндағы = – /2
![]()
Бұл формулада ток фаза бойынша артта қалатын болса
(>0), L>1/(С), ал керісінше болса (<0), если L<1/(С).
29. Контур элементтеріндегі кернеулер және тізбектегі ток күші үшін
резонанстық қисықтар және олардың талдамы. Контурдың сапалылығы.
Резонанс (лат. resono, фр. resonance — үн қосу, дыбыс қайтару) — периодты түрде сырттан әсер етуші күштің жиілігі тербелмелі жүйенің меншікті жиілігіне жақындағанда сол тербелмелі жүйедегі еріксіз тербелістер амплитудасының күрт арту құбылысы; мәжбүр етуші күштің жиілігі жүйе тербелісінің меншікті жиілігіне жуықтаған кезде жүйедегі мәжбүр тербеліс амплитудасының кенеттен артып кету кұбылысы.[1]
Резонансты алғаш рет механика және акустикалық құбылыс ретінде италиян ғалым Г.Галилей, ал электр-магниттік жүйелерде, мысалы, тербелмелі контур арқылы ағылшын ғалымы Дж.Максвелл (1831 — 1879) қарастырған (1868). Жүйеге гармондық сыртқы күш (F) әсер еткенде массасы m-ге тең дененің қозғалыс теңдеуі мына түрде жазылады:
мұндағы F0 — сыртқы күштің амплитудасы, v — сыртқы әсердің жиілігі, х — ауытқу, — масса жылдамдығы, a— масса үдеуі, b — үйкеліс коэфф., k — қатаңдық коэфф. Бұл теңдеудің шешуі болады. Мәжбүрлеуші күштің жиілігі тербелмелі жүйенің жиілігіне жақындаған сайын тербеліс амплитудасының қалай өсетіні осы формуладан айқын көрінеді.
30.Реактивті және толық кедергі. Айнымалы ток тізбегі үшін Ом заңы
Бір-біріне
тізбектей
жалғанған индуктивтігі ![]() катушкадан, сыйымдылығы
катушкадан, сыйымдылығы ![]() конденсатордан және кедергісі
конденсатордан және кедергісі ![]() резистордан тұратын
тізбектің
қысқыштарына
резистордан тұратын
тізбектің
қысқыштарына ![]() айнымалы
кернеу
түсірейік
(2.15-сурет). Ток
күшінің
айнымалы
кернеу
түсірейік
(2.15-сурет). Ток
күшінің ![]() лездік
мәні де,
лездік
мәні де, ![]() амплитудалық
мәні де тізбектей жалғанған тізбектің
барлық бөлігінде бірдей болады. Ал ток
көзінің полюстеріндегі лездік кернеу
оның жеке бөліктеріндегі кернеудің
лездік мәндерінің қосындысына
тең
амплитудалық
мәні де тізбектей жалғанған тізбектің
барлық бөлігінде бірдей болады. Ал ток
көзінің полюстеріндегі лездік кернеу
оның жеке бөліктеріндегі кернеудің
лездік мәндерінің қосындысына
тең![]() (2.14)Тізбектей
жалғанған тізбектің барлық бөлігіндегі
токтың тербелісі
(2.14)Тізбектей
жалғанған тізбектің барлық бөлігіндегі
токтың тербелісі![]() заңы
бойынша өзгерсін.Қарастырып отырған
тізбекте еріксіз электромагниттік
тербелістер, яғни айнымалы ток пайда
болады. Резистордағы, конденсатордағы
және катушкадағы кернеудің амплитудаларын
сәйкесінше
заңы
бойынша өзгерсін.Қарастырып отырған
тізбекте еріксіз электромагниттік
тербелістер, яғни айнымалы ток пайда
болады. Резистордағы, конденсатордағы
және катушкадағы кернеудің амплитудаларын
сәйкесінше ![]() және
және ![]() деп
белгілеп, оларды векторлық диаграммаға
салайық (2.15-сурет). Ток күшінің амплитудасын
горизонталь ось бойымен бағытталған
вектор түрінде кескіндейік. Онда
горизонталь ось пен әрбір кернеу
амплитудасы векторының арасындағы
бұрыш ток күшімен ғана сәйкес кернеу
тербелістерінің фазалық айырымына тең
болады.Активті
кедергідегі кернеудің тербеліс
фазасы ток күшінің тербеліс
фазасымен сәйкес келеді, ал конденсаторда
кернеудің тербелісі ток күшінің
тербелісінен фаза бойынша
деп
белгілеп, оларды векторлық диаграммаға
салайық (2.15-сурет). Ток күшінің амплитудасын
горизонталь ось бойымен бағытталған
вектор түрінде кескіндейік. Онда
горизонталь ось пен әрбір кернеу
амплитудасы векторының арасындағы
бұрыш ток күшімен ғана сәйкес кернеу
тербелістерінің фазалық айырымына тең
болады.Активті
кедергідегі кернеудің тербеліс
фазасы ток күшінің тербеліс
фазасымен сәйкес келеді, ал конденсаторда
кернеудің тербелісі ток күшінің
тербелісінен фаза бойынша ![]() -ге
озады. Сондықтан (2.14) өрнегін былай
жазуға болады:
-ге
озады. Сондықтан (2.14) өрнегін былай
жазуға болады: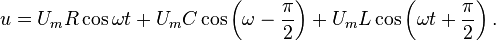
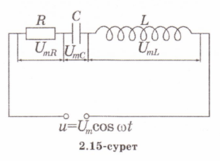
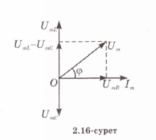 Түсірілген
кернеудің
Түсірілген
кернеудің ![]() амплитудасын
векторлардың қосындысы ретінде табуға
болады, яғни
амплитудасын
векторлардың қосындысы ретінде табуға
болады, яғни![]() 2.16-суреттен,
барлық тізбектегі кернеудің амплитудасы
Пифагор теоремасы бойынша
2.16-суреттен,
барлық тізбектегі кернеудің амплитудасы
Пифагор теоремасы бойынша ![]() тең.
Ом заңына сәйкес
тең.
Ом заңына сәйкес![]() және
және ![]() сондықтан
сондықтан![]() осыдан
осыдан![]() (2.15)Бұл
айнымалы токтың толық тізбегі үшін Ом
заңы.
(2.15)Бұл
айнымалы токтың толық тізбегі үшін Ом
заңы. ![]() және
және ![]() болғандықтан,
(2.15) формуласын былай жазуға
болады.
болғандықтан,
(2.15) формуласын былай жазуға
болады. ![]()
![]() кедергісін
реактивті кедергі, ал
кедергісін
реактивті кедергі, ал ![]() кедергісі
айнымалы ток тізбегінің толық кедергісі
деп аталады.
кедергісі
айнымалы ток тізбегінің толық кедергісі
деп аталады. ![]() фазалар
айырымын векторлық диаграмманы колданып
анықтауға болады:
фазалар
айырымын векторлық диаграмманы колданып
анықтауға болады:![]() немесе
немесе ![]() (2.16)Ток пен кернеудің әсерлік
мәндерін колдансақ, (2.15) өрнегін былай
жазуға болады:
(2.16)Ток пен кернеудің әсерлік
мәндерін колдансақ, (2.15) өрнегін былай
жазуға болады: ![]() Тізбекте
конденсатор жоқ кездегі векторлық
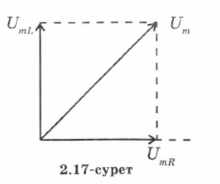
диаграмманы салайық (2.17-сурет). Бұл
дербес жағдайда
Тізбекте
конденсатор жоқ кездегі векторлық
диаграмманы салайық (2.17-сурет). Бұл
дербес жағдайда ![]()
![]()
 Егер
(2.15) пен (2.16) өрнектерінде
Егер
(2.15) пен (2.16) өрнектерінде ![]() яғни
яғни ![]() деп
алсақ, соңғы екі формула шығады. Олай
болса, тізбекте конденсатор жоқ болса,
сыйымдылық
деп
алсақ, соңғы екі формула шығады. Олай
болса, тізбекте конденсатор жоқ болса,
сыйымдылық ![]() нөлге
емес, шексіздікке тең екен. Шынында да,
егер тізбектегі конденсатордың
астарларын бір-біріне шексіз жақындатса,
конденсаторды жоқ деп есептеуге болады.
Ал жазық конденсатордың сыйымдылығы
нөлге
емес, шексіздікке тең екен. Шынында да,
егер тізбектегі конденсатордың
астарларын бір-біріне шексіз жақындатса,
конденсаторды жоқ деп есептеуге болады.
Ал жазық конденсатордың сыйымдылығы ![]() Бұл
формуладан егер
Бұл
формуладан егер ![]() болса,
болса, ![]() шығады.
шығады.
Генератордан алынатын энергия тек активті кедергіде ғана жылу энергиясы түрінде бөлініп шығады. Реактивті кедергіде энергияжұтылмайды. Реактивті кедергіде периодты түрде электр өрісінің энергиясы магнит өрісінің энергиясына айналып, түрленіп отырады. Периодтың бірінші ширегінде, конденсатор зарядталып жатқанда энергия тізбекке электр өрісінің энергиясы түрінде түсіп, жинақталады. Ал периодтың келесі ширегінде, конденсатор разрядталып жатканда, энергия қайтадан магнит өрісінің энергиясы түрінде желіге қайтарылады.[2] Тагы да R=p*l/S - ке тең болады.
31.Кернеу резонансы. Резонанстық жиілік.
Айнымалы
ток тізбегінің
толық кедергісі ![]() өрнегімен
анықталатыны белгілі болды. Бұл
формуладағы индуктивтік
кедергі мен сыйымдылық
кедергі бір-біріне тең болса, толық
кедергі
өрнегімен
анықталатыны белгілі болды. Бұл
формуладағы индуктивтік
кедергі мен сыйымдылық
кедергі бір-біріне тең болса, толық
кедергі ![]() ең
аз мәнге ие болатынын көреміз. Сонымен,
егер
ең
аз мәнге ие болатынын көреміз. Сонымен,
егер![]() (2.17)болса,
(2.17)болса, ![]() .
Мұндай жағдайда ток пен кернеудің тербеліс
фазаларының айырымы:
.
Мұндай жағдайда ток пен кернеудің тербеліс
фазаларының айырымы:![]() яғни
ток пен кернеу тербелістері бірдей
фазада жүреді. Активті кедергідегі
кернеу тізбекке түсірілген кернеуге
тең
яғни
ток пен кернеу тербелістері бірдей
фазада жүреді. Активті кедергідегі
кернеу тізбекке түсірілген кернеуге
тең ![]() ,
ал конденсатордағы
,
ал конденсатордағы ![]() кернеу
мен катушкадағы
кернеу
мен катушкадағы ![]() кернеу
амплитудалары бір-біріне тең және
фазалары қарама-қарсы. Ом заңы бойынша
ток амплитудасы
кернеу
амплитудалары бір-біріне тең және
фазалары қарама-қарсы. Ом заңы бойынша
ток амплитудасы![]() Бұл
өрнектен, егер активті кедергі
Бұл
өрнектен, егер активті кедергі ![]() аз
болса, ток
күшінің амплитудасы өте
үлкен мәнге ие болатынын көреміз.
Жоғарыда сипатталған құбылыс электр
тізбегіндегі резонанс деп
аталады. Резонанс байқалу үшін тізбекке
түсірілген кернеудің жиілігі (2.17)
өрнегін қанағаттандыру керек:
аз
болса, ток
күшінің амплитудасы өте
үлкен мәнге ие болатынын көреміз.
Жоғарыда сипатталған құбылыс электр
тізбегіндегі резонанс деп
аталады. Резонанс байқалу үшін тізбекке
түсірілген кернеудің жиілігі (2.17)
өрнегін қанағаттандыру керек:![]() Біз
активті кедергісі
Біз
активті кедергісі ![]() идеал
тербелмелі контурдың меншікті
тербелістерінің жиілігі
идеал
тербелмелі контурдың меншікті
тербелістерінің жиілігі ![]() өрнегімен
анықталатынын білеміз. Олай болса,
электр тізбегінде резонанс тізбекке
түсірілген сыртқы периодты кернеудің
жиілігі тізбектің меншікті жиілігіне
тең болғанда байқалады
өрнегімен
анықталатынын білеміз. Олай болса,
электр тізбегінде резонанс тізбекке
түсірілген сыртқы периодты кернеудің
жиілігі тізбектің меншікті жиілігіне
тең болғанда байқалады ![]() (2.19-сурет).
Осы кезде катушкадағы индуктивтік
кедергі конденсатордың сыйымдыльщ
кедергісіне тең болады:
(2.19-сурет).
Осы кезде катушкадағы индуктивтік
кедергі конденсатордың сыйымдыльщ
кедергісіне тең болады: ![]() .
Активті кедергі неғұрлым аз болса, ток
күшінің амплитудасы соғұрлым үлкен.
.
Активті кедергі неғұрлым аз болса, ток
күшінің амплитудасы соғұрлым үлкен.
2.19-суретте ![]() .
Егер активті кедергі шексіз аз болса
.
Егер активті кедергі шексіз аз болса ![]() →
→![]() ,
ток амплитудасы шексіз артады
,
ток амплитудасы шексіз артады ![]() →
→![]() .
Активті, индуктивтік және сыйымдылық
кедергілер тізбектей жалғанғанда
байқалатын резонансты кернеулер
резонансы немесе тізбекті резонанс
деп атайды. Себебі резонанс кезінде
токтың өсуімен
қатар, катушка мен конденсатордағы кернеулер
де күрт өседі. Тізбектей жалғанған
кезде конденсатор мен катушкадағы
кернеулер қарама-қарсы фазада тербеледі,
ал тізбектің барлық элементі арқылы
өтетін токтың бағыты бірдей,
сондықтан
.
Активті, индуктивтік және сыйымдылық
кедергілер тізбектей жалғанғанда
байқалатын резонансты кернеулер
резонансы немесе тізбекті резонанс
деп атайды. Себебі резонанс кезінде
токтың өсуімен
қатар, катушка мен конденсатордағы кернеулер
де күрт өседі. Тізбектей жалғанған
кезде конденсатор мен катушкадағы
кернеулер қарама-қарсы фазада тербеледі,
ал тізбектің барлық элементі арқылы
өтетін токтың бағыты бірдей,
сондықтан ![]() болғанда,
яғни резонанс кезінде кез келген уақыт
мезеті үшін
болғанда,
яғни резонанс кезінде кез келген уақыт
мезеті үшін ![]() .
Ал
.
Ал ![]() екенін
ескерсек, индуктивтік катушкадағы және
конденсатордағы кернеу тербелістерінің
амплитудасы былай есептеледі:
екенін
ескерсек, индуктивтік катушкадағы және
конденсатордағы кернеу тербелістерінің
амплитудасы былай есептеледі:![]() Сонымен,
Сонымен,![]() Тербелмелі
контурда
Тербелмелі
контурда ![]()
![]() қатынасы
орындалады, сондықтан конденсатор мен
катушкадағы кернеулер тізбекке
түсірілген кернеуден артық және
қатынасы
орындалады, сондықтан конденсатор мен
катушкадағы кернеулер тізбекке
түсірілген кернеуден артық және ![]() азайған
сайын арта түседі. Жалпы, активті
кедергісі
азайған
сайын арта түседі. Жалпы, активті
кедергісі ![]() аз
болғанда ғана резонанс құбылысын
қарастырады. Активті кедергінің үлкен
мәндерінде іс жүзінде резонанс
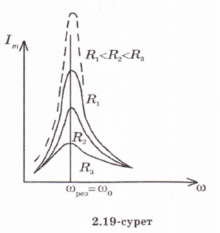
байқалмайды (2.20-сурет). Кернеулер
резонансын кандай да бір берілген
жиіліктегі кернеу тербелістерін күшейту
үшін пайдаланады. Кернеудің резонанстық
өсуі резонанстық жиілікке жуық өте аз
интервалда жүретін болғандықтан,
көптеген сигнал ішінен жиілігі сол
резонанстық жиілікке жуық бір ғана
сигнал бөліп алынады.
Мысалы, радиоқабылдағышта керекті
толқынды осылайша іздейді. Катушкалары
мен конденсаторлары бар электр
жүйелерінің изолядияларын есептегенде
де кернеулер резонансын ескеру керек,
әйтпесе электр тесілулері болуы мүмкін.
Механикалық тербелістердід резонансы
сыртқы периодты күштің жиілігі тербелмелі
жүйенің меншікті жиілігімен дәл келгенде
байқалатынын білеміз. Механикалық
тербелістерде үйкеліс күштеріэлектромагниттік
тербелістердегі активті кедергінің
рөлін атқарады.[1]
аз
болғанда ғана резонанс құбылысын
қарастырады. Активті кедергінің үлкен
мәндерінде іс жүзінде резонанс
байқалмайды (2.20-сурет). Кернеулер
резонансын кандай да бір берілген
жиіліктегі кернеу тербелістерін күшейту
үшін пайдаланады. Кернеудің резонанстық
өсуі резонанстық жиілікке жуық өте аз
интервалда жүретін болғандықтан,
көптеген сигнал ішінен жиілігі сол
резонанстық жиілікке жуық бір ғана
сигнал бөліп алынады.
Мысалы, радиоқабылдағышта керекті
толқынды осылайша іздейді. Катушкалары
мен конденсаторлары бар электр
жүйелерінің изолядияларын есептегенде
де кернеулер резонансын ескеру керек,
әйтпесе электр тесілулері болуы мүмкін.
Механикалық тербелістердід резонансы
сыртқы периодты күштің жиілігі тербелмелі
жүйенің меншікті жиілігімен дәл келгенде
байқалатынын білеміз. Механикалық
тербелістерде үйкеліс күштеріэлектромагниттік
тербелістердегі активті кедергінің
рөлін атқарады.[1]
32.Айнымалы ток тізбегіндегі қуат. Қуат коэффициенті. Ток күшінің және кернеудің әсерлік мәндері.
Айнымалы ток тізбегінде берілген уақыт мезетіндегі қуат ток күші мен кернеудің лездік мәндерінің көбейтіндісіне тең.
![]()
Бұл өрнекті түрлендіріп
![]() аламыз.
аламыз.
Бізге бір период ішіндегі орташа қуатты анықтау керек. Ол үшін уақытқа тәуелді тригонометриялық функциялардың орташа мәндерін табайық:
![]() онда
онда ![]()
Олай болса, қуатты анықтайтын өрнектегі екінші қосылғыштың орташа мәні нөлге тең. Сонымен, айнымалы ток тізбегінде орташа қуат:
![]() (2.18)
(2.18)
Бұл
теңдеуге ток пен кернеудің әсерлік
мәндерін қойып, ыңғайлы болу үшін
әсерлік мәндердің индексін
жазбай ![]() және
және ![]() деп
белгілесек,
деп
белгілесек,
![]() (2.19)
(2.19)
шығады.
(2.18) мен (2.19) өрнектеріндегі ![]() шамасы
қуат коэффициенті деп аталады. Осы
өрнек айнымалы токтың қуаты тек ток
күші мен кернеуге ғана емес, сонымен
қатар олардың тербеліс
фазаларының айырымына да тәуелді
екенін көрсетеді.
шамасы
қуат коэффициенті деп аталады. Осы
өрнек айнымалы токтың қуаты тек ток
күші мен кернеуге ғана емес, сонымен
қатар олардың тербеліс
фазаларының айырымына да тәуелді
екенін көрсетеді.
Егер тізбектегі
реактивті кедергі ![]() болса,
болса, ![]() ,
онда
,
онда ![]() ,
яғни бұрыннан белгілі тұрақты токтың
қуатының формуласын аламыз. Ал тізбекте
активті кедергі жоқ болса,
,
яғни бұрыннан белгілі тұрақты токтың
қуатының формуласын аламыз. Ал тізбекте
активті кедергі жоқ болса, ![]() онда
онда ![]() .
Тек реактиві кедергісі ғана бар тізбекте
орташа қуат нөлге тең. (2.18) формуласынан
қуатты өсіру үшін
.
Тек реактиві кедергісі ғана бар тізбекте
орташа қуат нөлге тең. (2.18) формуласынан
қуатты өсіру үшін ![]() шамасын
— қуат коэффициентін ұлғайту қажет
екенін көреміз. Өндірістік қондырғыларда
ең аз дегенде
шамасын
— қуат коэффициентін ұлғайту қажет
екенін көреміз. Өндірістік қондырғыларда
ең аз дегенде ![]() болуы
керек.
болуы
керек.
33.Символдық әдіс. Комплекстік кедергі. Комплекстік түрдегі Ом заңы.
Символдық әдіс: Синусоидалы тоқ тізбегін есептеу үшін символдық әдіс те қолданылады.
Символдық әдіс вектормен жүргізілетін геометриялық іс-әрекетті алгебралыққа ауыстыруға мүмкіндік береді. Сондай-ақ айнымалы тоқ тізбегін есептеуді тұрақты тоқ тізбегін есептейтін әдіспен жүргіземіз.
Символдық әдіс былай жүргізіледі:
а)
әрбір
 вектор тік бұрыш координат жүйесі
өсінде
вектор тік бұрыш координат жүйесі
өсінде
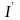 және
және
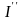 құраушыларға жіктеледі (6.3 –сурет);
құраушыларға жіктеледі (6.3 –сурет);
б)
абсцисса өсін нақты
мәндер өсі
деп атайды және «+», «–» таңбаларымен
белгіленеді. Ордината өсін жорамал
мәндер өсі
деп атайды. Жорамал өстегі вектор
құраушысын
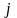 ерекше символымен белгілейді. Сондықтан
бұл әдіс символдық деп аталады.
ерекше символымен белгілейді. Сондықтан
бұл әдіс символдық деп аталады.
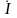 векторы мынаған тең:
векторы мынаған тең:
в)
әрбір векторды
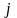 символына көбейту осы векторды сағат
тілінің жүрісіне қарама-қарсы 900
– қа бұрады.
символына көбейту осы векторды сағат
тілінің жүрісіне қарама-қарсы 900
– қа бұрады.
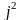 - қа көбейту векторды 1800
– қа бұрады, яғни
- қа көбейту векторды 1800
– қа бұрады, яғни
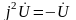 ,
осыдан г) вектор комплексті шама сияқты
комплексті жазықтықта қарастырылады.
Сондықтан бұл әдісті «комплексті
шамалар әдісі»
деп те атайды.
,
осыдан г) вектор комплексті шама сияқты
комплексті жазықтықта қарастырылады.
Сондықтан бұл әдісті «комплексті
шамалар әдісі»
деп те атайды.
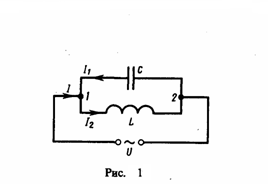
34.Токтардың резонансы
Ток
резонансы
Параллель
жалғанған әртүрлі кедергілерден тұратын
схемадағы резонанс құбылысын
Екінші
тармақтағы ток I2 кернеуге Uab қарағанда
Оны
келесі түрде жазуға болады.
Тізбектің
тармақталмаған бөлігіндегі ток
;
Анықтама
бойынша кіре берістегі ток I кернеумен
U
Демек,
схемадағы резонанс режимінің пайда
болуы шарт былай
.
ω,
L, C-ны немесе R1, R2 өзгерту арқылы
Егер
R1 мен R2, ρ-дан
екеуі де үлкен
кезінде
және R1<<ρ,
R2<<ρ
кезінде резонанс жиілігі
резонанс
жиілігі , яғни резонанс кез
Тағы
айта кететін бір жағдай мынада, формулаға
бес
Жиілік
сипаттамалары
Параллель
жалғанған R, L, C тербелмелі контурына
зерттеулер
Резонанс
сипаттамалылығы дегеніміз, ол активтік
кедергідегі, индуктивтік кедергідегі,
Мұндағы
IC берілген генератор тогы. Q-параллель
контурдың сапалылығы.
Бірізді
контур үшін
.
Параллель
контурдағы резонанс
Екі
тармақты параллельді тізбекті
қарастырайық: біреуінің параметрлері
–
1-сурет
Мұндай
тізбекті көбінесе параллельді контур
деп атайды. Резонанс
реактивті
құраушысы
(1)
және
тармақтың
реактивті өткізгіштері.
b2
= -b1 болғанда фаза бойынша қарама-қарсы
тоқтардың
Тізбектің
параметрі және жиілігі арқылы көрсетілген
b1 және
(2)
(w,
L, C, r1, r2) мөлшерлерінің бәреуін
өзгертумен
w-ға
байланысты теңдеуді шешіп, резонанстың
бұрыштық жиілігінің келесі
(3)5.14
Егер
r1 және r2 кедергілері ρ-ден
үлкен не
r1
= r2 ≠ ρ
болғанда резонанс жиілігі
r1
= r2 = ρ
болғанда резонанс жиілігі
Рассмотрим
цепь переменного тока, которая содержит
параллельно включенные катушку
индуктивностью L и конденсатор емкостью
С (рис. 1). Сделаем допущение для простоты,
что активное сопротивление обеих ветвей
настолько мало, что им можно пренебречь.
Если приложенное напряжение изменяется
по закону U= Umсosωt
, то (см. предудущий раздел формулу (11))
в ветви цепи 1С2 течет ток ![]()
амплитуда
которого (см. предудущий раздел формулу
(10)) при условии R=0 и L=0: ![]()
Начальная
фаза φ1 этого
тока (см. предудущий раздел формулу
(9)) ![]() (1)
(1)
Аналогично,
сила тока в ветви цепи 1L2 ![]()
амплитуда
которого находится из формулы (10)
предыдущего раздела при условии R=0 и
С=∞ : ![]()
Начальная
фаза φ2 этого
тока ![]() (2)
(2)
Из
сравнения выражений (1) и (2) следует, что
разность фаз токов в ветвях 1С2 н 1L2 равна
φ1-φ2 =
π, т. е. токи в ветвях являются
противоположными по фазе. Амплитуда
силы тока во внешней (неразветвленной)
цепи ![]()
Если ![]() ,
то
,
то ![]() и
и ![]() .
Явление резкого уменьшения амплитуды
силы тока во внешней цепи, которая
питает параллельно включенные конденсатор
и катушку индуктивности, при приближении
частоты ω приложенного напряжения к
резонансной частоте ωrez называется резонансом
токов (параллельным
резонансом).
В данном случае для резонансной частоты
получили такое же значение, как и при
резонансе напряжений (см. предыдущий
раздел).
.
Явление резкого уменьшения амплитуды
силы тока во внешней цепи, которая
питает параллельно включенные конденсатор
и катушку индуктивности, при приближении
частоты ω приложенного напряжения к
резонансной частоте ωrez называется резонансом
токов (параллельным
резонансом).
В данном случае для резонансной частоты
получили такое же значение, как и при
резонансе напряжений (см. предыдущий
раздел).
Амплитуда
силы тока Im оказалась
равна нулю, поскольку активным
сопротивлением контура пренебрегли.
Если сопротивление R не равно нулю, то
разность фаз φ1-φ2 будет
равна π, поэтому при резонансе токов
амплитуда силы тока Im будет
не равна нулю, но примет наименьшее
возможное значение. Значит, при резонансе
токов во внешней цепи токи I1 и
I2 компенсируются
и сила тока I в подводящих проводах
достигает минимального значения,
который обусловлен только током через
резистор. При резонансе токов силы
токов I1 и
I2 могут
быть значительно больше силы тока
I.
Рассмотренный
здесь контур оказывает большое
сопротивление переменному току с
частотой, которая близка по значению
к резонансной. Поэтому это свойство
резонанса токов применяется в резонансных
усилителях, которые позволяют выделять
одно определенное колебание из сигнала
сложной формы. Более того, резонанс
токов применяется в индукционных печах,
где нагревание металлов производится
вихревыми токами. В них емкость
конденсатора, который включен параллельно
нагревательной катушке, подбирается
таким образом, чтобы при частоте
генератора получился резонанс токов,
в результате чего сила тока через
нагревательную катушку будет гораздо
больше, чем сила тока в подводящих
проводах.