Проверка статистических гипотез.

О.Ю. Ермолаев «Математическая статистика для психологов». Глава 5 «Общие принципы проверки статистических гипотез»

Н.Ш. Кремер «Теория вероятностей и математическая статистика». Глава 10 «Проверка статистических гипотез»

1. 
   С помощью критерия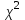 проверьте гипотезу о нормальном распределении 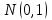генеральной совокупности задачи №1 из зачетного задания №2 (задача о 100 числах, уровень значимости 0,05).
   

Замечание. Образец решения задачи можно посмотреть в книге Н.Ш. Кремер «Теория вероятностей и математическая статистика» стр.373.

2. 
   Повторить эксперимент на стр. 127, задача 8.1.(О.Ю. Ермолаев «Математическая статистика для психологов»). Для составления таблицы кубик подбросить 120 раз. Проверить гипотезу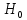 об отсутствии различий в теоретическом и эмпирическом распределениях.
   
3. 
   Даны результаты контрольной работы по математике студентов двух групп 3 курса
   

№ п/п	Первая группа	Вторая группа
	4	16
	7	15
	0	11
	11	12
	4	6
	1	13
	3	20
	7	11
	1	2
	7	13
	7	10
	7	17
	4	20
	10	14
	4	8
	4	18
	2	12
	5	13
	3	10
	1	-
	11	-

---

Ознакомьтесь с гдавой 9. (стр 169) учебника (О.Ю. Ермолаев «Математическая статистика для психологов»). Рассмотрите примеры 9.1 (стр.170) и 9.3 (стр.175). Необходимо сравнить результаты работ в группах, опираясь на эти примеры, используя t-критерий Стьюдента и F-критерий Фишера, сформулировать соответствующие критериям гипотезы, проверить их, сформулировать вывод.

4. 
   Из глав 6 – 9 (О.Ю. Ермолаев «Математическая статистика для психологов») выберите другой пример, который, на ваш взгляд, мог бы быть вам полезен при проверке статистических гипотез в курсовых исследованиях, ВКР и т.п. – занесите его в лист ответа и спрогнозируйте результаты какого эксперимента, соответствующего вашим интересам, он мог бы помочь обработать.
   

1. 
   
   

Таблица 1. Значения функции Ф(x) =

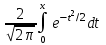
Целые и десятые доли х	Сотые доли х
	0	1	2	3	4	5	6	7	8	9
0,0	0,0000	0,0080	0,0160	0,0239	0,0319	0,0399	0,0478	0,0558	0,0638	0,0717
0,1	0,0797	0,0876	0,0955	0,1034	0,1113	0,1192	0,1271	0,1350	0,1428	0,1507
0,2	0,1585	0,1663	0,1741	0,1819	0,1897	0,1974	0,2051	0,2128	0,2205	0,2282
0,3	0,2358	0,2434	0,2510	0,2586	0,2661	0,2737	0,2812	0,2886	0,2960	0,3035
0,4	0,3108	0,3182	0,3255	0,3328	0,3401	0,3473	0,3545	0,3616	0,3688	0,3759
0,5	0,3829	0,3899	0,3969	0,4039	0,4108	0,4177	0,4245	0,4313	0,4381	0,4448
0,6	0,4515	0,4581	0,4647	0,4713	0,4778	0,4843	0,4907	0,4971	0,5035	0,5098
0,7	0,5161	0,5223	0,5285	0,5346	0,5407	0,5467	0,5527	0,5587	0,5646	0,5705
0,8	0,5763	0,5821	0,5878	0,5935	0,5991	0,6047	0,6102	0,6157	0,6211	0,6265
0,9	0,6319	0,6372	0,6424	0,6476	0,6528	0,6579	0,6629	0,6679	0,6729	0,6778
1,0	0,6827	0,6875	0,6923	0,6970	0,7017	0,7063	0,7109	0,7154	0,7199	0,7243
1,1	0,7287	0,7330	0,7373	0,7415	0,7457	0,7499	0,7540	0,7580	0,7620	0,7660
1,2	0,7699	0,7737	0,7775	0,7813	0,7850	0,7887	0,7923	0,7959	0,7984	0,8029
1,3	0,8064	0,8098	0,8132	0,8165	0,8198	0,8230	0,8262	0,8293	0,8324	0,8355
1,4	0,8385	0,8415	0,8444	0,8473	0,8501	0,8529	0,8557	0,8584	0,8611	0,8638
1,5	0,8664	0,8690	0,8715	0,8740	0,8764	0,8789	0,8812	0,8836	0,8859	0,8882
1,6	0,8904	0,8926	0,8948	0,8969	0,8990	0,9011	0,9031	0,9051	0,9070	0,9090
1,7	0,9109	0,9127	0,9146	0,9164	0,9181	0,9199	0,9216	0,9233	0,9249	0,9265
1,8	0,9281	0,9297	0,9312	0,9327	0,9342	0,9357	0,9371	0,9385	0,9392	0,9412
1,9	0,9426	0,9439	0,9451	0,9464	0,9476	0,9488	0,9500	0,9512	0,9523	0,9533
2,0	0,9545	0,9556	0,9566	0,9576	0,9586	0,9596	0,9606	0,9616	0,9625	0,9634
2,1	0,9643	0,9651	0,9660	0,9668	0,9676	0,9684	0,9692	0,9700	0,9707	0,9715
2,2	0,9722	0,9729	0,9736	0,9743	0,9749	0,9756	0,9762	0,9768	0,9774	0,9780
2,3	0,9786	0,9791	0,9797	0,9802	0,9807	0,9812	0,9817	0,9822	0,9827	0,9832
2,4	0,9836	0,9841	0,9845	0,9849	0,9853	0,9857	0,9861	0,9865	0,9869	0,9872
2,5	0,9876	0,9879	0,9883	0,9886	0,9889	0,9892	0,9895	0,9898	0,9901	0,9904
2,6	0,9907	0,9910	0,9912	0,9915	0,9917	0,9920	0,9922	0,9924	0,9926	0,9928
2,7	0,9331	0,9933	0,9935	0,9937	0,9939	0,9940	0,9942	0,9944	0,9946	0,9947
2,8	0,9949	0,9951	0,9952	0,9953	0,9955	0,9956	0,9958	0,9959	0,9960	0,9961
2,9	0,9963	0,9964	0,9965	0,9966	0,9967	0,9968	0,9969	0,9970	0,9971	0,9972
3,0	0,9973	0,9974	0,9975	0,9976	0,9976	0,9977	0,9978	0,9979	0,9979	0,9980
3,1	0,9981	0,9981	0,9982	0,9983	0,9983	0,9984	0,9984	0,9985	0,9985	0,9986
3,2	0,9986	0,9987	0,9987	0,9988	0,9988	0,9989	0,9989	0,9989	0,9990	0,9990
3,3	0,9990	0,9991	0,9991	0,9991	0,9992	0,9992	0,9992	0,9992	0,9993	0,9993
3,4	0,9993	0,9994	0,9994	0,9994	0,9994	0,9994	0,9995	0,9995	0,9995	0,9995
3,5	0,9995	0,9996	0,9996	0,9996	0,9996	0,9996	0,9996	0,9996	0,9997	0,9997
3,6	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9998	0,9998	0,9998
3,7	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998
3,8	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999
3,9	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999
4,0	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999

---

---

Таблица 4. Значения 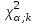критерия Пирсона

Число степеней свобо­ды к	Вероятность α
	0,99	0,98	0,95	0,90	0,80	0,70	0,50	0,30	0,20	0,10	0,05	0,02
1	0,00	0,00	0,00	0,02	0,06	0,15	0,45	1,07	1,64	2,71	3,84	5,41
2	0,02	0,04	0,10	0,21	0,45	0,71	1,39	2,41	3,22	4,60	5,99	7,82
3	0,11	0,18	0,35	0,58	1,00	1,42	2,37	3,66	4,64	6,25	7,82	9,84
4	0,30	0,43	0,71	1,06	1,65	2,20	3,36	4,88	5,99	7,78	9,49	11,7
5	0,55	0,75	1,14	1,61	2,34	3,00	4,35	6,06	7,29	9,24	11,1	13.4
6	0,87	1,13	1,63	2,20	3,07	3,83	5,35	7,23	8,56	10,6	12,6	15,0
7	1,24	1,56	2,17	2,83	3,82	4,67	6,35	8,38	9,80	12,0	14,1	16.6
8	1,65	2,03	2,73	3,49	4,59	5,53	7,34	9,52	11,0	13,4	15,5	18,2
9	2,09	2,53	3,32	4,17	5,38	6,39	8,34	10,7	12,2	14,7	16,9	19,7
10	2,56	3,06	3,94	4,86	6,18	7,27	9,34	11,8	13,4	16,0	18,3	21.2
11	3,05	3,61	4,58	5,58	6,99	8,15	10,3	12,9	14,6	17,3	19,7	22.6
12	3,57	4,18	5,23	6,30	7,81	9,03	11,3	14,0	15,8	18,5	21,0	24,1
13	4,11	4,76	5,89	7,04	8,63	9,93	12,3	15,1	17,0	19,8	22,4	25,5
14	4,66	5,37	6,57	7,79	9,47	10,8	13,3	16,2	18,1	21,1	23,7	26,9
15	5,23	5,98	7,26	8,55	10,3	11,7	14,3	17,3	19,3	22,3	25,0	28,3
16	5,81	6,61	7,96	9,31	11,1	12,6	15,3	18,4	20,5	23,5	26,3	29,6
17	6,41	7,26	8,67	10,1	12,0	13,5	16,3	19,5	21,6	24,8	27,6	31,0
18	7,02	7,91	9,39	10,9	12,9	14,4	17,3	20,6	22,8	26,0	28,9	32.5
19	7,63	8,57	10,1	11,6	13,7	15,3	18,3	21,7	23,9	27,2	30,1	33,7
20	8,26	9,24	10,8	12,4	14,6	16,3	19,3	22,8	25,0	28,4	31,4	35,0
21	8,90	9,92	11,6	13,2	15,4	17,2	20,3	23,9	26,2	29,6	32,7	36,3
22	9,54	10,6	12,3	14,0	16,3	18,1	21,3	24,9	27,3	30,8	33,9	37,7
23	10,2	11,3	13,1	14,8	17,2	19,0	22,3	26,0	28,4	32,0	35,2	39,0
24	10,9	12,0	13,8	15,7	18,1	19,9	23,3	27,1	29,6	33,2	36,4	40,3
25	11,5	12,7	14,6	16,5	18,9	20,9	24,3	28,2	30,7	34,4	37,7	41,7
26	12,2	13,4	15,4	17,3	19,8	21,8	25,3	29,2	31,8	35,6	38,9	42,9
27	12,9	14,1	16,1	18,1	20,7	22,7	26,3	30,3	32,9	36,7	40,1	44,1
28	13,6	14,8	16,9	18,9	21,6	23,6	27,3	31,4	34,0	37,9	41,3	45,4
29	14,3	15,6	17,7	19,8	22,5	24,6	28,3	32,5	35,1	39,1	42,6	46,7
30	14,9	16,3	18,5	20,6	23,4	25,5	29,3	33,5	36,2	40,3	43,8	48,0

---

---

Смотрите также файлы

• 4. Задан тезис Это государство не является ни федерацией, ни конфедерацией.docx

• Экзаменационные вопросы по курсу инфекционных болезней.pdf

• Юридический факт как предпосылка возникновения и функционирования правовых отношений.rtf

• Законов Древней Руси назывался 1 Русская правда 2 Соборное уложение.doc

• Отмена крепостного права и Великие реформы 18601870 гг. Закрепощение крестьян в России. Причины и последствия.docx