- последовательнымсоединением называют совокупность элементов, для которой необходимым и достаточным условием нарушения работоспособности является отказ хотя бы одного (любого) элемента, входящего в данную совокупность;

- параллельнымсоединением называется совокупность элементов, работоспособность которой нарушается только при условии отказа всех элементов, входящих в эту совокупность.

Таким образом, тип соединения в структурной схеме определяется влиянием отказов отдельных элементов (или звеньев) на работоспособность системы в целом, т.е. определяется видом и характером отказов составляющих систему элементов.

Пример последовательного соединения элементов показан на рис.1,а. При последовательном соединении элементов вероятность безотказной работы системы за время t при известных вероятностях безотказной работы элементов равна

, (1)

где P₁(t), P₂ (t),…,P_n(t)- вероятности безотказной работы1,2,3,…,n-го элементов системы за времяt;n– число элементов системы.

Если известны законы изменения интенсивностей  отказов элементов системы, то

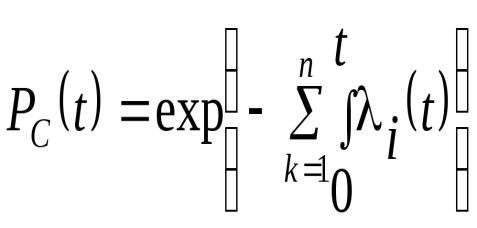. (2)

Расчёт по формуле (1) может выполняться только для момента времени t, для которого известны вероятностиP_i(t), а по формуле (2) для любого времени непрерывной работы системы.



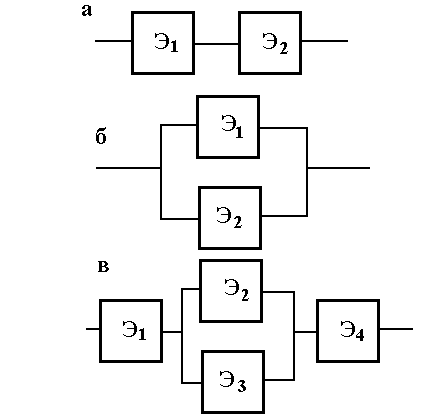
Рис.1. Структурные схемы соединения элементов:

а - последовательное; б - параллельное; в - последовательно-параллельное (смешанное)

При допущении о независимости отказов элементов интенсивность отказов системы равна сумме интенсивностей отказов отдельных элементов

. (3)

Наработка до отказа системы при последовательном соединении элементов равна наработке до отказа того элемента, у которого эта наработка минимальна

---

Т_с = min(T_i),i = 1,2,…,n, гдеn– число элементов системы.

Вероятность отказа системы, состоящей из последовательно соединённых элементов, определяется по формуле

. (4)

При параллельном соединении элементов (рис.1,б) отказ системы возникает только в том случае, когда откажут все её элементы. Вероятность отказа системы за время t при параллельном соединении элементов системы определяется зависимостью

Q_c(t) = q₁(t)q₂(t)…q_n(t) , (5)

где q₁(t) ,q₂(t), q₃(t),…,q_n(t) - вероятности отказов1,2,3,…,n-го элементов системы за времяt; n– число элементов системы.

Вероятность безотказной работы для этого случая (при условии, что система и каждый элемент системы рассматриваются только в одном из двух состояний – работоспособном и неработоспособном)

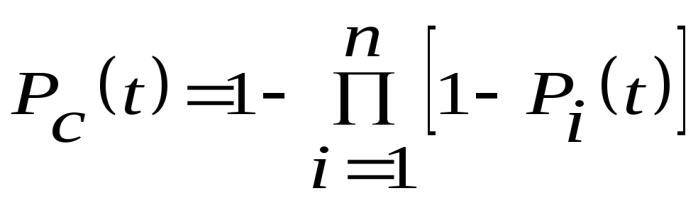. (6)

Вероятность безотказной работы при равнонадёжных элементах и показательном распределении наработки до отказа

, (7)

где - интенсивность отказа одного элемента.

Наработка на отказ системы при параллельном соединении элементов равна максимальному из значений наработок до отказа элементов

T_c = max (T_i) , i = 1,2,…,n.

Если отдельные составные части системы представляют собой параллельное соединение элементов, а другие - последовательное, то рассчитывают вначале вероятности безотказной работы составных частей системы с параллельным соединением элементов, а затем эти составные части соединяют в систему как последовательные элементы (рис.1, в).

Если структурная схема состоит из kпараллельных цепей, а каждая цепь состоит из N звеньев, то вероятность безотказной работы параллельно-последовательной схемы может быть вычислена по уравнению



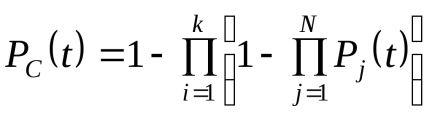
Для частного случая – экспоненциального закона распределения наработок до отказа – расчётные формулы для последовательного и параллельного соединений можно упростить и представить в виде

---

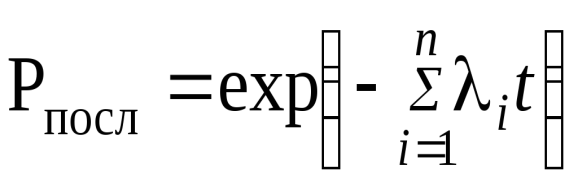
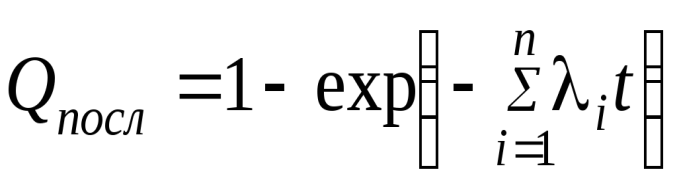. (8)

Для параллельного соединения



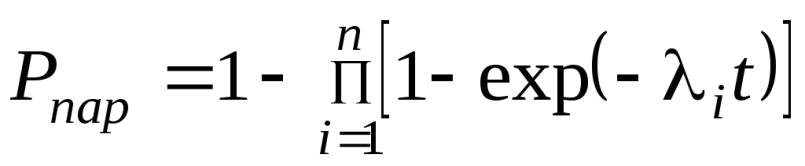
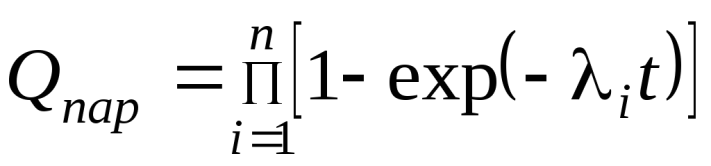. (9)

---

5. Модель безотказности невосстанавливаемых изделий.

Невосстанавливаемым является объект, для которого в рассматриваемой ситуации проведение восстановления работоспособного состояния не предусмотрено в нормативнотехнической, конструкторской документации. Построение модели безотказности состоит из: формирования признаков отказа; выбора и обоснования функции распределения наработки до отказа; определение численных значений параметров функции надежности по статистическим данным, полученным по испытаниям и в процессе наблюдения при эксплуатации; На основании составленной модели возможен расчет любых показателей надежности. При формировании модели надежности восстанавливаемого объекта дополнительно нужно строить модель восстанавливаемости, в которой должны быть формализованы процессы обнаружения, локализации отказов, наладки и предпусковой подготовки.

Модель функционирования невосстанавливаемых изделий представлена на рис. 114. Крестик в кружке обозначает отказ, обозначение осей то же, что и у модели восстанавливаемых изделий. Как видим, данная модель значительно проще. В момент некоторой наработки   деталь либо отказала и невосстанавливалась, либо работоспособна.



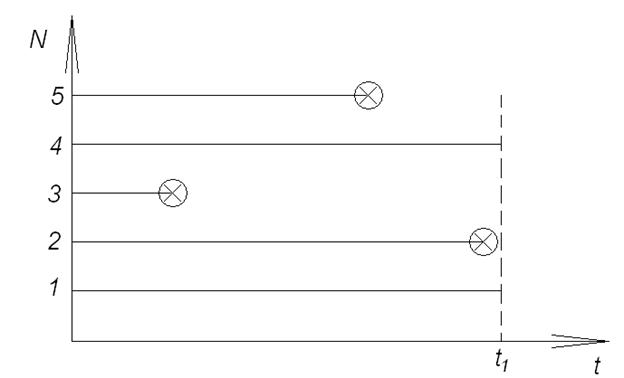
Рис.114. Модель функционирования невосстанавливаемых изделий

7. Расчет надежности функциональных систем методом логических схем ЗК.

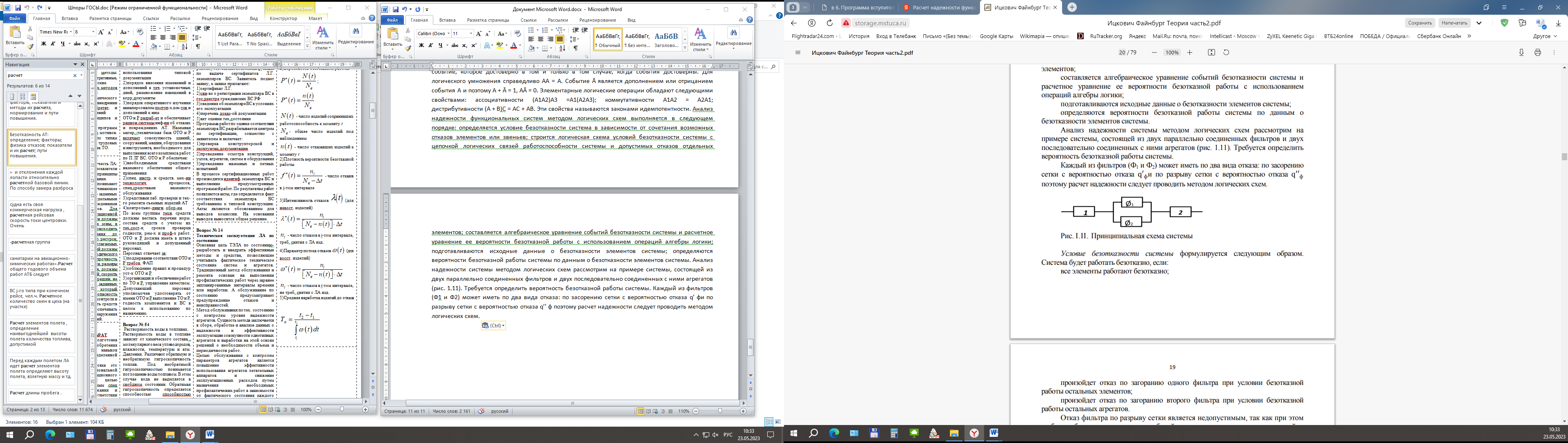
При анализе надежности сложных многофункциональных систем, элементы которых могут иметь несколько видов зависимых отказов, не соблюдаются необходимые условия для применения метода структурных схем (п. 1.2). В этих случаях может использоваться метод логических схем. В логической схеме в отличие от структурной допускается налиие звеньев с зависимыми событиями и повторение звеньев одинакового содержания. Метод логических схем использует операции логического сложения и умножения. Логическое сложение A1 + A2 читается как «A1 или A2». Эта функция выражает событие, которое достоверно в том и только в том случае, если по крайней мере одно из двух событий A1 и A2 является достоверным. Для логического сложения справедливо А + А = А. Логическое умножение A1A2 читается «A1 и A2». Эта функция выражает событие, которое достоверно в том и только в том случае, когда события достоверны. Для логического умножения справедливо АА = А. Событие Ā является дополнением или отрицанием события А и поэтому А + Ā = 1, АĀ = 0. Элементарные логические операции обладают следующими свойствами: ассоциативности (A1A2)A3 =A1(A2A3); коммутативности A1A2 = A2A1; дистрибутивности (А + В)С = АС + АВ. Эти свойства называются законами идемпотентности. Анализ надежности функциональных систем методом логических схем выполняется в следующем порядке: определяется условие безотказности система в зависимости от сочетания возможных отказов элементов или звеньев; строится логическая схема условий безотказности системы с цепочкой логических связей работоспособности системы и допустимых отказов отдельных элементов; составляется алгебраическое уравнение событий безотказности системы и расчетное уравнение ее вероятности безотказной работы с использованием операций алгебры логики; подготавливаются исходные данные о безотказности элементов системы; определяются вероятности безотказной работы системы по данным о безотказности элементов системы. Анализ надежности системы методом логических схем рассмотрим на примере системы, состоящей из двух параллельно соединенных фильтров и двух последовательно соединенных с ними агрегатов (рис. 1.11). Требуется определить вероятность безотказной работы системы. Каждый из фильтров (Ф1 и Ф2) может иметь по два вида отказа: по засорению сетки с вероятностью отказа q′ фи по разрыву сетки с вероятностью отказа q′′ ф поэтому расчет надежности следует проводить методом логических схем.

---

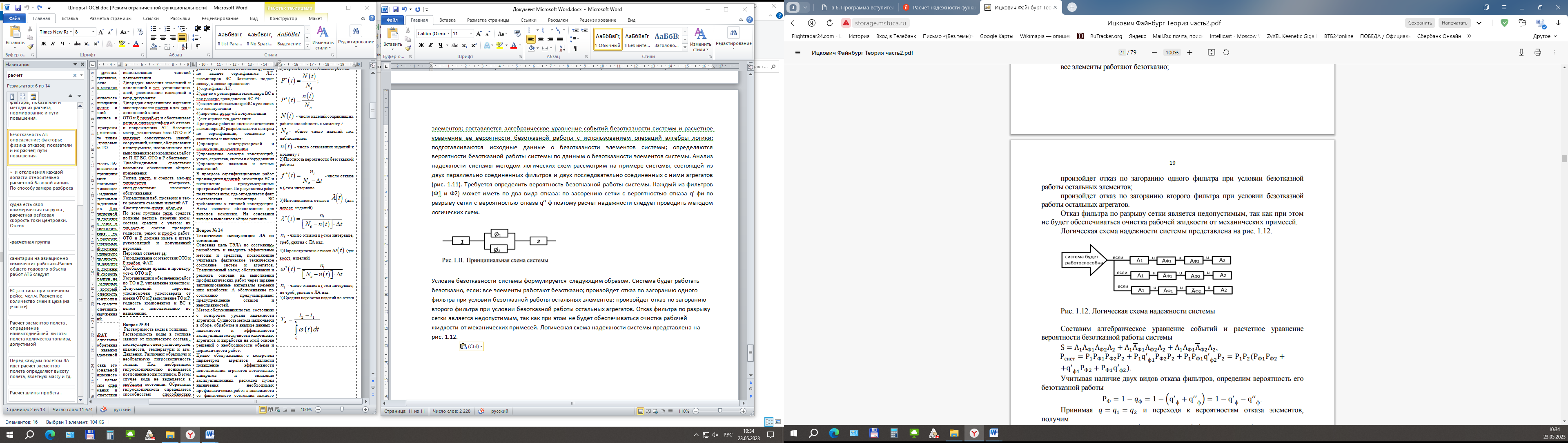
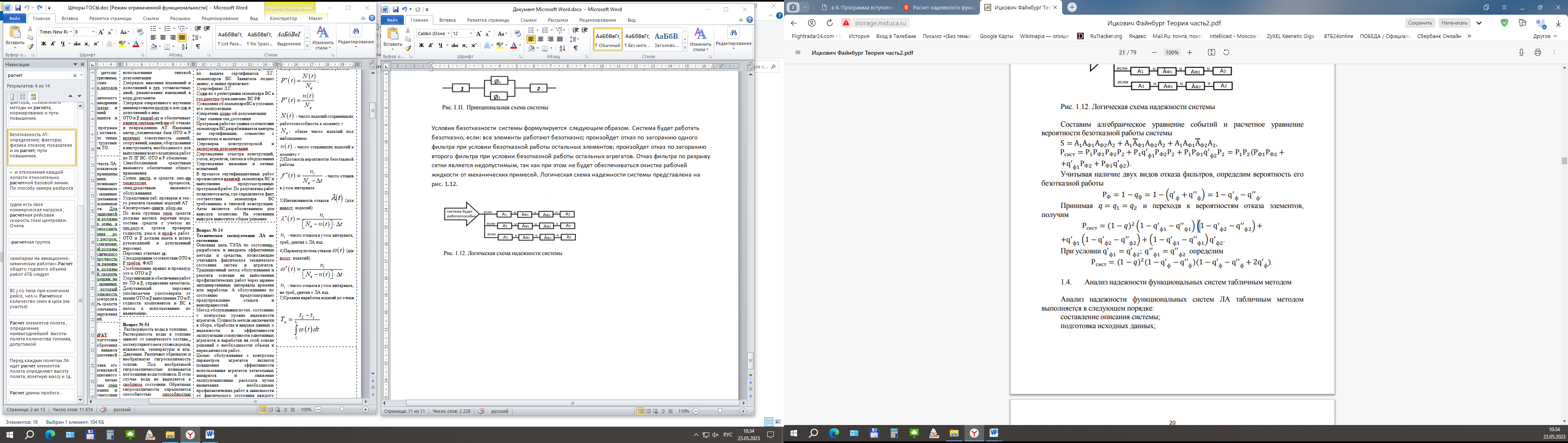
Условие безотказности системы формулируется следующим образом. Система будет работать безотказно, если: все элементы работают безотказно; произойдет отказ по загоранию одного фильтра при условии безотказной работы остальных элементов; произойдет отказ по загоранию второго фильтра при условии безотказной работы остальных агрегатов. Отказ фильтра по разрыву сетки является недопустимым, так как при этом не будет обеспечиваться очистка рабочей жидкости от механических примесей. Логическая схема надежности системы представлена на рис. 1.12.





Вопросы 4 раздела.

1. Прогрессивные технологические процесса ремонта авиационной техники: плазменные методы восстановления; лазерные технологии; методы с использованием эффекта памяти формы; вакуумные методы. Восстановление на основе моделирования процессов пайки.

Плазма – частично или полностью ионизированный газ, в котором концентрация «+» и «-» зарядов практически равна между катодом (чистый вольфрам или с добавлением 2% тория) и медным, охлажденным водой соплом, служащим анодом, возникает дуга нагревающая поступающий в сопло горелки газ, который истекает из сопла в виде плазменной струи. В качестве рабочего газа используют аргон или азот, к которым иногда добавляется водород. Порошковый наплавочный материал подается в сопло струей транспортирующего газа, нагревается плазмой и с ускорением переносится на поверхность основного материала для образования покрытия. Для восстановления изношенных поверхностей плазмен­ным напылением широкое применение получили самофлюсующиеся сплавы системы Ni-Cr-B-Si, в которые нередко добавляют карбиды, бориды тугоплавких металлов (вольфрама, молибдена, ванадия) для образования композиционных сплавов с более вы­сокими физико-химическими свойствами. Весьма эффективно использование биметал­лических терм о реагирующих порошковых сплавов (например, Al + Ni), обладающих экзотермическими свойствами, повышающими прочность сцепления покрытия с осно­вой и физико-химические свойства в целом. Их применяют в качестве подслоя или для напыления основного слоя.

---

Смотрите также файлы

• 1 Туристские ресурсы как основа для организации туристской деятельности в регионе 8.docx

• Викторина Тема игрывикторины Космос Цель работы на основе знаний о развитии космоса, создать интерактивную игру для своих друзей.docx

• Программа учебной практики включает в себя следующее изучение профессиональных стандартов должности проектного менеджера.pdf

• 2) Что такое локальный экстремум Покажите это на основе решения (5%). f(x)extr f(x) 4x 2456, x.docx

• Б по роду тока и принципу действия.pptx