Файл: Оптимизация.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 08.11.2023

Просмотров: 146

Скачиваний: 10

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Письменная работа «Оптимизация»

Вариант №1.

1. Провестирасчетсетевогографика втабличнойи графическойформе. Рассчитать резервывремениработ.Определитькоэффициентынапряженности3-хпутей(повыбору).Таблица 1. Исходные данные

Код

работы
tij,

нед.
Ранние сроки
Поздние сроки
Rп
rсв

tij

рн
tij

ро
tij

пн
tij

по

1-2
2
0
2
0
2
0
0

1-3
2
0
2
4
6
4
4

1-4
4
0
4
8
12
8
8

2-3
4
2
6
2
6
0
0

2-5
3
2
5
19
22
17
3

3-4
6
6
12
6
12
0
0

3-5
2
6
8
20
22
14
0

4-6
6
12
18
12
18
0
0

5-7
4
8
12
22
26
14
14

6-7
8
18
26
18
26
0
0
Решение.

  1. Строим рабочий сетевой график (рис.1)
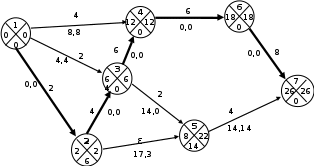
Рисунок 1. Расчетный сетевой графикКритический путь: (1,2)(2,3)(3,4)(4,6)(6,7)Продолжительность критического пути: 262. Рассчитываем временные характеристики сетевого графика непосредственно на графике.2.1. Определение ранних сроков наступления событий tp(i).Ранний срок tp(i) свершения i-ого события определяется продолжительностью максимального пути, предшествующего этому событию: tp(i) = max(t(Lni) (1) где Lni – любой путь, предшествующий i-ому событию, то есть путь от исходного до i-ого события сети.Если событие j имеет несколько предшествующих путей, а следовательно, несколько предшествующих событий i, то ранний срок свершения события j удобно находить по формуле:tp(j) = max[tp(i) + t(i,j)] (2)Если в событие входит одна стрелка (например, событие (2), то к раннему сроку наступления предыдущего события 0 прибавляется продолжительность работы 1-2 (2), tp(2) равно 2.В событие 5 входит две работы: 2-5 и 3-5. Поэтому вначале получаем два значения: 2 + 3 =5, 6+2=8. Большее значение (8 нед.) является ранним сроком наступления события 5 (tp(5) равно 8 нед.).Продвигаясь далее последовательно по работам от исходного события к завершающему, определяем, что tp(7) =26 дней. Поскольку завершающее событие всегда лежит на критическом пути, можно сказать, что 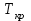= tp(7) = 26 нед. Через какие работы и события пройдет критический путь, мы не знаем, но его продолжительность уже определена при расчете первого параметра сети.2.2. Определение поздних сроков наступления событий tп(i).Поздний срок tп(i) свершения i-ого события равен:tп(i) = tkp - max(t(Lci)) (3)где Lci - любой путь, следующий за i-ым событием, т.е. путь от i-ого до завершающего события сети.Если событие i имеет несколько последующих путей, а, следовательно, несколько последующих событий j, то поздний срок свершения события i удобно находить по формуле:tп(i) = min[tп(j) - t(i,j)] (4)Расчет ведется от завершающего события

(с конца графика) в строго обратном порядке. Поскольку у событий, лежащих на критическом пути, ранние и поздние сроки совпадают, то для завершающего события tп(7) = tp(7) = 26 нед.

Для остальных событий в соответствии с формулой (3) можно рассчитать следующим образом. Для события 6 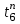= 26-8 = 18 нед, для события 5 – 26-4=22 нед.

Продвигаясь далее последовательно к исходному событию, получаем 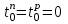. Такой результат является критерием правильности расчетов ранних и поздних сроков наступления событий и может использоваться для самопроверки.

3.3. Определение резервов времени событий .

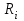Расчет можно вести или с начала графика, или с его конца. Для любого события . , .

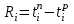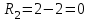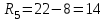Значение рассчитанных параметров событий заносим в таблицу 2.
Таблица 2

Расчетные параметры событий



Номер события
Сроки свершения события:

Резерв времени, R(i)

ранний tp(i)
поздний tп(i)

1
0
0
0

2
2
2
0

3
6
6
0

4
12
12
0

5
8
22
14

6
18
18
0

7
26
26
0
3.4. Расчет параметров работ табличным методом (таблица 3). Перечень работ и их продолжительность перенесем в первую и вторую графы. При этом работы записываем в графу 1 последовательно: сначала начиная с номера 1, затем с номера 2 и т.д.Графу 3 (tp(i)) и графу 6 получаем из таблицы 2 (tп(j)).Значения в графе 4 получаются в результате суммирования граф 2 и 3.В графе 5 позднее начало работы определяется как разность позднего окончания этих работ и их продолжительности (из значений графы 6 вычитаются данные графы 2);Содержимое графы 7 (полный резерв времени RП(ij)) равно разности граф 5 и 3 или граф 6 и 4. Если RП(ij) равен нулю, то работа лежит на критическом пути.Таблица 3Расчет параметров сетевой модели по времени

Работа (i,j)
Продолжительность tij
Ранние сроки: начала tijР.Н.
Ранние сроки: окончания tijР.О.
Поздние сроки: начала tijП.Н.
Поздние сроки: окончания tijП.О.
Резерв времени: полный RijП
Свободный резерв, RijC

1
2
3
4
5
6
7
8

(1,2)
2
0
2
0
2
0
0

(1,3)
2
0
2
4
6
4
4

(1,4)
4
0
4
8
12
8
8

(2,3)
4
2
6
2
6
0
0

(2,5)
3
2
5
19
22
17
3

(3,4)
6
6
12
6
12
0
0

(3,5)
2
6
8
20
22
14
0

(4,6)
6
12
18
12
18
0
0

(5,7)
4
8
12
22
26
14
14

(6,7)
8
18
26
18
26
0
0
Свободный резерв времени RС работы (i,j) представляет собой часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события. Rc находится по формуле:RС(i,j)= Rп(i,j) - R(j) (5)Значение свободного резерва времени работы указывает на наличие резервов, необходимых для оптимизации.Критический путь: (1,2)(2,3)(3,4)(4,6)(6,7)Продолжительность критического пути: 26.Определяемкоэффициентынапряженности3-хпутей (Kн).Путь L1: 1-2-5-7. L1=2+3+4=9. Кн=L1/Lкр=9/26=0,346.Путь L2: 1-4-6-7. L1=4+6+8=9. Кн=L2/Lкр =18/26=0,692.Путь L3: 1-3-5-7. L1=2+2+4=8. Кн=L3/Lкр =8/26=0,308.

Смотрите также файлы