Х	Y
	1	3
	3	5
	2	3
	5	4
	2	3
	5	6
	6	7
	2	2
	3	3
	6	8
	4	6
	1	2
	3	4
	4	4
	6	8
	5	6
	1	1
	4	5

Лабораторная работа по пакету STATISTICA

1.

Таблица данных
Задания:

Внести данные в пакет Statistica
2. Расчет основных статистик
Для подсчета основных числовых характеристик щелкните по кнопке «Статистика». На рис.6 она указана стрелкой.

---

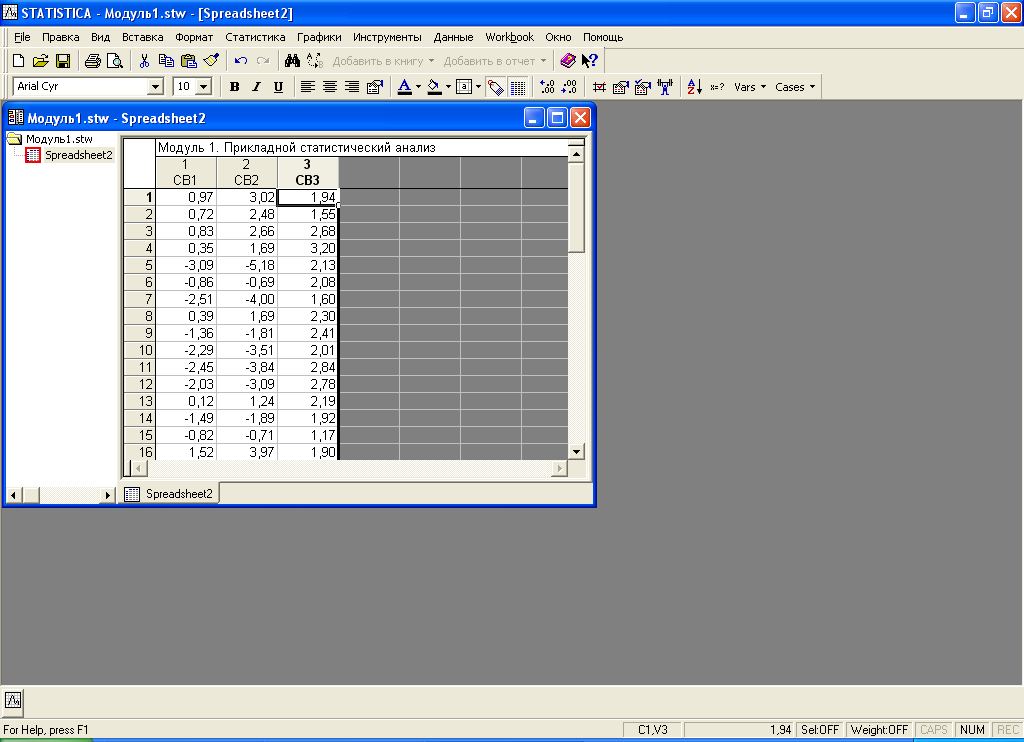
Рис.6. Диалоговое окно перед началом статистической обработки
В результате появится диалоговое окно, представленное на рис.7.


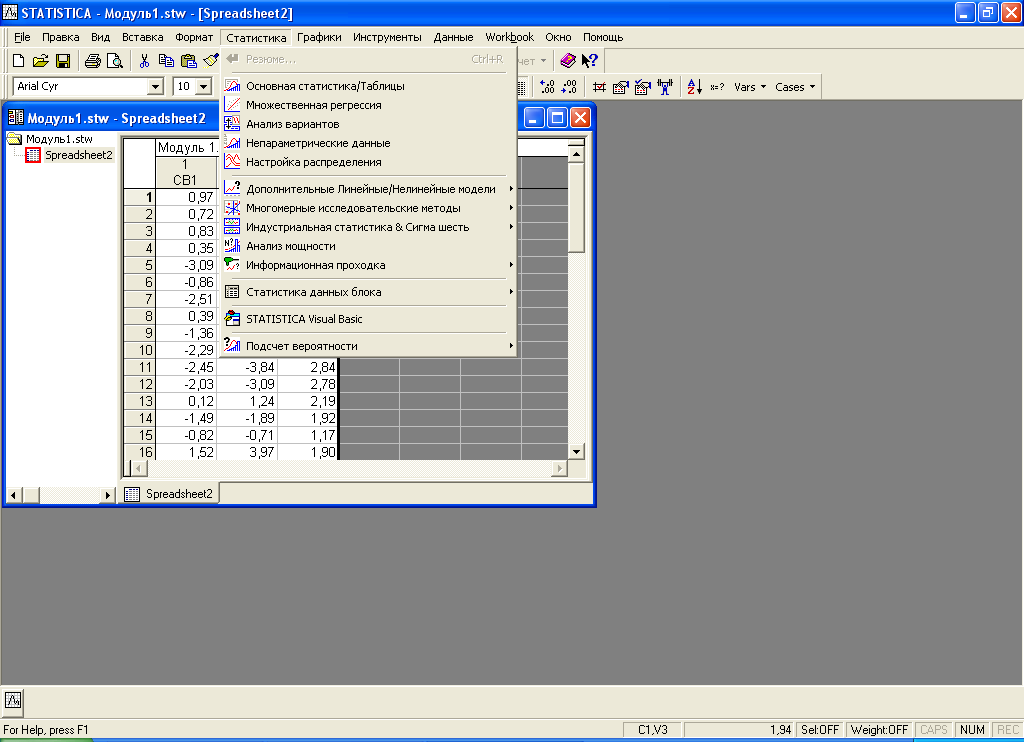
Рис.7. Окно выбора разделов статистической обработки
Щелкнем по кнопке, указанной стрелкой. Появится диалоговое окно, представленное на рис.8.



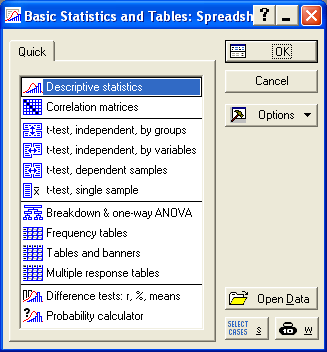
Рис.8. Окно для выбора методов обработки исходной таблицы

Выберем курсором нужный раздел обработки. В нашем случае раздел указан стрелкой «Descriptive statistics» - описательная статистика и щелкнем по кнопке «ОК». В результате появится окно, представленное на рис.9.



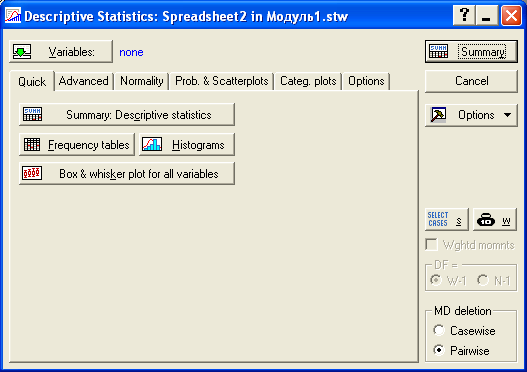
Рис.9. Диалоговое окно для выбора режимов обработки
Здесь кнопка «Variables:» - переменные, предназначена для выбора столбцов из основной таблицы, для которых будет производиться обработка. При щелчке по этой кнопке появится окно, представленное на рис.10.



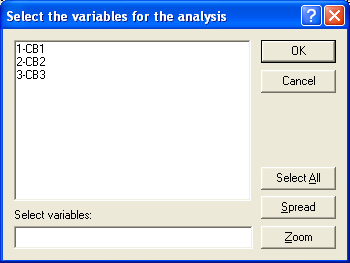
Рис.10. Диалоговое окно для «селекции» переменных
Можно выделить либо одну какую-то переменную, активизировав её щелчком курсора, либо несколько переменных. При этом для выбора переменных необходимо удерживать клавишу «Ctrl» на клавиатуре. Если обработку необходимо проводить для всех переменных, можно щелкнуть по кнопке «Select All». После выбора переменных необходимо нажать на кнопку «ОК».

Затем вновь появиться диалоговое окно рис.9. Щелкнем по кнопке «Advanced» - расширенный. Появится диалоговое окно, представленное на рис.11.


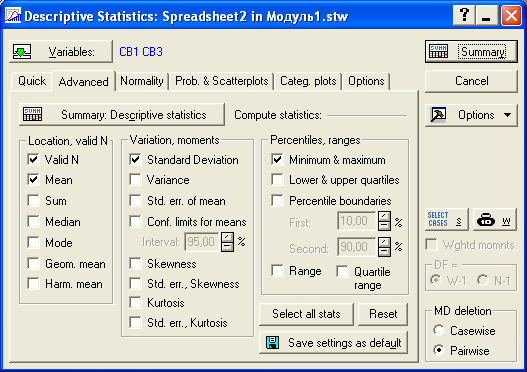
Рис. 11. Диалоговое окно для выбора необходимых числовых характеристик
Здесь

в первой левой колонке представлены:
Valid N - объем выборки;

Ниже приведены точечные оценки.

---

Mean – математическое ожидание;

Sum - сумма вариант;

Median – медиана;

Mode – мода;

Geom. mean – среднее геометрическое;

Harm. Mean – среднее гармоническое;
во второй колонке представлены:
Standard Deviation - среднеквадратичное отклонение;

Variance - дисперсия;

Std. err. mean - стандартная ошибка математического ожидания;

Conf. limits for means – концы доверительного интервала для математического ожидания;

Skewness - асимметрия;

Std. err.Skewness - стандартная ошибка асимметрии;

Kurtosis - эксцесс;

Std. err.Kurtosis - стандартная ошибка эксцесса;
во третьей колонке представлены:
Minimum & maximum – максимальная и минимальная варианты;

Lower& upper quartiles - нижний и верхний квартили;

Percentile boundaries - границы процентилей;

Range - размах варианты;

Quartile range - размах квартиля.
Отметив галочками необходимые числовые характеристики, щелкнем по кнопке «Summary» - вычислить.

Например, в нашем случае были выбраны характеристики, представленные на рис.12.

После того, как будет нажата кнопка «Summary», произойдет расчет отмеченных характеристики и результаты появятся в окне, представленном на рис.13 и 14. Если все результаты не помещаются в окне, используются полосы прокрутки, как вертикальные, так и горизонтальные. На рис.13. стрелкой указана вертикальная полоса прокрутки.




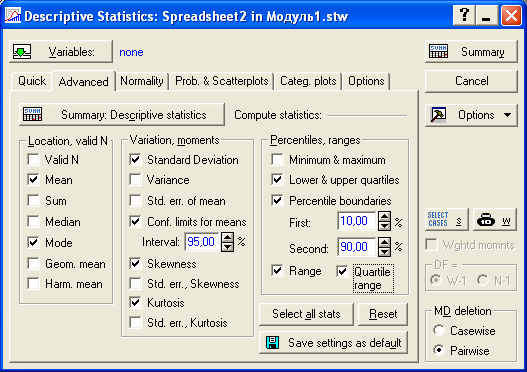
Рис.12. Галочками отмечены числовые характеристики, которые будут вычисляться

В отчет внести: результаты по х и по у:

Valid N - объем выборки;

Mean – математическое ожидание;

Sum - сумма вариант;

Median – медиана;

Mode – мода;

Standard Deviation - среднеквадратичное отклонение;

Variance - дисперсия;
3. Коробка - усы
Статистика / основная статистика / t-test / Ok

В результате появиться диалоговое окно, представленное на рис.19.


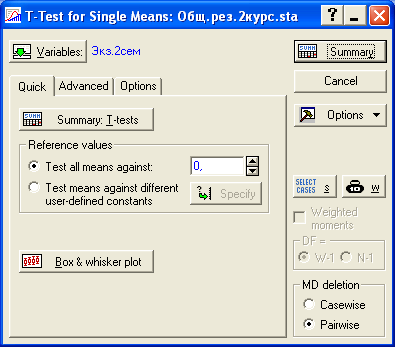
Рис.19. Диалоговое окно для построения диаграмм «коробка-усы»
Как обычно, нажав на кнопку «Variables:», выбирают необходимые переменные, для которых необходимо построить диаграмму «коробка-усы». Затем щелкнув по кнопке «

---

Box whisker plot», вызывают диалоговое окно, представленное на рис. 20.


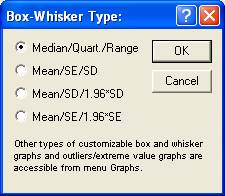
Рис.20. Диалоговое окно для выбора форм диаграмм

Здесь
Median/Quar./Range - внутренний квадратик соответствует Me[X], сторона прямоугольника (коробки) равна интервалу, куда попадают 50% значений СВ. Внешний отрезок соответствует размаху значений СВ, т.е. .
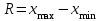Mean/SE/SD - внутренний квадратик соответствует M[X], сторона прямоугольника (коробки) равна стандартной ошибке для математического ожидания. Внешний отрезок соответствует значению среднего квадратического отклонения.
Mean/SD/1.96*SD - внутренний квадратик соответствует M[X], сторона прямоугольника (коробки) равна среднему квадратическому отклонению. Внешний отрезок соответствует значению среднего квадратического отклонения, умноженному на 1.96.
Mean/SE/1.96*SE - внутренний квадратик соответствует M[X], сторона прямоугольника (коробки) равна стандартной ошибке для математического ожидания. Внешний отрезок соответствует значению стандартной ошибке для математического ожидания, умноженному на 1.96.
В отчет по Х и по Y скриншот графика,

внимательно рассмотреть появившийся график и провести описательный анализ данных по представленному ниже шаблону.

Первый график относится к Х: нижняя риска находится на значении ___, верхняя на значении ___. Это минимальное и максимальное значение.. Медиана равна ___

. 4. Корреляционный анализ

Путь: Статистика / основная статистика / Correlations matrices / ok

В результате появиться диалоговое окно вида


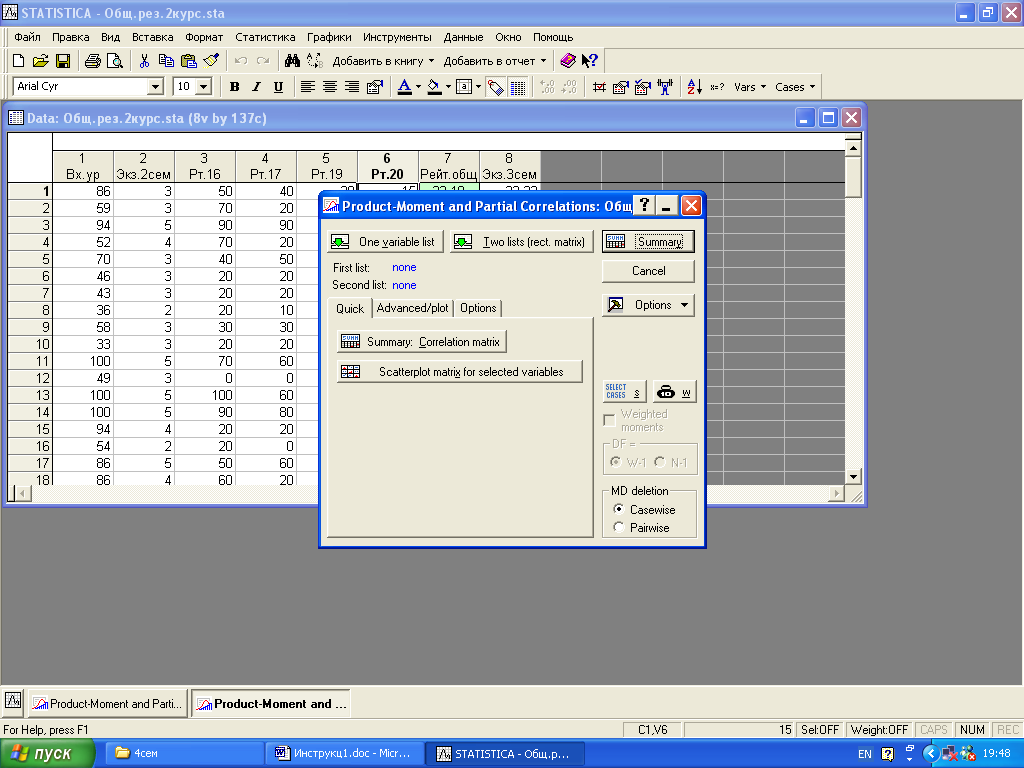
Рис.28. Окно для выбора режимов корреляционного анализа
Нажмем на клавишу One variable list (список переменных),

Выбрав переменные, необходимо нажать кнопку ОК . В результате появиться окно, представленное на рис.30.

---

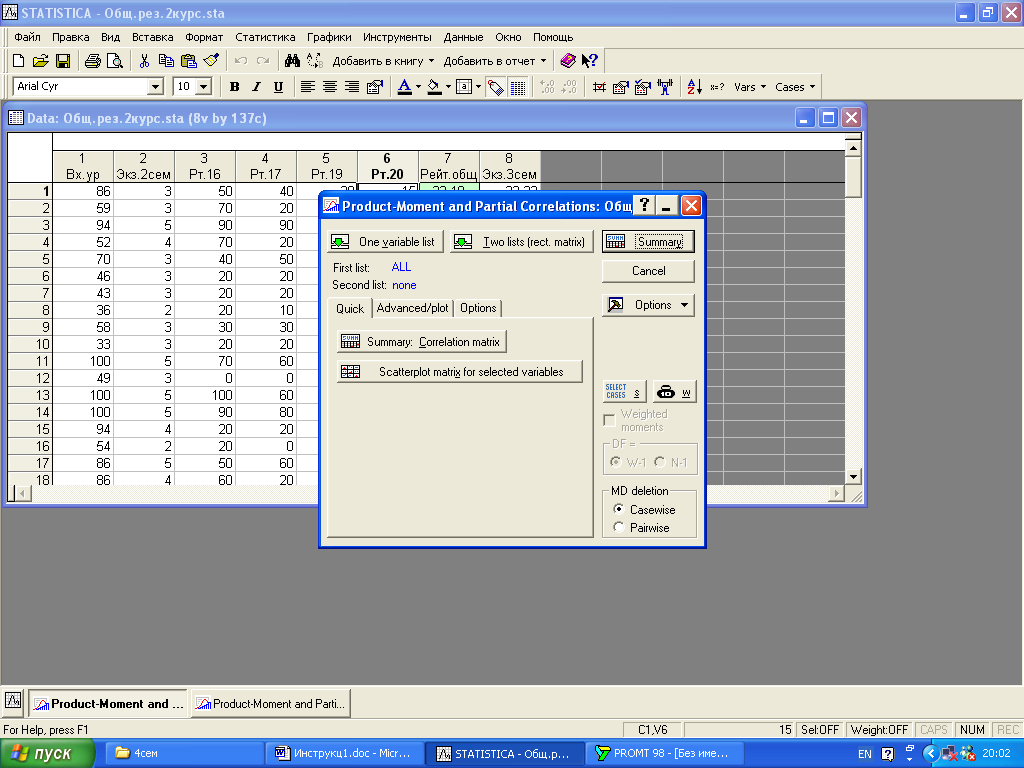
Рис.30. Окно для выбора вариантов обработки

Если выбрать режим 2D scatter plot (двумерное корреляционное поле), нажав на клавишу 2D scatter plot, то появиться окно, позволяющее выбрать какие-то две переменные, для которых необходимо построить корреляционное поле. В нашем случае выбраны первая и вторая переменные. Причем, из этих двух переменных одну можно считать «первой» - аргументом (First variable), а другую «второй» - функцией (Second variable). Нажав на ОК, получим результат, представленный на рис.34.




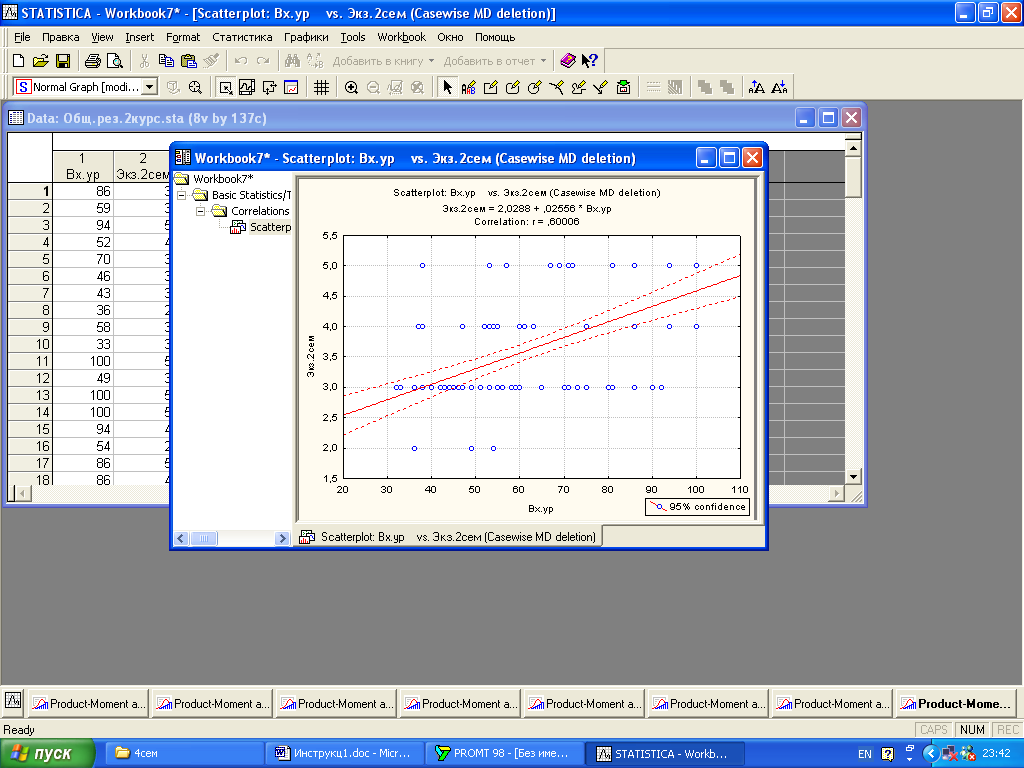
Рис.34. Корреляционное поле для первой и второй переменной с указанием уравнения регрессии, графика уравнения регрессии и доверительной «полосы» при 0.95 доверительной вероятности (по умолчанию), с указанием коэффициента парной корреляции
В отчет: значение коэффициента корреляции
5. Регрессионный анализ
Уравнение регрессии от одной переменной
Линейная регрессия (без проверки гипотезы на адекватность)

Путь: графики / графики рассеивания / переменные / дополнительно / тип графика/ подгонка / ОК
После нажатия кнопки «графики рассеивания» появиться диалоговое окно вида



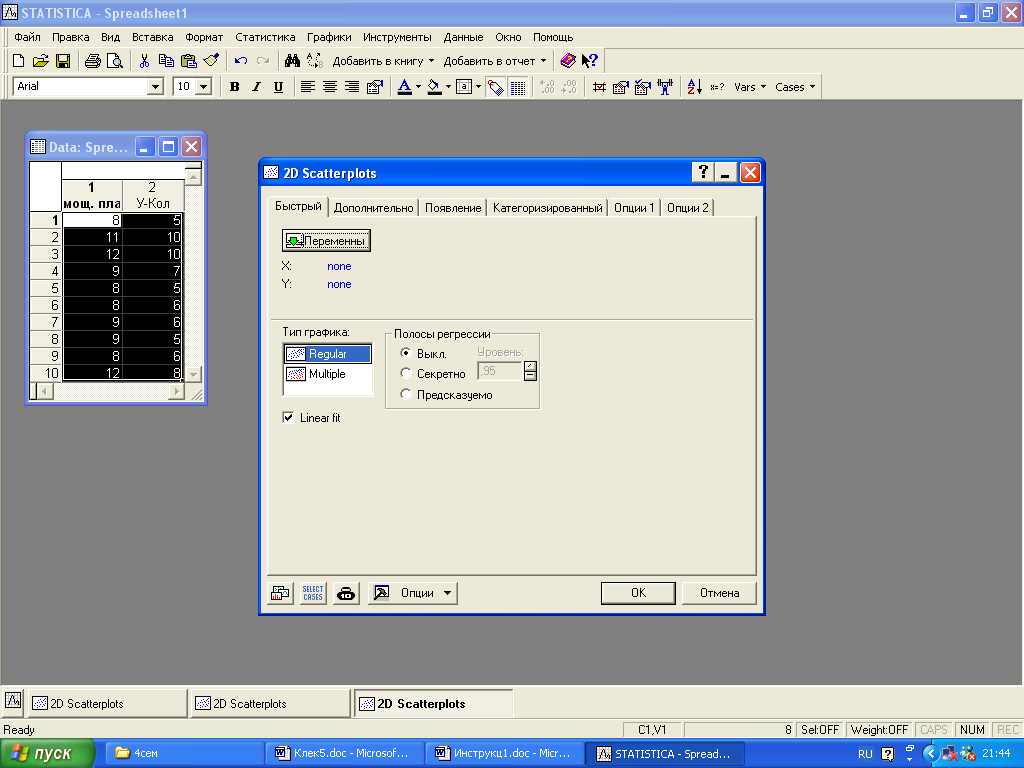
Рис.37. Выбор аргумента и функции
После выбора аргумента и функции (в нашем случае аргумент Х, функция У) и нажатия кнопки «Дополнительно», появится


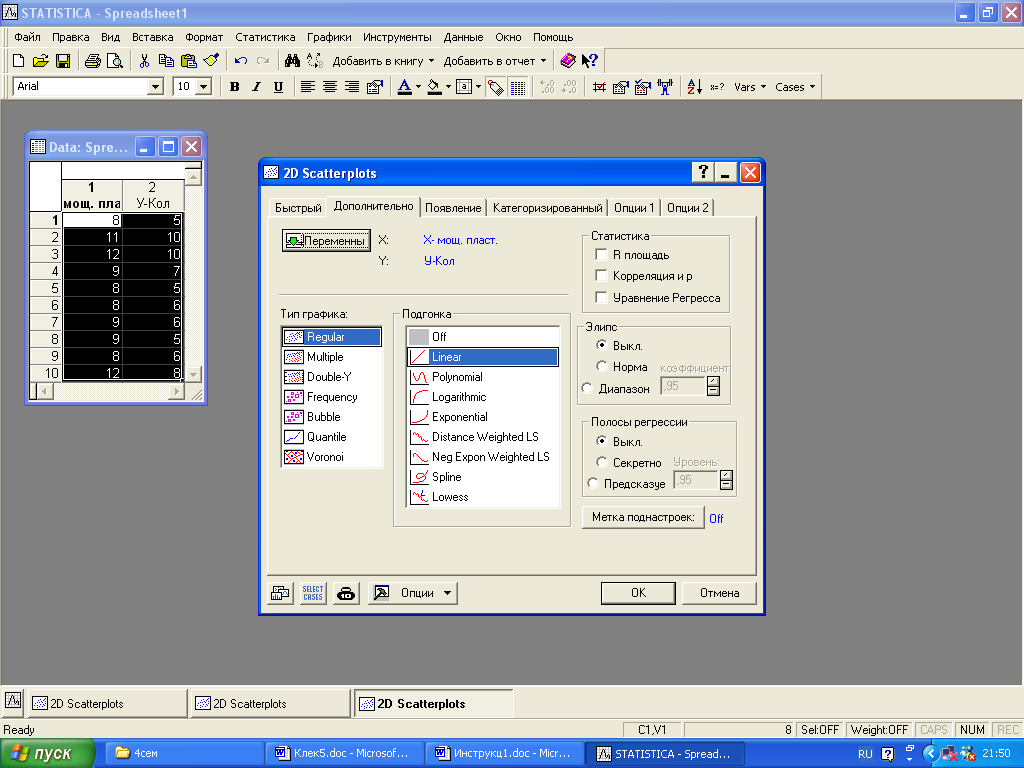
Рис.38. Выбор типа графика (одна функция или несколько); статистика; полосы регрессии (доверительная полоса)
Здесь

тип графика:

Regular – график одной функции,
Multiple – графики нескольких функций (если есть их значения),

Double - Y – изображение оси ОУ справа,

Frequency – частотность(частота),

Quintile – квантиль,
Подгонка:

- вид функциональной зависимости.

Статистика:

- вывод на графике значения коэффициента детерминации, корреляции, уравнения регрессии.

Эллипс:

- вывод на графике эллипса рассеивания при различной доверительной вероятности.

---

Смотрите также файлы

• Программа среднего профессионального образования 38. 02. 01 Экономика и бухгалтерский учет (по отраслям) Дисциплина Выполнение работ по профессии "кассир" Практическое задание 1.doc

• Если принять, то уравнение изоклины для заданного уравнения или уравнение гипербол. Для примера ограничимся значениями, и.doc

• Определение права. Соотношение права и морали, права и обычаи (традиции).docx

• 1. Мышление понятие, классификация. 3 Структура мыслительного процесса. 8.docx

• На день рождения куклы Алины, пришли разные зверята.docx