Файл: Экзамены это не просто "отбарабанил" и ушёл (или "провалился и привет до следующего захода").docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 18
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ» |
| Кафедра экономики и управления Форма обучения: заочная |
ВЫПОЛНЕНИЕ
ПРАКТИЧЕСКИХ ЗАДАНИЙ
ПО ДИСЦИПЛИНЕ
ОСНОВЫ ИНФОРМАЦИОННОЙ КУЛЬТУРЫ И ИНФОРМАТИКА
Группа Уз20Э361
Студент
Ж.М Касимов
МОСКВА 2023 г.
ПСИХОЛОГИЧЕСКАЯ ПОДГОТОВКА К СДАЧЕ ЭКЗАМЕНОВ
Все мы знаем, что экзамен - лотерея. И все ошибаемся. Иначе почему одни всё время выигрывают, а другие, увы, никогда? На самом деле всё проще. Экзамены - не просто отчёт об усвоении некой суммы знаний по какому-то предмету или кругу вопросов. Это и не просто экзекуция, которую нужно (порой - неизбежно нужно!) претерпеть ради получения оценки не ниже определённой (сами знания тут могут быть уже и ни при чём). Нет, экзамены при всём при том, что вышесказанное в них наличествует, - это ещё и технология, и даже тайны, порой очень маленькие, но неизменно очень значительные и, несомненно, важные. Экзамены - это не просто "отбарабанил" и ушёл (или "провалился - и привет до следующего захода"). Это - процесс многокомпонентный и сложный, где каждая из составляющих в какай-то мере незаменима другой, а подчас и просто незаменима. Как же преодолеть этот путь - от начала изучения какого-либо предмета до оценки результатов изучения (и пойти далее, ведь если всерьёз, то финиша на этом пути не бывает)? Оглянитесь вокруг - и вы увидите, что экзамены, то есть, в строгом переводе с латыни, испытания ждут вас на каждом шагу. Ведь что ни говори, но в основной своей части жизнь состоит из вопросов и ответов. В процессе обучения и последующем отчёте о его результатах большую роль играет, во-первых, знание или, точнее, понимание того, что надо делать, и во-вторых, умение это делать, то есть ясное представление о том, как лучше всего реализовать желаемое или необходимое. Или наоборот. При обучении художника или певца его в первую очередь учат технологии или, как говорят, ремеслу, то есть тому, как, например, рисовать, и лишь потом, но уже скорее в его личном плане встаёт проблема, что рисовать. А если перед нами будущий водитель личного автомобиля? Здесь эти процессы оказываются перевёрнуты, инвертированы: сначала он учится вождению (как это делать?) и лишь затем тому, что рациональней со своей машиной делать - пойти ли в магазин пешком или "обуть ноги в колёса". При обучении танцора, например, на каком-то этапе эти процессы могут протекать параллельно, в тесной взаимосвязи.
М
ежду тем при подготовке к экзамену именно второй компонент - как это делать, в том числе и то, как полученные знания использовать на практике, - игнорируются. Это, однако, было бы столь же странно, как если бы будущий ремонтник компьютеров, скажем, изучал лишь схемы, то есть изображение радиокомпонентов на бумаге, так ни разу и не увидев "живьём" ни компьютеров, ни резисторов, ни микросхем, ни даже самих компьютеров, наконец. Но это, так сказать, при взгляде на проблему на макроуровне, то есть на проблему обучения целиком, а если речь идёт о конкретном экзамене?Увы, многие студенты, да и школьники, естественно, упорно "задалбливают" материал, старательно зазубривают всё на тему, которую им предстоит сдавать, нисколько не придавая значения тому, как они это будут делать. В итоге, уже проснувшись утром перед экзаменом (если поспать вообще удалось), они уже обнаруживают в себе сначала лёгкий, но всё возрастающий "мандраж" - и чрезмерное волнение как бы стирает в памяти материал, освоенный, казалось бы, "от" и "до". Да, хорошее знание предмета необходимо для успеха, но это знание нужно ведь ещё и продемонстрировать, причём именно тогда, когда нужно. "Неспокойное волнение" в ситуации экзамена, сколько это ни печально, может быть ещё большим врагом, чем не самое блестящее знание предмета. По данным психолога О. Кондраша, примерно у 23% студентов излишнее волнение самым неприятным, а иногда и фатальным образом влияло на результат экзамена. У абитуриентов, как правило, дела обстоят "ещё веселее". Преподаватели же обычно объясняют провал на экзамене низким уровнем знаний сдающего. И, бывает, ошибаются, так что и преподавателям, выходит, было бы невредно познакомиться с этим материалом. Ведь причиной запредельного волнения сдающего являются порою именно они. Впрочем, если своё волнение можно умерить, то почему нельзя повлиять и на экзаменатора? Можно, но это - если умеючи.
КОГДА ИДТИ ОТВЕЧАТЬ?
Итак, вы пришли на экзамен. Когда зайти в аудиторию - решайте сами. К концу дня экзаменаторы, как правило, менее внимательны, утомлены и не хотят слушать долгие рассуждения. Они чаще останавливают абитуриентов, если хотят поставить "отлично", задают меньше дополнительных вопросов. В это время легче отвечать - при существенных пробелах в знании предмета. Но и оценки к концу дня, как правило ниже. Дело в том, что здесь часто срабатывает преподавательский стереотип - "сильные идут первыми". Мы знаем много примеров, когда абитуриент, всем своим видом демонстрируя, что он отличник, шёл в первой пятёрке - и получал "отлично", его знания были намного скромнее. Поэтому, если вы чувствуете, что знаете чуть больше, чем на "четыре", идите в первой пятёрке и получайте свои пять баллов.
И, наконец, самый крайний вариант - идти отвечать последним. Обычно его используют те, кому нужна тройка. Этот вариант даёт возможность остаться один на один с экзаменатором и сообщить ему дополнительную информацию о себе (трудности в подготовке, большая любовь к предмету, тяжелое детство и т.д.). Однако, если вам не нужна тройка, ни в коем случае не идите последним! Срабатывает упомянутый стереотип - и вы получите оценку ниже своих возможностей. Конечно, не всем попадается экзаменатор, твёрдо уверенный, что последний абитуриент - "двоечник". Но нам известно немало таких случаев. Вот один из них. Абитуриент, поступающий в университет, твёрдо решил идти отвечать последним. Он очень боялся экзамена, хотя имел знания, значительно превышающие уровень, необходимый для тройки. Товарищи его, знавшие предмет гораздо скромнее, пошли в середине группы - и получили свои тройки и четвёрки. Он зашёл последним и не выходил из аудитории полтора часа. О том, что там происходило, ожидавшие его друзья делали самые различные предположения, начиная от партии в шахматы и заканчивая утверждением, что "они там заснули". Наконец абитуриент вышел - и вид его был красноречивей любой оценки. Оказывается, преподаватель был твёрдо убеждён, что последним идёт сдавать экзамен самый закоренелый двоечник. Он полтора часа доказывал это нашему герою. И доказал… Идти отвечать в конце группы нежелательно ещё и потому, что долгое многочасовое ожидание утомит вас. В группах, ожидающие сдачи экзамена, постоянно поддерживается напряженность, которая нередко разряжается в виде острых и юмористических замечаний, в том числе и в ваш адрес. Чем больше вы будете ждать, тем больше тратите энергии на разрядку.
Оптимальный вариант - идти четвертым-пятым в первой пятёрке: у вас будет достаточно времени на подготовку (сорок-пятьдесят минут, пока будет отвечать первые три-четыре человека). Это, впрочем, если и не знают, то чувствуют многие абитуриенты или студенты, и желающих пойти первыми, как правило, более чем
достаточно.
П
оэтому
приходите к входу в учебный корпус, где будете сдавать экзамен, пораньше. Расположение неизвестной вам аудитории полезно бывает выяснить заранее
Задание для практической работы по теме 3
MS Excel
Вариант 1
Задача 1.
По облигации номиналом 50 000 руб., выпущенной на 6 лет, предусмотрен следующий порядок начисления процентов: в первый год – 10%, в следующие два года – 20%, в оставшиеся три года – 25%.
Определить будущую стоимость облигации с учетом переменной процентной ставки.
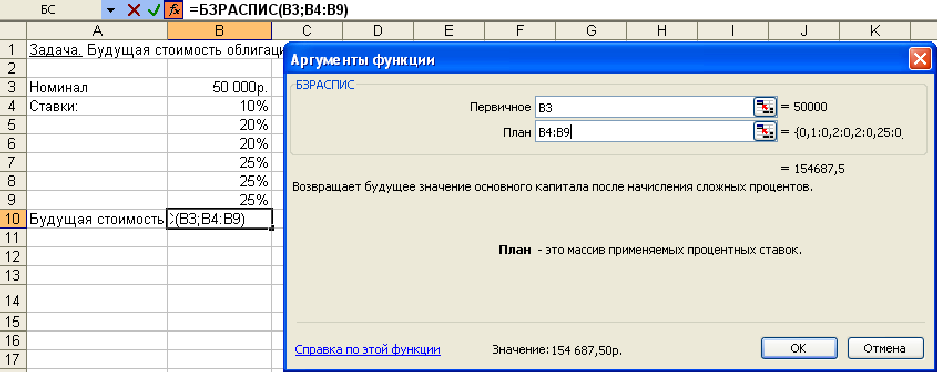
Результат решения задачи – 154 687,50 р. может быть найден и при явной записи функции БЗРАСПИС. Массив процентных ставок в этом случае следует ввести в фигурных скобках:
=БЗРАСПИС(50 000; {0,1; 0,2; 0,2; 0,25; 0,25; 0,25}) = 154687,50
БЗРАСПИС=50000*(1+0,1)*(1+0,2)*(1+0,2)*…= 154687,50
Задача 2.
На банковский счет под 11,5% годовых внесли 37000 руб.
Определить размер вклада по истечении 3 лет, если проценты начисляются каждые полгода.
Алгоритм решения задачи.
Создать рабочую книгу с именем Финансовые функции. Построить таблицу согласно рисунку 1 на отдельном листе.
Поскольку необходимо рассчитать единую сумму вклада на основе постоянной процентной ставки, то используем функцию БС.
Опишем способы задания аргументов данной функции.
В связи с тем, что проценты начисляются каждые полгода, аргумент ставка равен 11,5%/2.
Общее число периодов начисления равно 3*2 (аргумент кпер).
Если решать данную задачу с точки зрения вкладчика, то аргумент пс (начальная стоимость вклада) равный 37 000 руб., задается в виде отрицательной величины (- 37 000), поскольку для вкладчика это отток его денежных средств (вложение средств).
Если рассматривать решение данной задачи с точки зрения банка, то данный аргумент (пс) должен быть задан в виде положительной величины, т.к. означает поступление средств в банк.
Аргумент плт отсутствует, т.к. вклад не пополняется.
Аргумент тип равен 0, т.к. в подобных операциях проценты начисляются в конце каждого периода (задается по умолчанию). Тогда к концу 3-го года на банковском счете имеем:
= БС (11,5%/2;3*2;;-37 000) = 51 746,86 руб., с точки зрения вкладчика это доход
,
= БС (11,5%/2;3*2;;37 000) = - 51 746,86 руб., с точки зрения банка это расход, т.е. возврат денег банком вкладчику.
На практике, в зависимости от условий финансовой сделки проценты могут начисляться несколько раз в год, например, ежемесячно, ежеквартально и т.д. В таблице 1 приведены данные для наиболее распространенных методов внутригодового учета процентов.
Таблица 1 - Расчет данных для различных вариантов начисления процентов
| Метод начисления процентов | Общее число периодов начисления процентов | Процентная ставка за период начисления, % |
| Ежегодный | N | K |
| Полугодовой | N*2 | K/2 |
| Квартальный | N*4 | K/4 |
| Месячный | N*12 | K/12 |
| Ежедневный | N*365 | K/365 |
Этот же расчет можно выполнить по формуле:
Подставив в формулу числовые данные, получим:
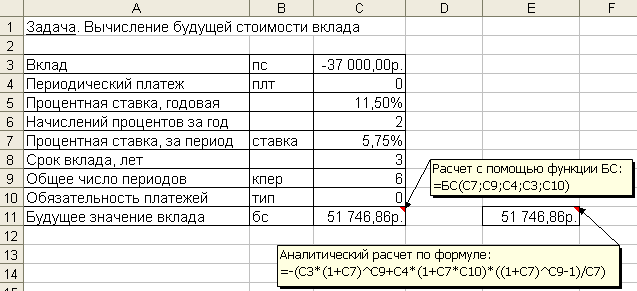
Рисунок 1 - Фрагмент листа Excel с решением задачи о нахождении будущего размера вклада