Файл: Задача 1. Стальной ступенчатый брус нагружен сосредоточенными силами. Соотношение между площадями поперечных сечений приведены на рисунке. Из условия прочности при растяжении найти площадь поперечного сечения А. Определить удлинение стержня.docx
Добавлен: 08.11.2023
Просмотров: 280
Скачиваний: 15
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Раздел №1
Задача №1. Стальной ступенчатый брус нагружен сосредоточенными силами. Соотношение между площадями поперечных сечений приведены на рисунке. Из условия прочности при растяжении найти площадь поперечного сечения А. Определить удлинение стержня.
Дано: вариант №12, схема №2, F1 = 25 кН, F2 = 15 кН, F3 = 55 кН, марка стали Ст4, а = 0,6 м, b = 0,7 м, с = 0,7 м.
Решение:
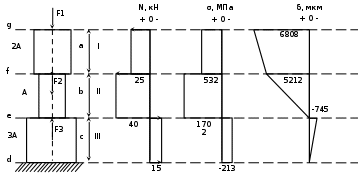
Определим внутренние усилия и напряжения. Пронумеруем участки последовательно от незакрепленного конца. Допускаемое напряжение для стали марки Ст4 согласно справочным данным:
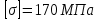. Метод сечений заключается в том, что тело мысленно рассекается плоскостью на две части, любая из которых отбрасывается, а взамен нее к сечению оставшейся части прикладываются внутренние силы, действовавшие до разреза. Оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием внешних и приложенных к сечению внутренних сил.
Согласно третьему закону Ньютона, внутренние силы, действующие в сечении оставшейся и отброшенной частей тела, равны по модулю, но противоположны по направлению. Таким образом, рассматривая равновесие любой из двух частей рассеченного тела, можно получить одно и то же значение внутренних сил, однако выгоднее рассматривать ту часть тела, для которой уравнения равновесия проще.
Итак, воспользовавшись методом сечений и третьим законом Ньютона, определим величины действующих сил.
N1 = F1 = 25 кН
N2 = F1 + F2 = 40 кН
N3 = F1 + F2 – F3 = -15 кН
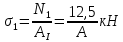
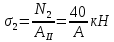
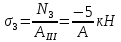
Выполним проверку найденных величин.
Для сечения g:
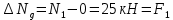
Для сечения f:
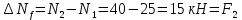
Для сечения e:
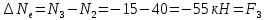
При расчете на прочность по допускаемым напряжениям считается, что прочность обеспечена, если максимальное возникающее в нем напряжение не превышает допускаемого напряжения, поэтому при растяжении условие прочности имеет следующий вид:
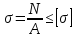
Из условия прочности при растяжении находим требуемое значение площади поперечного сечения А:
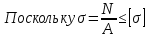, следовательно, 
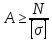, где 
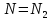, так как участок II является наиболее опасным.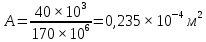
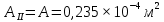
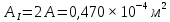
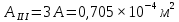
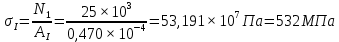
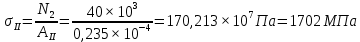
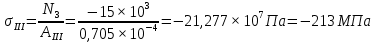
Напряжения деформации при растяжении и сжатии связаны между собой линейной зависимостью, называемой законом Гука. Он гласит – нормальное напряжение прямо пропорционально относительному удлинению или укорочению, то есть:
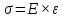
Величина E – коэффициент пропорциональности, характеризующий жесткость материала бруса, то есть его способность сопротивляться деформации. Данный коэффициент называют модулем продольной упругости, модулем упругости первого рода или модулем Юнга. Его значения для различных материалов устанавливаются экспериментально-опытным путем.
Если в формулу закона Гука подставить значения относительного удлинения и напряжения
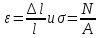, получим следующую зависимость: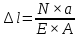
Итак, воспользовавшись законом Гука, определим величину деформации бруса. Величину модуля Юнга E для стали примем равной:
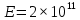Па.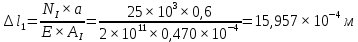
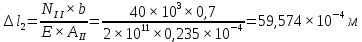
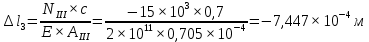
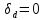
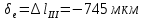
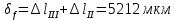
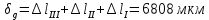
Таким образом, исходя из условия прочности при растяжении, была найдена площадь поперечного сечения наиболее опасного участка ступенчатого бруса, а также площади сечений всех остальных его участков. Также был произведен расчет деформации каждого участка и построена эпюра перемещений сечений. Полная длина бруса в результате воздействия увеличилась на 6,808 мм.
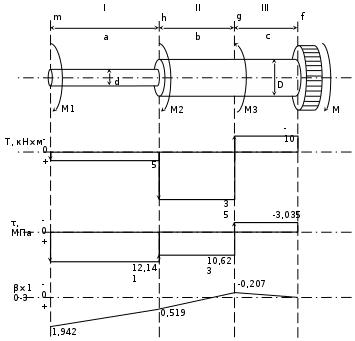
Задача №2. К стальному ступенчатому валу с отношением диаметров D/d = 2 приложены вращающие моменты. Из условия прочности при кручении найти диаметры D и d участков вала. Определить деформацию вала.
Дано: вариант №12, схема №2, M1 = 5 кН×м, M2 = 30 кН×м, M3 = 45 кН×м, марка стали Ст4, а = 0,6 м, b = 0,7 м, с = 0,7 м.
Решение:
Воспользовавшись методом сечений определим внутренние усилия и напряжения. Пронумеруем участки последовательно от незакрепленного конца вала. При этом допускаемое напряжение для стали марки Ст4 согласно справочным данным:
.
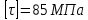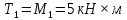
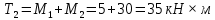
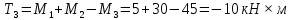
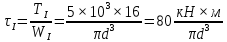
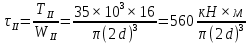
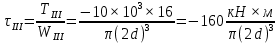
Выполним проверку найденных величин.
Для сечения m:
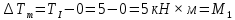
Для сечения h:
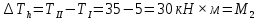
Для сечения g:
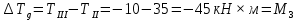
Условие прочности при кручении гласит: прочность вала считается обеспеченной, если наибольшие касательные напряжения, возникающие в его опасном поперечном сечении, не превышают допускаемых напряжений на кручение, то есть:
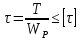, где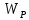 
– момент сопротивления при кручении.Из условия прочности при кручении находим диаметры D и d различных участков вала. Для начала определим величину момента сопротивления
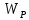.Поскольку
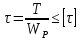, следовательно, 
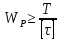, где 
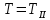, так как участок II является наиболее опасным.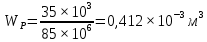
Так как
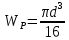, то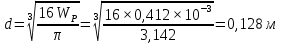 
Таким образом примем значение диаметра d = 128 мм, соответственно диаметр
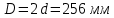
Определим значения напряжений кручения, действующих на участках.
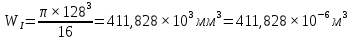
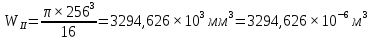
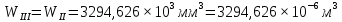
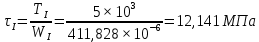
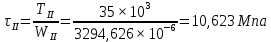
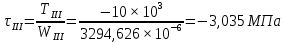
Для вала постоянного поперечного сечения при постоянном по длине l крутящем моменте его абсолютный угол закручивания определяется формулой:
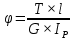
Эта формула описывает закон Гука при кручении, а отношение
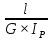носит название крутильной жесткости бруса. Определим с ее помощью деформацию вала. Рассчитаем для каждого из участков угол закручивания, предварительно определив величины полярных моментов инерции.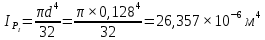
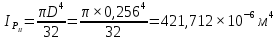
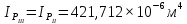
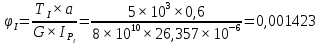
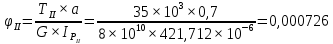
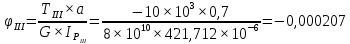
В качестве начала отсчета при построении эпюры перемещения сечения выберем сечение f, для которого
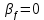
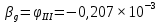
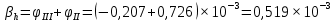
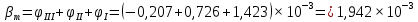
Таким образом, исходя из условия прочности при кручении были найдены диаметры D и d участков ступенчатого вала. Был произведен расчет деформации каждого из участков. При этом незакрепленное сечение вала повернулось относительно точки закрепления на угол 0,001942 радиан.
Список использованных источников
-
Основы расчетов на прочность и жесткость типовых элементов конструкций: учеб. пособие / А.Н. Савкин, В.И. Водпьянов, О.В. Кондратьев, А.А. Седов. – Волгоград: ВолгГТУ, 2019. – 252 c. -
Сопротивление материалов: учебник / Б.Е. Мельников, Л.К. Паршин, А.С. Семенов, В.А. Шерстнев. – СПб.: Лань, 2020. – 576 c. -
Белов, А.А. Нормативно-справочные материалы для прочностных расчетов: метод. указания / А.А. Белов, О. В. Кондратьев, А. С. Столярчук. – Волгоград: ВолгГТУ, 2017. – 16 с.