Определения

Базовыми элементами, которыми оперирует алгебра логики, являются 

• 
  ¬  отрицание (унарная операция),
  
• 
  ∧  конъюнкция (бинарная),
  
• 
  ∨  дизъюнкция (бинарная),
  

Логический ноль 0 и логическая единица 1 — константы.

Также используются названия:

• 
  Дизъю́нкт — пропозициональная формула, являющаяся дизъюнкцией одного или более литералов 
  
• 
  Конъюнкт — пропозициональная формула, являющаяся конъюнкцией одного или более литералов.
  

Логические операции

Простейший и наиболее широко применяемый пример такой алгебраической системы строится с использованием множества B, состоящего всего из двух элементов:

� В = { Ложь, Истина }

Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей, а операции отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ) определяются в привычном нам понимании. Легко показать, что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений и все они могут быть получены через суперпозицию трёх выбранных операций.

Опираясь на этот математический инструментарий, логика высказываний изучает высказывания и предикаты.

Логика высказываний послужила основным математическим инструментом при создании компьютеров. Она легко преобразуется в битовую логику: истинность высказывания обозначается одним битом (0 — ЛОЖЬ, 1 — ИСТИНА); тогда операция ¬и приобретает смысл вычитания из единицы буквальном смысле сложения по модулю 2 (исключающее Или — XOR); ∣

Впоследствии булева алгебра была обобщена от логики высказываний путём введения характерных для логики высказываний аксиом. Это позволило рассматривать, например, логику кубитов, тройственную логику (когда есть три варианта истинности высказывания: «истина», «ложь» и «не определено»), комплексную логику и др.

Приоритет выполнения операций

Для сложных логических выражений, содержащих несколько логических операций, определен порядок выполнения действий (приоритет): сначала операции отрицания, затем операции логического умножения, потом операции логического сложения и исключающего сложения, последними выполняются операции импликации и эквивалентности

---

. Операции выполняются слева направо. Порядок выполнения может быть изменен с помощью скоб.

Пример 1

Определить порядок выполнения логических операций в выражении.

Вычислить его значение, если А = 1, В = 0, С = 1.

¬А ∧ С v (A ⊕ В) ∧ В

Решение. Первыми вычисляются значения в скобках. Затем выполняются операции по приоритетам: самый высокий приоритет имеет операция отрицания, после нее, как в математике, следуют операции умножения, а затем сложения. Таким образом, порядок будет следующий:

Тогда значение выражения ¬1 ∧ 1 v (1 ⊕ 0) ∧ 0 после вычисления отрицания и выражения в скобках: 0 ∧ 1 v 1 ∧ 0, после операций умножения: 0 v 0. Итог: 0.

Ответ: логическое выражение ложно.

Пример 2

Для каких из приведенных слов истинно следующее высказывание?

(Вторая буква гласная) ИЛИ (Первая буква гласная) И НЕ (Длина имени не больше 5 букв)

1) Олег 2) Марианна 3) Светлана 4) Ольга.

Законы математической логики

В алгебре логики имеется ряд законов, позволяющих производить равносильные преобразования логических выражений. Приведем соотношения, отражающие эти законы.

1. 
   Закон двойного отрицания: не (не А) = A.
   

Двойное отрицание исключает отрицание.

2. 
   Переместительный (коммутативный) закон:
   

- для логического сложения: А v B = B v A;

- для логического умножения: A & B = B & A.

Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.

3. 
   Сочетательный (ассоциативный) закон:
   

- для логического сложения: (A v B) v C = A v (B v C);

- для логического умножения: (A & B) & C = A & (B & C).

При одинаковых знаках скобки можно ставить произвольно или вообще опускать.

4. 
   Распределительный (дистрибутивный) закон:
   

- для логического сложения: (A  B) & C = (A & C) (B & C);

- для логического умножения: (A & B) v C = (A v C) & (B v C).

Определяет правило выноса общего высказывания за скобку.

5. 
   Закон общей инверсии (законы де Моргана):
   

- для логического сложения:

---

- для логического умножения:

6. 
   Закон идемпотентности ( от латинских слов idem - тот же самый и potens -сильный; дословно - равносильный):
   

- для логического сложения: A v A = A;

- для логического умножения: A & A = A.

Закон означает отсутствие показателей степени.

7. 
   Законы исключения констант:
   

- для логического сложения: A v 1 = 1, A v 0 = A;

- для логического умножения: A & 1 = A, A & 0 = 0.

8. 
   Закон противоречия: A & (не A)= 0.
   

Невозможно, чтобы противоречащие высказывания были одновременно истинными.

9. 
   Закон исключения третьего: A v (не A) = 1.
   

Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе - ложно, третьего не дано.

10. 
    Закон поглощения:
    

- для логического сложения: A v (A & B) = A;

- для логического умножения: A & (A v B) = A.

11. 
    Закон исключения (склеивания):
    

- для логического сложения: (A & B) v ( & B) = B;

- для логического умножения: (A v B) & (v B) = B.

12. 
    Закон контрапозиции (правило перевертывания):
    

(A B) = (B A).

Справедливость приведенных законов можно доказать табличным способом: выписать все наборы значений А и В, вычислить на них значения левой и правой частей доказываемого выражения и убедиться, что результирующие столбцы совпадут.

Пример. Упростить логическое выражение: 



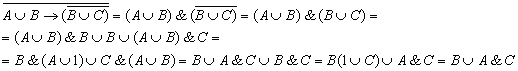
Законы алгебры логики

В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логических выражений:

---

Закон	ИЛИ	И
Переместительный (Коммутативный)	A v B = B v A.	A & B = B & A;
Сочетательный (Ассоциативный)	A v (BvC) = (AvB) v C = A v B v C	A&(B&C) = (A&B)&C = A&B&C;
Распределительный (Дистрибутивный)	A & (B v C) = A&B v A&C	A v (B & C) = (A v B) & (A v C)
Правила де Моргана	(A v B) == A & B	v B
Идемпотенции	A v A == A	A & A == A
Поглощения	A v (B & A) == A	A & (B v A) == A
Склеивания	(A & B) v (A & B) == A	(A v B) & (A v ) == A
Закон противоречия	A & 
Закон исключенного третьего	A v 
Операция с константами	A v 0 = A, A v 1=1	A & 0=0, A&1=1
Двойного отрицания	
Закон тождества	А=А

Если в переместительном и сочетательном законе поменять "&" на знак умножения и "v" на знак сложения, то они превращаются в арифметические формулы перестановки и сочетания.

Рассмотрим некоторые примеры.

По закону тождества А=А каждое высказывание должно быть тождественно самому себе. Зачастую этот закон нарушается преднамеренно. Наиболее распространенным является подмена понятий. Например, в высказывании «Материя бесконечна, но кому-то не хватает на платья», подмена философского понятия материя нетождественным ему понятием материя в смысле ткань (слова омонимы)

1. 
   Закон противоречия A & : два несовместимых высказывания не могут быть одновременно истинными. Например, «Петя участник соревнования» и «Петя не является участником соревнования» ‑ не могут быть одновременно истинными высказываниями.
   
2. 
   Закон исключенного третьего A v  действует по отношению к противоречивым высказываниям: «Либо погода летная, либо не летная».
   

Справедливость любого закона алгебры логики можно доказать разными методами:

• 
  путем прямой подстановки вместо переменной значений 0 и 1(Пример 8 ),
  
• 
  методом перебора всех возможных значений переменных, для которых проверяется справедливость закона, те с помощью таблиц истинности (Пример 9)
  
• 
  с помощью законов алгебры логики (Пример 10 и 11)
  

---

Пример 8. Подставим в закон двойного отрицания значения аргумента:

При А=1 получим 

При А=0 получим 

Пример 9. Докажем с помощью таблицы истинности распределительный закон для логического сложения A v (B & C) = (A v B) & (A v C).

\A	\B	C	B&C	A v B	A v C	Av (B&C)	(A v B)&(A v C)
0	0	0	0	0	0	0	0
0	0	1	0	0	1	0	0
0	1	0	0	1	0	0	0
0	1	1	1	1	1	1	1
1	0	0	0	1	1	1	1
1	0	1	0	1	1	1	1
1	1	0	0	1	1	1	1
1	1	1	1	1	1	1	1

Для доказательства закона достаточно показать тождественность выражений, образующих левую и правую стороны доказываемого соотношения при всех наборах переменных, принимающих значения 0 или 1.

Пример 10. Доказать, что  vv  A&C= A&(В v С)

По закону де Моргана  vА& В, по распределительному закону для сложения получим А& В v  A&C = = A&(В v С)

Отрицание

Отрица́ние (инве́рсия, от лат. inversio — переворот, логи́ческое «НЕ») в логике — унарная операция над суждениями, результатом которой является суждение, «противоположное» исходному. Обозначается знаком ¬ перед или чертой 

---

Смотрите также файлы

• ПСн112подготовка Дата начала тестирования.docx

• Конспект урока английского языка " a family" Дата 31. 01. 2018г. Класс 2 А Раздел Step 30.docx

• Цифровизация новый способ подавления человека.docx

• Программа по курсу Основы духовнонравственной культуры народов России.docx

• Практическая работа 2 по учебному курсу Электроэнергетические системы и сети (наименование учебного курса) Студент.docx