Добавлен: 08.11.2023
Просмотров: 143
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
— над суждением.
Как в классической, так и в интуиционистской логике «двойное отрицание» ¬¬� является следствием суждения �, то есть имеет место тавтология: �→¬¬�
Обратное утверждение ¬¬�→�и верно в классической логике (закон двойного отрицания), но не имеет места в интуиционистской. То есть отрицание отрицания искомого утверждения не может служить интуиционистским доказательством, в отличие от классической логики. Это различие двух логических систем обычно полагается главным.
Схематика
Мнемоническое правило для отрицания звучит так: на выходе будет
Дизъюнкция
Дизъю́нкция (от лат. disjunctio — «разобщение»), логи́ческое сложе́ние, логи́ческое ИЛИ, включа́ющее ИЛИ; иногда просто ИЛИ — логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу».
Дизъюнкция может быть операцией как бинарной (имеющей два операнда), так и � -арной (имеющей � операндов) для произвольного �.
Запись может быть префиксной — знак операции стоит перед операндами (польская запись), инфиксной — знак операции стоит между операндами или постфиксной — знак операции стоит после операндов. При числе операндов более двух префиксная и постфиксная записи экономичнее.
Импликация
Имплика́ция (от лат. implicatio «связь; сплетение») — бинарная логическая связка, по своему применению приближенная к союзам «если…, то…».
Импликация записывается как посылка ⇒ следствие; применяются также стрелки другой формы и направленные в другую сторону, но всегда указывающие на следствие.
Суждение, выражаемое импликацией, выражается также следующими способами:
Импликация играет очень важную роль в умозаключениях. С её помощью формулируются определения различных понятий, теоремы, научные законы.
При учёте смыслового содержания высказываний импликация подразумевает причинную связь между посылкой и заключением.
Конъюнкция
Конъю́нкция (от лат. conjunctio — «союз, связь») — логическая операция, по смыслу максимально приближенная к союзу «и». Синонимы: логи́ческое «И», логи́ческое умноже́ние, иногда просто «И».
Конъюнкция может быть бинарной операцией (т. e. иметь два операнда), тернарной операцией (т. e. иметь три операнда), или n-арной операцией (т. e. иметь n операндов).
Эквиваленция
Логическая равнозначность или эквивале́нция (или эквивале́нтность) — это логическое выражение, которое является истинным тогда, когда оба простых логических выражения имеют одинаковую истинность. Двуместная логическая операция обычно обозначается символом ≡ или ↔.
Эквиваленция �⟺� — это сокращённая запись для выражения (¬�∧¬�)∨(�∧�)
Задаётся следующей таблицей истинности:
Таким образом, высказывание A ≡ B означает «A то же самое, что B», «A эквивалентно B», «A тогда и только тогда, когда B».
Не надо путать эквиваленцию — логическую операцию с логической эквивалентностью высказываний — бинарным отношением. Связь между ними следующая:
Логические выражения � и � эквивалентны в том и только в том случае, когда эквиваленция �⟺� истинна при всех значениях логических переменных.
Заключение
При исследовании данной темы было изучено большое количество теоретических источников, что способствовало систематизации знаний по этой теме. В заключительной части работы я решил применить полученные знания на практике. Тем самым я еще раз подтвердил выдвинутую гипотезу, что математическая логика активно применяется в наше время.
Практическая работа.
1)Установите, какие из следующих предложений являются логическими высказываниями, а какие — нет (объясните почему):
Решение:
2)Укажите, какие из высказываний предыдущего задания истинны, какие — ложны, а какие относятся к числу тех, истинность которых трудно или невозможно установить.
Решение:
3)Составьте таблицы истинности логических выражений:
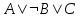
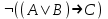
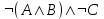
4)Составьте логическую функцию F (X, Y, Z) для заданной таблицы истинности:
Решение:
XYZ
5)
1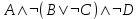
.Какое логическое выражение равносильно выражению:
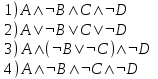
2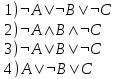
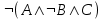. Какое логическое выражение равносильно выражению:
3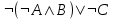
.Какое логическое выражение равносильно выражению:
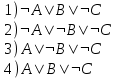
Решение:
Мы живем в таком мире, когда получаем много информации из непроверенных источников. Из рекламы, из никем не проверяемых книг, из средств массовой информации, от малознакомых людей. Если мы не хотим быть обманутыми, стоит научиться распознавать ложь.
Математическая логика и логика научного метода достаточно развились для того, чтобы сделать очередной шаг: рассмотреть возможность их применения не только в науке, но и в обычном общении.
Список используемой литературы
Как в классической, так и в интуиционистской логике «двойное отрицание» ¬¬� является следствием суждения �, то есть имеет место тавтология: �→¬¬�
Обратное утверждение ¬¬�→�и верно в классической логике (закон двойного отрицания), но не имеет места в интуиционистской. То есть отрицание отрицания искомого утверждения не может служить интуиционистским доказательством, в отличие от классической логики. Это различие двух логических систем обычно полагается главным.
Схематика
Мнемоническое правило для отрицания звучит так: на выходе будет
-
«1» тогда и только тогда, когда на входе «0», -
«0» тогда и только тогда, когда на входе «1».
Дизъюнкция
Дизъю́нкция (от лат. disjunctio — «разобщение»), логи́ческое сложе́ние, логи́ческое ИЛИ, включа́ющее ИЛИ; иногда просто ИЛИ — логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу».
Дизъюнкция может быть операцией как бинарной (имеющей два операнда), так и � -арной (имеющей � операндов) для произвольного �.
Запись может быть префиксной — знак операции стоит перед операндами (польская запись), инфиксной — знак операции стоит между операндами или постфиксной — знак операции стоит после операндов. При числе операндов более двух префиксная и постфиксная записи экономичнее.
Импликация
Имплика́ция (от лат. implicatio «связь; сплетение») — бинарная логическая связка, по своему применению приближенная к союзам «если…, то…».
Импликация записывается как посылка ⇒ следствие; применяются также стрелки другой формы и направленные в другую сторону, но всегда указывающие на следствие.
Суждение, выражаемое импликацией, выражается также следующими способами:
-
посылка является условием, достаточным для выполнения следствия: -
следствие является условием, необходимым для истинности посылки.
Импликация играет очень важную роль в умозаключениях. С её помощью формулируются определения различных понятий, теоремы, научные законы.
При учёте смыслового содержания высказываний импликация подразумевает причинную связь между посылкой и заключением.
Конъюнкция
Конъю́нкция (от лат. conjunctio — «союз, связь») — логическая операция, по смыслу максимально приближенная к союзу «и». Синонимы: логи́ческое «И», логи́ческое умноже́ние, иногда просто «И».
Конъюнкция может быть бинарной операцией (т. e. иметь два операнда), тернарной операцией (т. e. иметь три операнда), или n-арной операцией (т. e. иметь n операндов).
Эквиваленция
Логическая равнозначность или эквивале́нция (или эквивале́нтность) — это логическое выражение, которое является истинным тогда, когда оба простых логических выражения имеют одинаковую истинность. Двуместная логическая операция обычно обозначается символом ≡ или ↔.
| � | � | �≡� |
| | 0 | |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | |
Задаётся следующей таблицей истинности:
Таким образом, высказывание A ≡ B означает «A то же самое, что B», «A эквивалентно B», «A тогда и только тогда, когда B».
Не надо путать эквиваленцию — логическую операцию с логической эквивалентностью высказываний — бинарным отношением. Связь между ними следующая:
Логические выражения � и � эквивалентны в том и только в том случае, когда эквиваленция �⟺� истинна при всех значениях логических переменных.
Заключение
При исследовании данной темы было изучено большое количество теоретических источников, что способствовало систематизации знаний по этой теме. В заключительной части работы я решил применить полученные знания на практике. Тем самым я еще раз подтвердил выдвинутую гипотезу, что математическая логика активно применяется в наше время.
Практическая работа.
1)Установите, какие из следующих предложений являются логическими высказываниями, а какие — нет (объясните почему):
-
Солнце является спутником Земли; -
5+3?4; -
сегодня отличная погода; -
Санкт-Петербург расположен на Неве; -
Давайте слушать музыку Баха; -
первая космическая скорость равна 7.8 км/сек; -
железо — металл; -
Квадрат гипотенузы равен сумме квадратов катетов.
Решение:
| № высказывания | Логическое высказывание (имеет свойство быть истинным или ложным). | Предложения (не имеет свойство быть истинным или ложным). |
| 1 | + | |
| 2 | | + |
| 3 | + | |
| 4 | + | |
| 5 | | + |
| 6 | + | |
| 7 | + | |
| 8 | + | |
2)Укажите, какие из высказываний предыдущего задания истинны, какие — ложны, а какие относятся к числу тех, истинность которых трудно или невозможно установить.
Решение:
| № высказываний | Истинное | Ложное | Трудно или невозможно установить истинность |
| 1 | | + | |
| 3 | | | + |
| 4 | + | | |
| 6 | | + | |
| 7 | + | | |
| 8 | + | | |
3)Составьте таблицы истинности логических выражений:
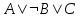
| A | B | C | 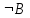 | F(A,B,C) |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| A | B | C | 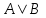 | 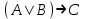 | F(A,B,C) |
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 |
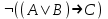
| A | B | C | 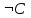 | 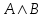 | 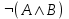 | F(A,B,C) |
| 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 |
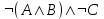
4)Составьте логическую функцию F (X, Y, Z) для заданной таблицы истинности:
| X | Y | Z | F |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Решение:
XYZ
5)
1
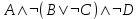.Какое логическое выражение равносильно выражению: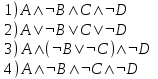 2
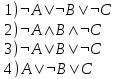
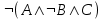. Какое логическое выражение равносильно выражению:3
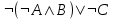.Какое логическое выражение равносильно выражению: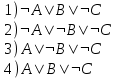 Решение:
| № выражения | Вариант ответа |
| 1 | 1 |
| 2 | 3 |
| 3 | 3 |
Мы живем в таком мире, когда получаем много информации из непроверенных источников. Из рекламы, из никем не проверяемых книг, из средств массовой информации, от малознакомых людей. Если мы не хотим быть обманутыми, стоит научиться распознавать ложь.
Математическая логика и логика научного метода достаточно развились для того, чтобы сделать очередной шаг: рассмотреть возможность их применения не только в науке, но и в обычном общении.
Список используемой литературы
-
Савин А.Н. «Энциклопедический словарь юного математика» М.: «Просвещение» 1985. -
Игошин В.И. «Задачи и упражнения по математической логике и теории алгоритмов». – 3-е изд., – М.: Издательский центр «Академия», 2007. -
Успенский В.А., Верещагин Н.К., Плиско В.Е. Вводный курс математической логики. 2-е изд. – М.: Физматлит, 2002. -
В.Ф. Пономарев Математическая логика. часть 1. Логика высказываний. Логика предикатов. Учебное пособие – Калининград: КГТУ, 2001 -
Игошин, Владимир Иванович. Задачи и упражнения по математической логике и теория алгоритмов :учебное пособие для вузов/В. И. Игошин.-4-е изд., стереотип.-М.:Академия,2008.-302с. -
Лихтарников, Леонид Моисеевич. Математическая логика :курс лекций : задачник-практикум и решения : учебное пособие для вузов/Л. М. Лихтарников, Т. Г. Сукачева.-СПб.:Лань,2008.-276 с.: -
Яглом И.М. Булева структура и ее модели. М.: Сов. радио, 1980. -
Шабунин Л.В. Математическая логика. Логика высказываний и логика предикатов. – Чебоксары: Изд-во Чуваш. ун-та, 2003. -
Судоплатов С.В., Овчинникова Е.В. Математическая логика и теория алгоритмов. – М.: ИНФРА-М, Новосибирск: Изд-во НГТУ, 2004. -
https://rstu.ru/metods/books/matlog2008.pdf