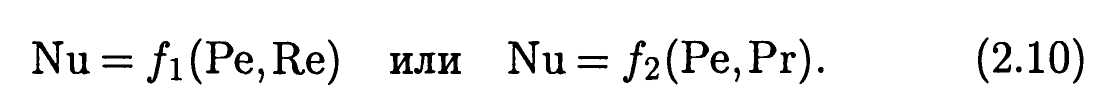ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 59
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
критериями подобия .
Объекты, для которых равны значения соответствующих критериев подобия, считают подобными. Например, любой треугольник однозначно определен длинами a, bи с его сторон, т.е n= 3, a k= 1. Поэтому, согласно П-теореме, множество подобных треугольников можно задать значениями = п — к = 2 критериев подобия. В качестве таких критериев можно выбрать безразмерные отношения длин сторон: b/а и с/а или любые два других независимых отношения. Так как углы треугольника однозначно связаны с отношениями сторон и являются безразмерными величинами, то множество подобных треугольников можно определить равенством двух соответствующих углов или равенством угла и отношения длин прилегающих к нему сторон. Все перечисленные варианты соответствуют известным признакам подобия треугольников.
= п — к = 2 критериев подобия. В качестве таких критериев можно выбрать безразмерные отношения длин сторон: b/а и с/а или любые два других независимых отношения. Так как углы треугольника однозначно связаны с отношениями сторон и являются безразмерными величинами, то множество подобных треугольников можно определить равенством двух соответствующих углов или равенством угла и отношения длин прилегающих к нему сторон. Все перечисленные варианты соответствуют известным признакам подобия треугольников.
Для успешного применения П-теоремы к построению моделей ТО необходимо располагать полным набором параметров, описывающих изучаемый объект, причем выбор этих параметров должен опираться на аргументированный качественный анализ тех свойств и особенностей ТО, влияние которых существенно в данном конкретном случае. Отметим, что такой анализ необходим при любом способе построения ММ, и проиллюстрируем это положение примерами.
Пример 2.1. Рассмотрим хорошо известную расчетную схему математического маятника (рис. 2.1) в виде материальной точки массой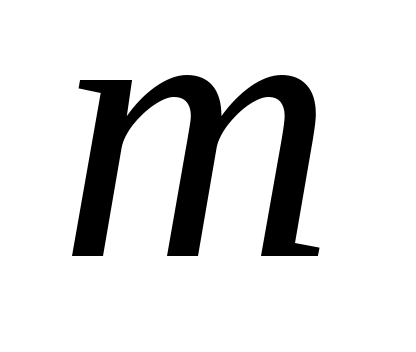 , подвешенной на невесомом стержне постоянной длины
, подвешенной на невесомом стержне постоянной длины 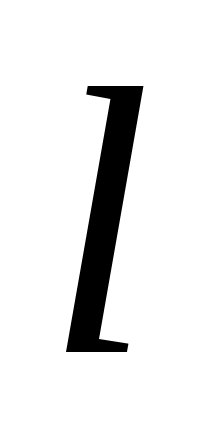 , который может свободно вращаться относительно горизонтальной оси, проходящей через точку О. Отклонение маятника на угол
, который может свободно вращаться относительно горизонтальной оси, проходящей через точку О. Отклонение маятника на угол  от его вертикального положения
от его вертикального положения
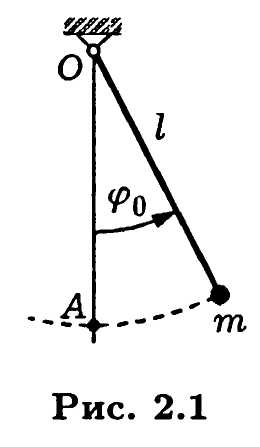
равновесия приведет к возрастанию потенци
альной энергии материальной точки на величину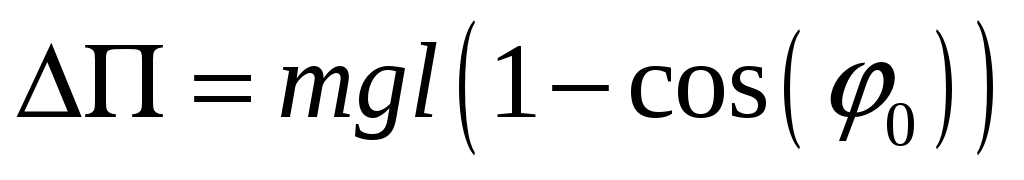 где
где 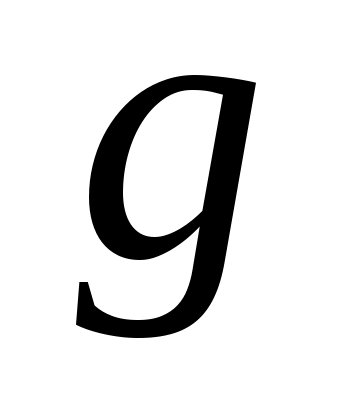 — ускорение свободного падения. Если после отклонения маятник начнет движение, то при отсутствии сопротивления он в силу закона сохранения энергии будет совершать незатухающие колебания относительно положения равновесия (точка А на рис. 2.1). При прохождении положения равновесия скорость vматериальной точки является наибольшей по абсолютной величине, поскольку в этом положении кинетическая энергия этой точки равна
— ускорение свободного падения. Если после отклонения маятник начнет движение, то при отсутствии сопротивления он в силу закона сохранения энергии будет совершать незатухающие колебания относительно положения равновесия (точка А на рис. 2.1). При прохождении положения равновесия скорость vматериальной точки является наибольшей по абсолютной величине, поскольку в этом положении кинетическая энергия этой точки равна 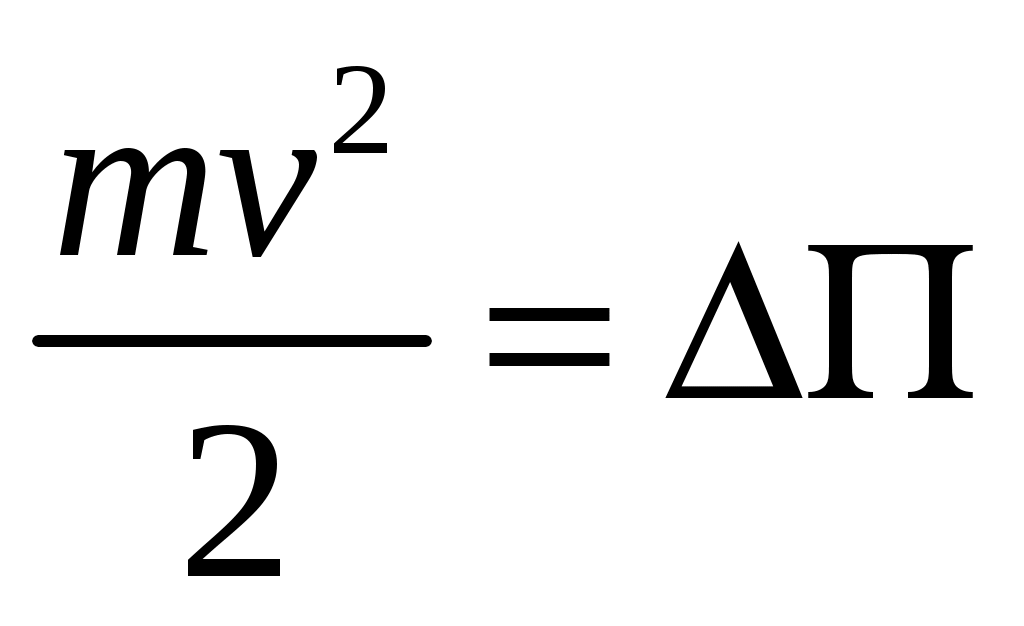 , так
, так
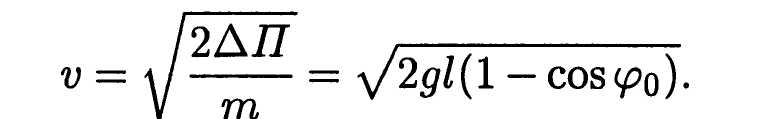
Пусть необходимо установить зависимость периода Т колебаний маятника (т.е. наименьшего промежутка времени, через который маятник возвращается в некоторое фиксированное положение, не совпадающее с положением равновесия) от параметров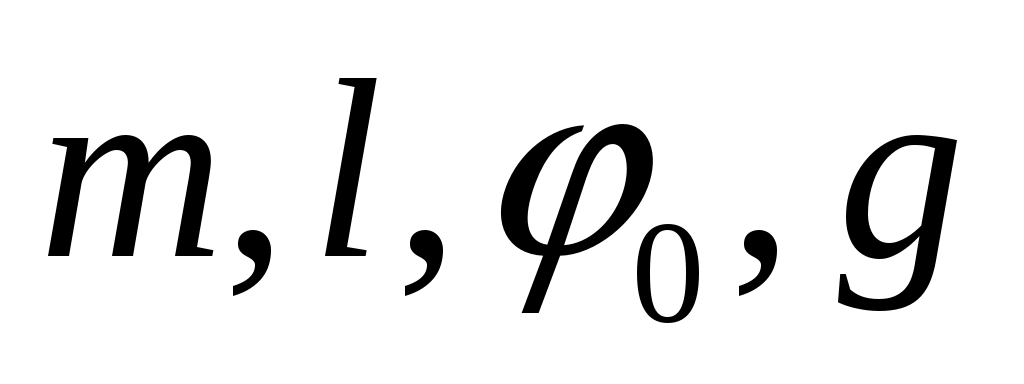 (параметр vследует исключить из рассмотрения, поскольку его удалось выразить через указанные выше параметры). Размерности [.] четырех указанных параметров и периода Т колебаний можно выразить через к = 3 независимые стандартные единицы измерения: [Т] = с, [т] = кг, [l]= мс, [
(параметр vследует исключить из рассмотрения, поскольку его удалось выразить через указанные выше параметры). Размерности [.] четырех указанных параметров и периода Т колебаний можно выразить через к = 3 независимые стандартные единицы измерения: [Т] = с, [т] = кг, [l]= мс, [ ] = 0 и [g] = м/с2. Поэтому в силу П-теоремы из п = 5 параметров можно составить
] = 0 и [g] = м/с2. Поэтому в силу П-теоремы из п = 5 параметров можно составить 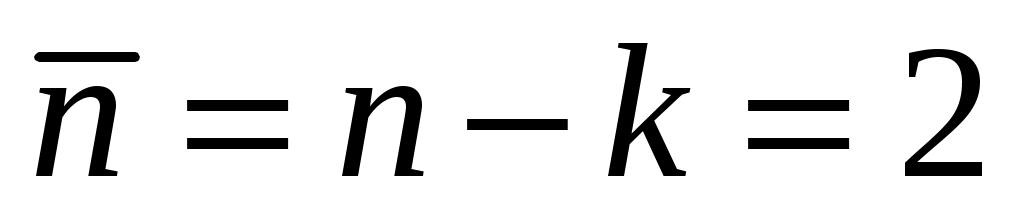 безразмерные комбинации, причем угол
безразмерные комбинации, причем угол  , будучи безразмерным, является одной из них. Во вторую безразмерную комбинацию не удается включить массу mматериальной точки, поскольку единица измерения массы (кг) входит лишь в размерность массы. Следовательно, величина
, будучи безразмерным, является одной из них. Во вторую безразмерную комбинацию не удается включить массу mматериальной точки, поскольку единица измерения массы (кг) входит лишь в размерность массы. Следовательно, величина
mне является аргументом искомой зависимости, что можно установить и при построении теоретической ММ рассматриваемого маятника (см. пример 5.12). После исключения параметра mимеем п = 4 и к = 2, т.е. снова п = 2, так что наряду с безразмерным параметром остальные
остальные
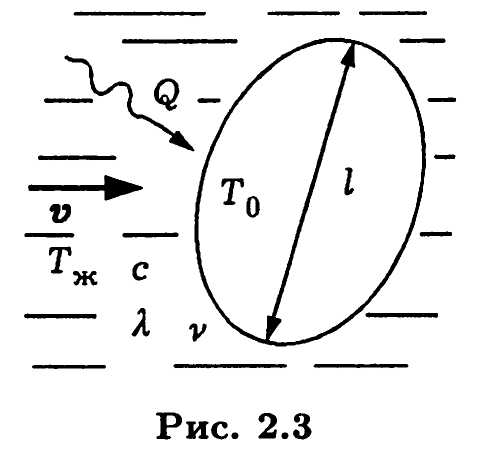
Пример 2.3. Пусть поток несжимаемой жидкости обтекает неподвижное твердое тело заданной формы, имеющее характерный размер и постоянную температуру То (рис. 2.3). Скорость vи температура Тж > То жидкости на большом (по сравнению с I) расстоянии от тела сохраняют постоянные значения. Необходимо при некотором фиксированном положении тела относительно направления вектора vскорости найти количество теплоты Q, передаваемое в единицу времени от жидкости к телу и называемое тепловым потоком.
и постоянную температуру То (рис. 2.3). Скорость vи температура Тж > То жидкости на большом (по сравнению с I) расстоянии от тела сохраняют постоянные значения. Необходимо при некотором фиксированном положении тела относительно направления вектора vскорости найти количество теплоты Q, передаваемое в единицу времени от жидкости к телу и называемое тепловым потоком.
Процесс передачи теплоты локализован у поверхности тела и зависит не только от перечисленных параметров, но и от объемной теплоемкости с и коэффициента теплопроводности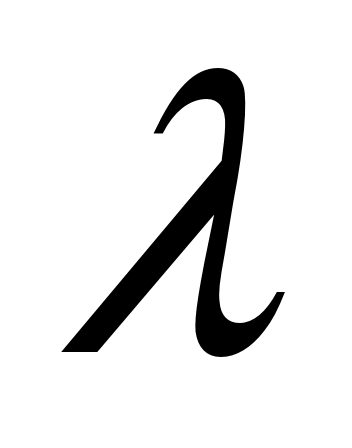 жидкости, поскольку эти параметры характеризуют способность жидкости подводить тепловую энергию и передавать ее поверхности тела. Подвод тепловой энергии к телу также зависит от распределения скорости жидкости у его поверхности. В случае идеальной (невязкой) жидкости оно однозначно определено фиксированным положением тела относительно вектора v, а для вязкой жидкости зависит и от соотношения между силами вязкости и инерции, характеризуемого коэффициентом вязкости
жидкости, поскольку эти параметры характеризуют способность жидкости подводить тепловую энергию и передавать ее поверхности тела. Подвод тепловой энергии к телу также зависит от распределения скорости жидкости у его поверхности. В случае идеальной (невязкой) жидкости оно однозначно определено фиксированным положением тела относительно вектора v, а для вязкой жидкости зависит и от соотношения между силами вязкости и инерции, характеризуемого коэффициентом вязкости 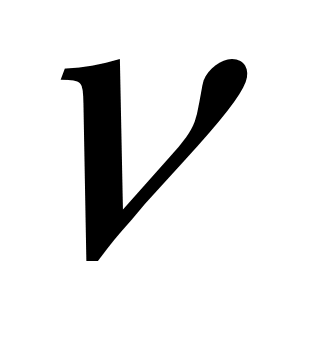
, называемым кинематическим и измеряемым в м2/с.
При сравнительно близких значениях Тж и То естественно предположить, что тепловой поток зависит не от каждой из этих температур, а от их разности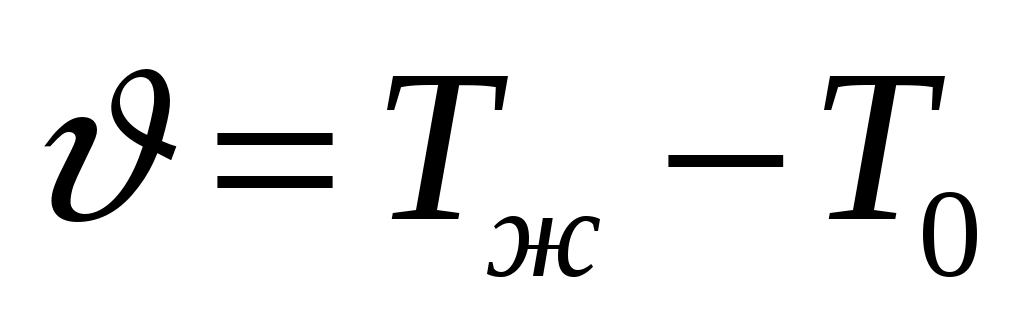 . Тогда в случае идеальной жидкости имеем п = 6 размерных параметров, размерности которых можно выразить через к = 4 независимые стандартные единицы измерения: [l] = м, [v] = м/с,
. Тогда в случае идеальной жидкости имеем п = 6 размерных параметров, размерности которых можно выразить через к = 4 независимые стандартные единицы измерения: [l] = м, [v] = м/с,
[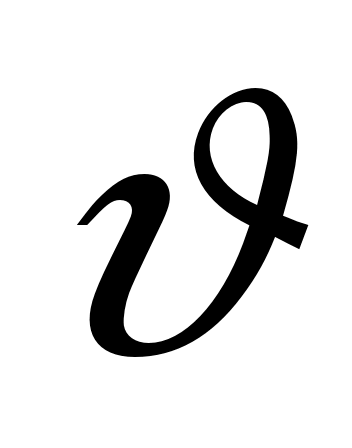 ] =K, [Q]=Дж/с=Вт=н
] =K, [Q]=Дж/с=Вт=н м/с, [c]=Дж/(м3К)=кг/(м
м/с, [c]=Дж/(м3К)=кг/(м с2
с2 К), [
К), [ ]=Вт/(м
]=Вт/(м К)=кг
К)=кг м/(с3К), где Дж (джоуль) и Вт (ватт) — единицы измерения энергии (работы) и мощности соответственно, а К (кельвин ) — единица измерения температуры в абсолютной шкале. В силу П-теоремы из этих параметров можно составить лишь п = п — к = 2 независимые безразмерные комбинации, например
м/(с3К), где Дж (джоуль) и Вт (ватт) — единицы измерения энергии (работы) и мощности соответственно, а К (кельвин ) — единица измерения температуры в абсолютной шкале. В силу П-теоремы из этих параметров можно составить лишь п = п — к = 2 независимые безразмерные комбинации, например 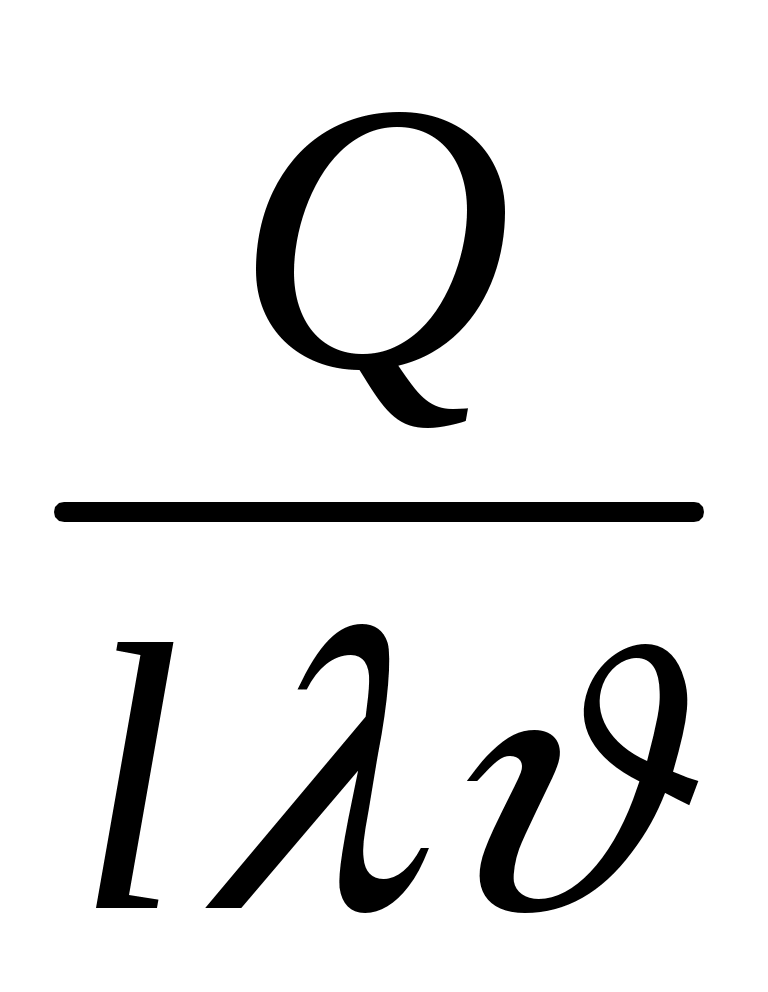 и
и 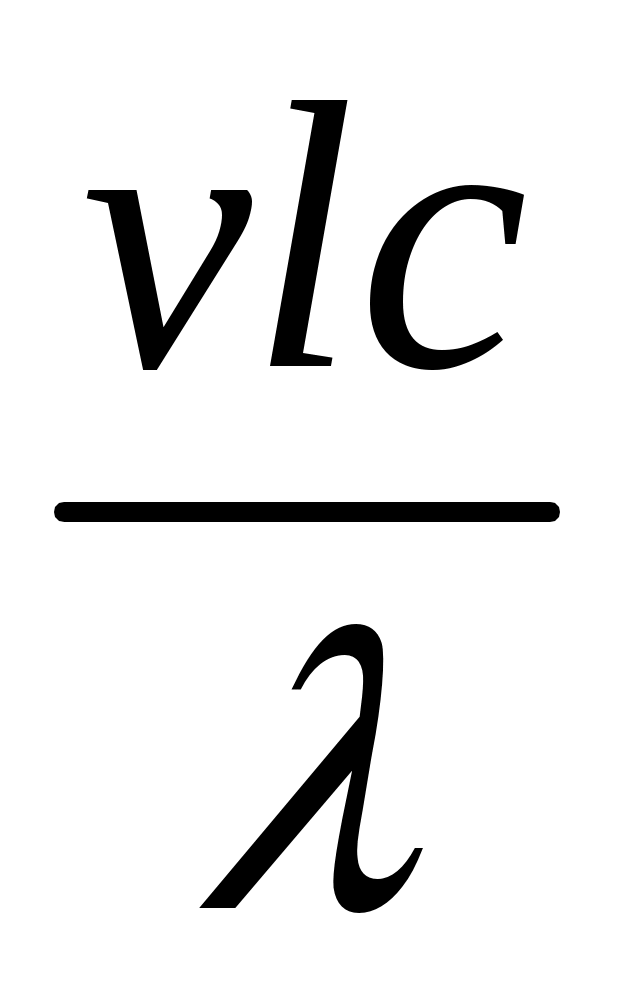 . В итоге приходим к функциональной зависимости
. В итоге приходим к функциональной зависимости

установленной в 1915 г. Дж.У. Стреттом .
Отношение q = Q/Sназывают усредненной по площади Sповерхности тела плотностью теплового потока и измеряют в Вт/м2. Так как для геометрически подобных тел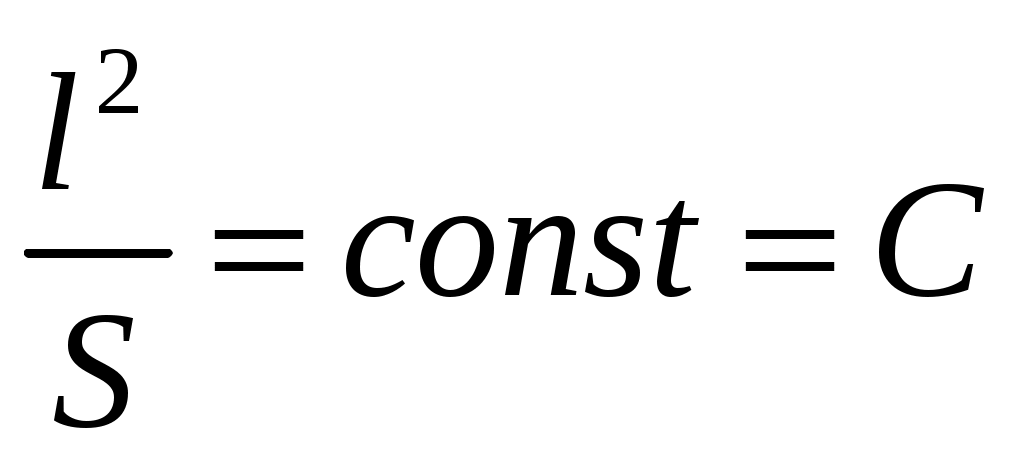
, то (2.7) можно представить в виде
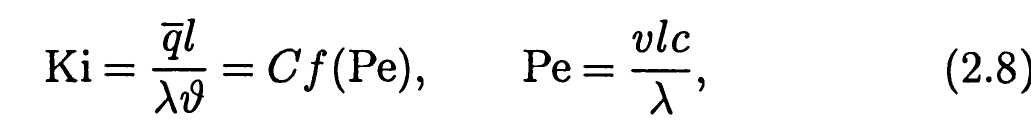
где Ki — тепловой критерий Кирпичева и Ре — критерий Пекле. Интенсивность теплообмена на поверхности тела обычно характеризуют усредненным коэффициентом теплоотдачи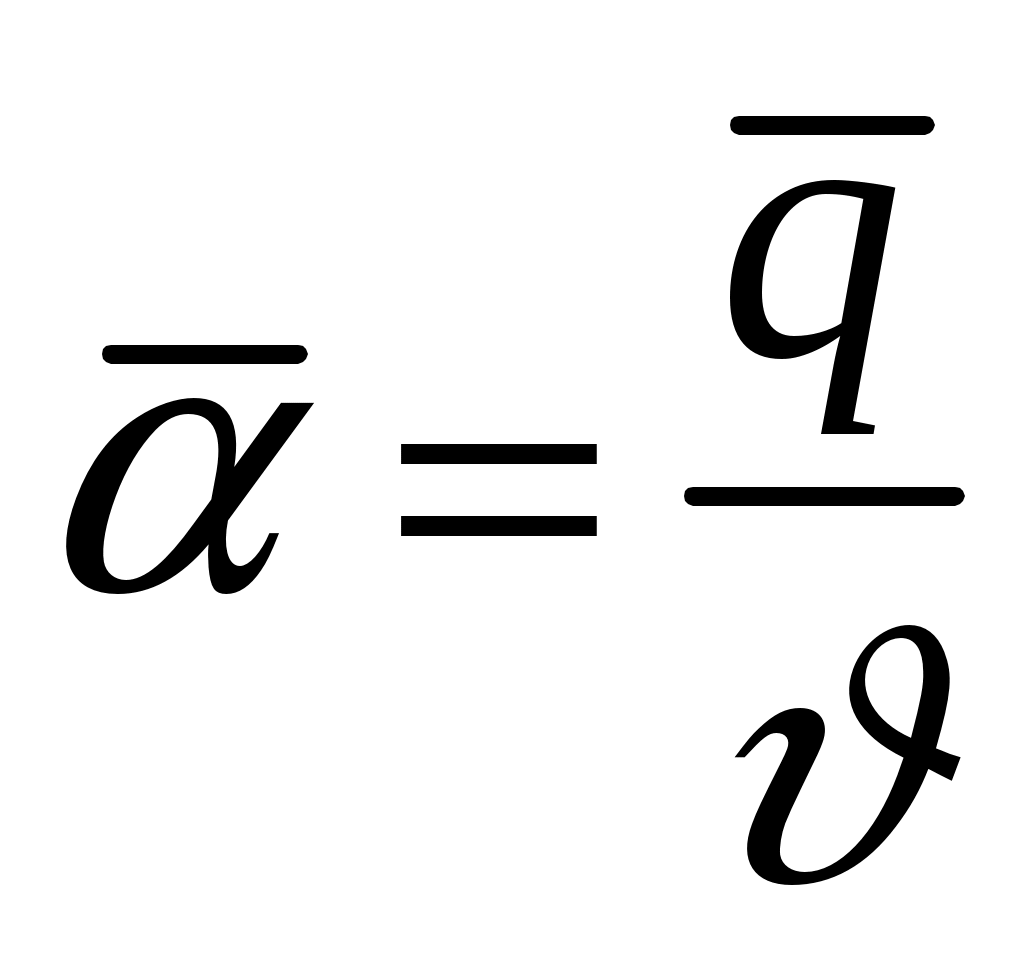 — , измеряемым в Вт/(м2К). Тогда вместо (2.8) получим
— , измеряемым в Вт/(м2К). Тогда вместо (2.8) получим
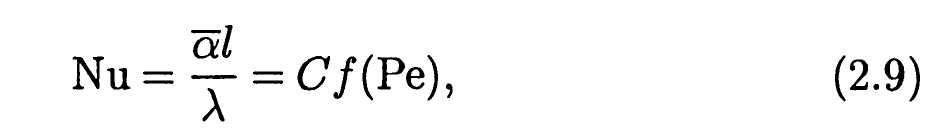
где Nu — критерий (число) Нуссельта . Вид функции в (2.7)-(2.9) нельзя установить в рамках теории размерностей и его приходится определять путем обработки результатов экспериментов, хотя в некоторых простых случаях удается построить и теоретические ММ процесса теплообмена.
в (2.7)-(2.9) нельзя установить в рамках теории размерностей и его приходится определять путем обработки результатов экспериментов, хотя в некоторых простых случаях удается построить и теоретические ММ процесса теплообмена.
В случае вязкой жидкости имеем п = 7 размерных параметров, размерности которых по-прежнему можно выразить через к = 4 независимые единицы измерения, т.е. число независмых безразмерных комбинаций равно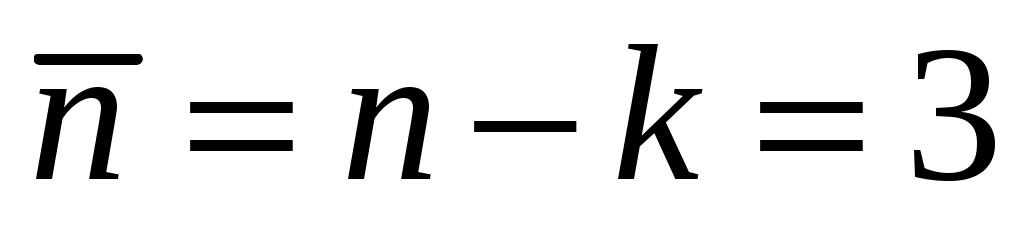 . К рассмотренным выше следует добавить любую безразмерную комбинацию, включающую новый параметр и. Эту комбинацию можно выбрать, например, в виде
. К рассмотренным выше следует добавить любую безразмерную комбинацию, включающую новый параметр и. Эту комбинацию можно выбрать, например, в виде 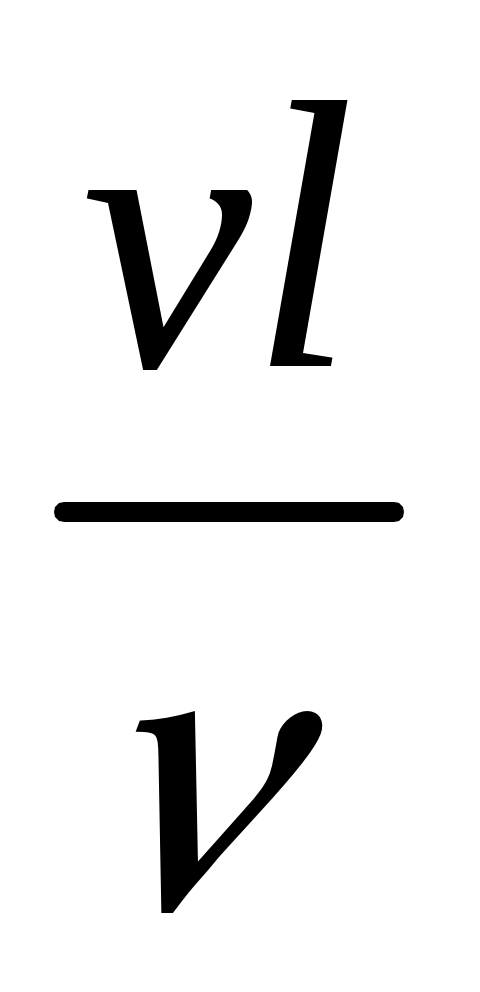 или
или 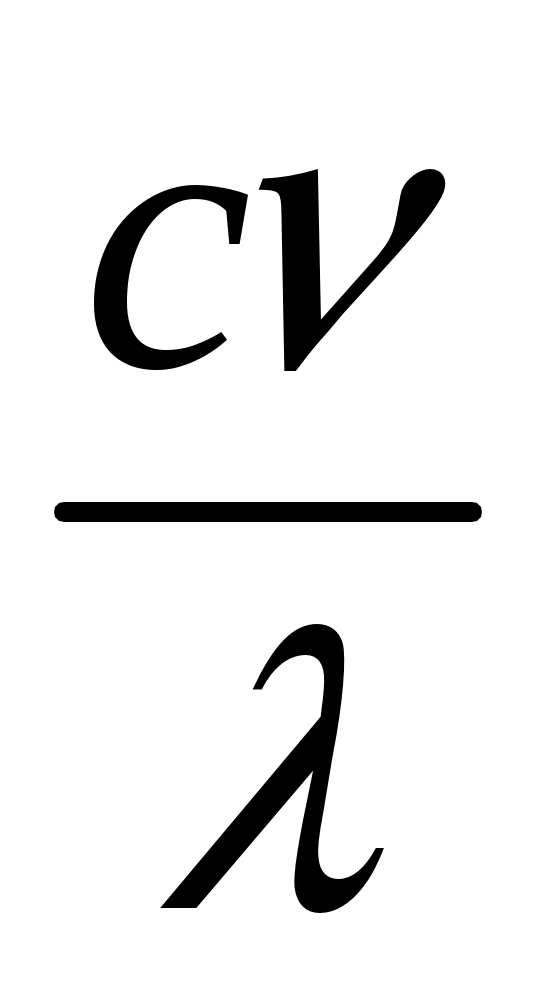 . В первом случае ее называют критерием (числом) Рейнолъдса и обозначают Re =
. В первом случае ее называют критерием (числом) Рейнолъдса и обозначают Re = 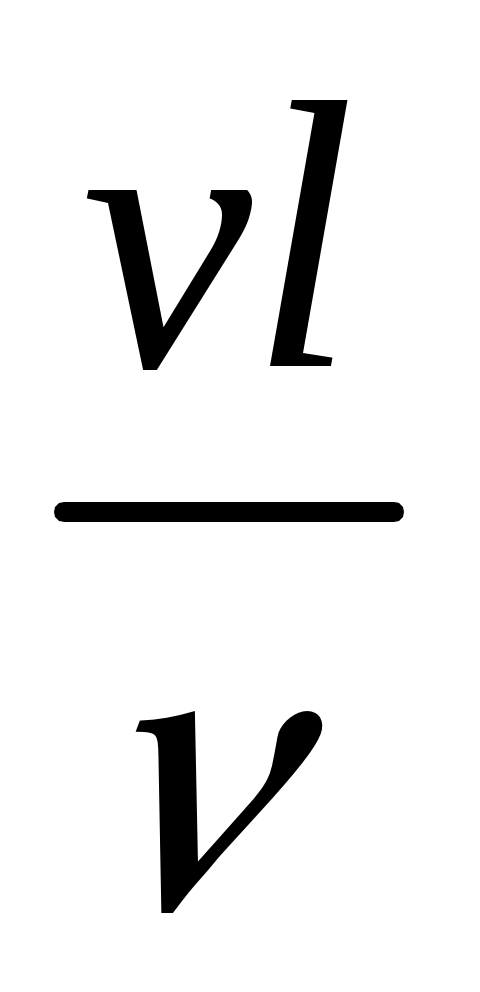 , а во втором — критерием (числом)Прандтля и обозначают Рг =
, а во втором — критерием (числом)Прандтля и обозначают Рг = 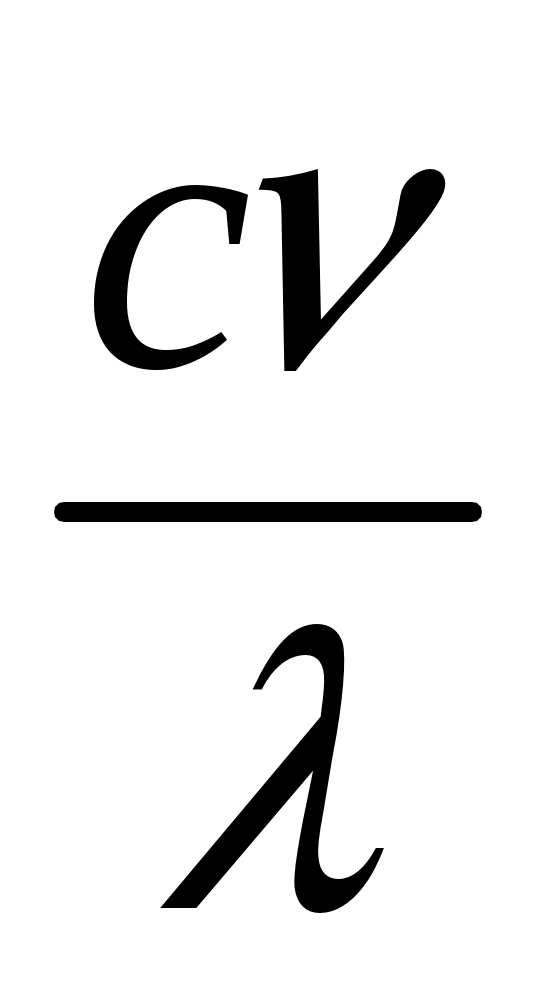 . Критерий Прандтля характеризует только свойства жидкости, а критерий Рейнольдса — соотношение между инерционными силами и силами вязкого трения. В итоге вместо (2.9) получим
. Критерий Прандтля характеризует только свойства жидкости, а критерий Рейнольдса — соотношение между инерционными силами и силами вязкого трения. В итоге вместо (2.9) получим
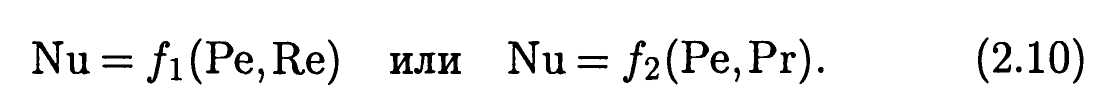
Объекты, для которых равны значения соответствующих критериев подобия, считают подобными. Например, любой треугольник однозначно определен длинами a, bи с его сторон, т.е n= 3, a k= 1. Поэтому, согласно П-теореме, множество подобных треугольников можно задать значениями
Для успешного применения П-теоремы к построению моделей ТО необходимо располагать полным набором параметров, описывающих изучаемый объект, причем выбор этих параметров должен опираться на аргументированный качественный анализ тех свойств и особенностей ТО, влияние которых существенно в данном конкретном случае. Отметим, что такой анализ необходим при любом способе построения ММ, и проиллюстрируем это положение примерами.
Пример 2.1. Рассмотрим хорошо известную расчетную схему математического маятника (рис. 2.1) в виде материальной точки массой

равновесия приведет к возрастанию потенци
альной энергии материальной точки на величину
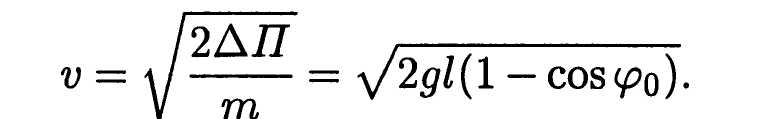
Пусть необходимо установить зависимость периода Т колебаний маятника (т.е. наименьшего промежутка времени, через который маятник возвращается в некоторое фиксированное положение, не совпадающее с положением равновесия) от параметров
mне является аргументом искомой зависимости, что можно установить и при построении теоретической ММ рассматриваемого маятника (см. пример 5.12). После исключения параметра mимеем п = 4 и к = 2, т.е. снова п = 2, так что наряду с безразмерным параметром
Пример 2.3. Пусть поток несжимаемой жидкости обтекает неподвижное твердое тело заданной формы, имеющее характерный размер

Процесс передачи теплоты локализован у поверхности тела и зависит не только от перечисленных параметров, но и от объемной теплоемкости с и коэффициента теплопроводности
, называемым кинематическим и измеряемым в м2/с.
При сравнительно близких значениях Тж и То естественно предположить, что тепловой поток зависит не от каждой из этих температур, а от их разности
[

установленной в 1915 г. Дж.У. Стреттом .
Отношение q = Q/Sназывают усредненной по площади Sповерхности тела плотностью теплового потока и измеряют в Вт/м2. Так как для геометрически подобных тел
, то (2.7) можно представить в виде
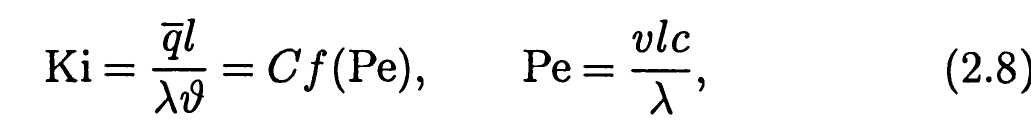
где Ki — тепловой критерий Кирпичева и Ре — критерий Пекле. Интенсивность теплообмена на поверхности тела обычно характеризуют усредненным коэффициентом теплоотдачи
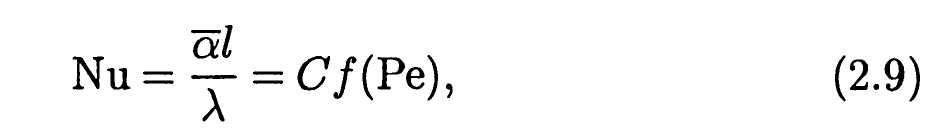
где Nu — критерий (число) Нуссельта . Вид функции
В случае вязкой жидкости имеем п = 7 размерных параметров, размерности которых по-прежнему можно выразить через к = 4 независимые единицы измерения, т.е. число независмых безразмерных комбинаций равно