ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 58
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ММ. Например, среди структурных математических моделей ТО к более высокому уровню иерархии относят топологические математические модели, а к более низкому уровню, характеризующемуся большей детализацией ТО, — геометрические математические модели.
Среди функциональных математических моделей иерархические уровни отражают степень детализации описания процессов, протекающих в ТО, его блоках или элементах. С этой точки зрения обычно выделяют три основных уровня: микро-, макро- и метауровень.
Математические модели микроуровня описывают процессы в системах с распределенными параметрами (в континуальных системах), а математические модели макроуровня — в системах с сосредоточенными параметрами (в дискретных системах). В первых из них фазовые переменные могут зависеть как от времени, так и от пространственных координат, а во вторых — только от времени.
Если в ММ макроуровня число фазовых переменных имеет порядок 104-105, то количественный анализ такой ММ становится громоздким и требует значительных затрат вычислительных ресурсов. Кроме того, при столь большом числе фазовых переменных трудно выделить существенные характеристики ТО и особенности его поведения. В таком случае путем объединения и укрупнения элементов сложного ТО стремятся уменьшить число фазовых переменных за счет исключения из рассмотрения внутренних параметров элементов, ограничиваясь лишь описанием взаимных связей между укрупненными элементами. Такой подход характерен для математических моделей метауровня.
ММ метауровня обычно относят к высшему уровню иерархии, ММ макроуровня — к среднему, а ММ микроуровня — к низшему. Наиболее распространенной формой представления динамической (эволюционной) математической модели микроуровня является формулировка краевой задачи для дифференциальных уравнений математической физики [XII]. Такая формулировка включает дифференциальные уравнения с частными производными и краевые условия. В свою очередь, краевые условия со
держат начальные условия — распределения искомых фазовых переменных в некоторый момент времени, принимаемый за начальный, в пространственной области, конфигурация которой соответствует рассматриваемому ТО или его элементу, — и граничные условия на границах этой области. При представлении ММ целесообразно использовать безразмерные переменные (независимые и искомые) и коэффициенты уравнений, сократив число параметров, характеризующих рассматриваемый ТО (см. Д.2.2).
ММ микроуровня называют одномерной, двумерной или трехмерной, если искомые фазовые переменные зависят от одной, двух или трех пространственных координат соответственно. Два последних типа ММ объединяют в многомерные математические модели микроуровнл. Одномерная ММ микроуровня, фазовые переменные в которой не зависят от времени, имеет представление в виде системы ОДУ с заданными граничными условиями (в простейшем случае одного фазового переменного такая ММ включает лишь одно ОДУ и граничные условия).
Поскольку краевой задаче, содержащей дифференциальные уравнения с частными производными и краевые условия, можно поставить в соответствие интегральную формулировку , то и ММ микроуровня также может быть представлена в интегральной форме. При определенных условиях интегральную форму краевой задачи удается привести к вариационной формулировке в виде функционала , который допустимо рассматривать на некотором множестве функций, содержащем искомую функцию. В этом случае говорят о вариационной форме модели микроуровня. Искомая функция обращает в нуль вариацию функционала, т.е. является его стационарной точкой.
Построение функционала и соответствующей ему вариационной формы модели микроуровня обычно основано на некотором содержательном с физической точки зрения вариационном принципе механики или электродинамики сплошной среды (например, на принципе минимума потенциальной энергии континуальной системы в положении равновесия или на принципе минимума времени прохождения светового луча между двумя точками оптически неоднородной среды). В этом случае стаци
онарная точка функционала соответствует его экстремальному (в частности, минимальному) значению на допустимом множестве функций. Такая форма модели микроуровня, называемая экстремальной вариационной, позволяет, сравнивая значения функционала на любых двух функциях из допустимого множества, оценивать в интегральном смысле близость этих функций к искомой. Это свойство экстремальной вариационной формы модели важно при качественном анализе ММ и при сравнении различных приближенных решений соответствующей краевой задачи*.
При выполнении некоторых ограничений можно построить двойственную вариационную форму модели микроуровня, включающую пару функционалов, достигающих в одной и той же стационарной точке равных между собой альтернативных экстремальных значений (минимума и максимума) . Такая форма ММ дает возможность по разности значений этих Функционалов, вычисленных на некоторой функции из допустимого множества, количественно оценить погрешность, возникающую при выборе этой функции в качестве искомой.
Основной формой динамической (эволюционной) ММ макроуровня являются ОДУ или их системы вместе с заданными начальными условиями. Независимым переменным в таких ММ будет время, а искомыми — фазовые переменные, характеризующие состояние ТО (например, перемещения, скорости и ускорения элементов механических устройств, а также приложенные к этим элементам силы и моменты; давление и расход жидкости или газа в трубопроводе; напряжения и силы тока в электрических цепях и т.п.). В некоторых случаях ММ макроуровня удается представить в интегральной форме, используя принцип Гамильтона — Остроградского или экстремальный вариационный принцип Гамильтона.
Если эволюцию ТО определяет его состояние не только в текущий момент времени t, но и в некоторый предшествующий момент t — τ, то ММ макроуровня включает ОДУ вида
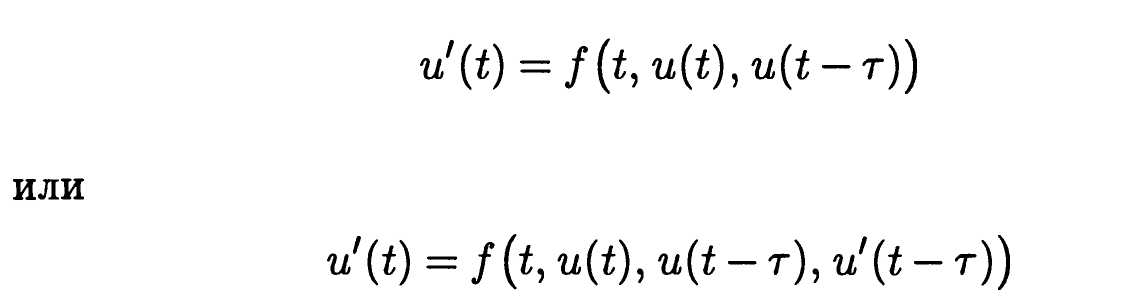
относительно искомой функции u(t). Такие ОДУ называют уравнениями запаздывающего и нейтрального типа соответ
ственно и относят к дифференциально-функциональным уравнениям* (ДФУ) (или дифференциальным уравнениям с отклоняющимся аргументом). Наиболее широко ДФУ и их системы представлены в ММ систем автоматического управления и регулирования. Кроме того, ДФУ находят применение в моделях биологических и экономических процессов.
Запаздывающая реакция ТО на изменение своего состояния может определяться более чем одним интервалом времени т. Тогда ДФУ будет включать не одно, а несколько дискретных запаздываний. В более общем случае запаздывание может быть непрерывным во времени, что приводит, например, для линейной математической модели к интегро-дифференциальному уравнению (ИДУ) вида
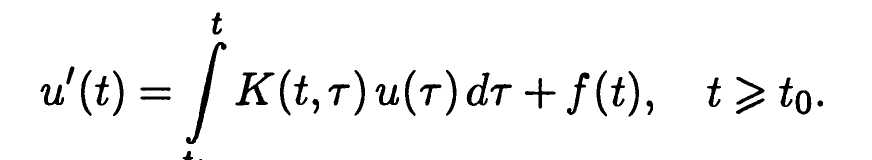
Заданную функцию K(t,r) называют ядром этого ИДУ, а о рассматриваемом ТО говорят, что он обладает памятью, поскольку его эволюция зависит от всей предыстории изменения состояний ТО.
В статическую математическую модель макроуровня не входит время. Поэтому она включает лишь конечное (в общем случае нелинейное) уравнение или систему таких уравнений (в частности, систему линейных алгебраических уравнений — СЛАУ). Такой же вид имеют квазистатическая, стационарная и квазистационарная математические модели макроуровня.
Если для рассматриваемого ТО удается выделить поддающееся количественной характеристике некоторое важное свойство или сочетание таких свойств (надежность, долговечность, массу, стоимость, какой-либо из определяющих качество ТО выходных параметров) и установить их связь с фазовыми переменными при помощи действительной функции, то можно говорить об оптимизации ТО по критерию, выражаемому этой функцией. Ее называют целевой функцией [XIV], поскольку ее значения характеризуют меру (или степень) достижения определенной цели совершенствования ТО в соответствии с выбранным критерием.
Вследствие ограниченности располагаемых ресурсов в реальной ситуации имеют смысл лишь те экстремальные значения целевой функции, которые достигаются в области возможно
го изменения фазовых переменных ТО, обычно ограниченной системой неравенств. Эти неравенства вместе с целевой функцией и статической ММ ТО в виде конечного нелинейного Уравнения или систем таких уравнений входят в математическую формулировку задачи оптимизации ТО по выбранномукритерию, называемой (в общем случае) задачей нелинейного программирования [XIV]. В частном случае линейной математической модели ТО в виде СЛАУ, линейных целевой функции и неравенств говорят о задаче линейного программирования. К таким задачам обычно приходят при рассмотрении проблем технико-экономического содержания. Задачу оптимизации ТО, описываемого динамической (эволюционной) ММ макроуровня, относят к классу задач оптимального управления [XV].
Для ММ метауровня характерны те же типы уравнений, что и для ММ макроуровня, но эти уравнения включают фазовые переменные, описывающие состояние укрупненных элементов сложных ТО. Если определен закон непрерывного перехода ТО из одного состояния в другое, то для анализа ММ метауровня часто используют аппарат передаточных функций*, а при рассмотрении состояний ТО в дискретные моменты времени ОДУ и их системы переходят в разностные уравнения относительно значений фазовых переменных в эти моменты времени. В случае дискретного множества состояний ТО применяют также аппарат математической логики и конечных автоматов.
Среди функциональных математических моделей иерархические уровни отражают степень детализации описания процессов, протекающих в ТО, его блоках или элементах. С этой точки зрения обычно выделяют три основных уровня: микро-, макро- и метауровень.
Математические модели микроуровня описывают процессы в системах с распределенными параметрами (в континуальных системах), а математические модели макроуровня — в системах с сосредоточенными параметрами (в дискретных системах). В первых из них фазовые переменные могут зависеть как от времени, так и от пространственных координат, а во вторых — только от времени.
Если в ММ макроуровня число фазовых переменных имеет порядок 104-105, то количественный анализ такой ММ становится громоздким и требует значительных затрат вычислительных ресурсов. Кроме того, при столь большом числе фазовых переменных трудно выделить существенные характеристики ТО и особенности его поведения. В таком случае путем объединения и укрупнения элементов сложного ТО стремятся уменьшить число фазовых переменных за счет исключения из рассмотрения внутренних параметров элементов, ограничиваясь лишь описанием взаимных связей между укрупненными элементами. Такой подход характерен для математических моделей метауровня.
ММ метауровня обычно относят к высшему уровню иерархии, ММ макроуровня — к среднему, а ММ микроуровня — к низшему. Наиболее распространенной формой представления динамической (эволюционной) математической модели микроуровня является формулировка краевой задачи для дифференциальных уравнений математической физики [XII]. Такая формулировка включает дифференциальные уравнения с частными производными и краевые условия. В свою очередь, краевые условия со
держат начальные условия — распределения искомых фазовых переменных в некоторый момент времени, принимаемый за начальный, в пространственной области, конфигурация которой соответствует рассматриваемому ТО или его элементу, — и граничные условия на границах этой области. При представлении ММ целесообразно использовать безразмерные переменные (независимые и искомые) и коэффициенты уравнений, сократив число параметров, характеризующих рассматриваемый ТО (см. Д.2.2).
ММ микроуровня называют одномерной, двумерной или трехмерной, если искомые фазовые переменные зависят от одной, двух или трех пространственных координат соответственно. Два последних типа ММ объединяют в многомерные математические модели микроуровнл. Одномерная ММ микроуровня, фазовые переменные в которой не зависят от времени, имеет представление в виде системы ОДУ с заданными граничными условиями (в простейшем случае одного фазового переменного такая ММ включает лишь одно ОДУ и граничные условия).
Поскольку краевой задаче, содержащей дифференциальные уравнения с частными производными и краевые условия, можно поставить в соответствие интегральную формулировку , то и ММ микроуровня также может быть представлена в интегральной форме. При определенных условиях интегральную форму краевой задачи удается привести к вариационной формулировке в виде функционала , который допустимо рассматривать на некотором множестве функций, содержащем искомую функцию. В этом случае говорят о вариационной форме модели микроуровня. Искомая функция обращает в нуль вариацию функционала, т.е. является его стационарной точкой.
Построение функционала и соответствующей ему вариационной формы модели микроуровня обычно основано на некотором содержательном с физической точки зрения вариационном принципе механики или электродинамики сплошной среды (например, на принципе минимума потенциальной энергии континуальной системы в положении равновесия или на принципе минимума времени прохождения светового луча между двумя точками оптически неоднородной среды). В этом случае стаци
онарная точка функционала соответствует его экстремальному (в частности, минимальному) значению на допустимом множестве функций. Такая форма модели микроуровня, называемая экстремальной вариационной, позволяет, сравнивая значения функционала на любых двух функциях из допустимого множества, оценивать в интегральном смысле близость этих функций к искомой. Это свойство экстремальной вариационной формы модели важно при качественном анализе ММ и при сравнении различных приближенных решений соответствующей краевой задачи*.
При выполнении некоторых ограничений можно построить двойственную вариационную форму модели микроуровня, включающую пару функционалов, достигающих в одной и той же стационарной точке равных между собой альтернативных экстремальных значений (минимума и максимума) . Такая форма ММ дает возможность по разности значений этих Функционалов, вычисленных на некоторой функции из допустимого множества, количественно оценить погрешность, возникающую при выборе этой функции в качестве искомой.
Основной формой динамической (эволюционной) ММ макроуровня являются ОДУ или их системы вместе с заданными начальными условиями. Независимым переменным в таких ММ будет время, а искомыми — фазовые переменные, характеризующие состояние ТО (например, перемещения, скорости и ускорения элементов механических устройств, а также приложенные к этим элементам силы и моменты; давление и расход жидкости или газа в трубопроводе; напряжения и силы тока в электрических цепях и т.п.). В некоторых случаях ММ макроуровня удается представить в интегральной форме, используя принцип Гамильтона — Остроградского или экстремальный вариационный принцип Гамильтона.
Если эволюцию ТО определяет его состояние не только в текущий момент времени t, но и в некоторый предшествующий момент t — τ, то ММ макроуровня включает ОДУ вида
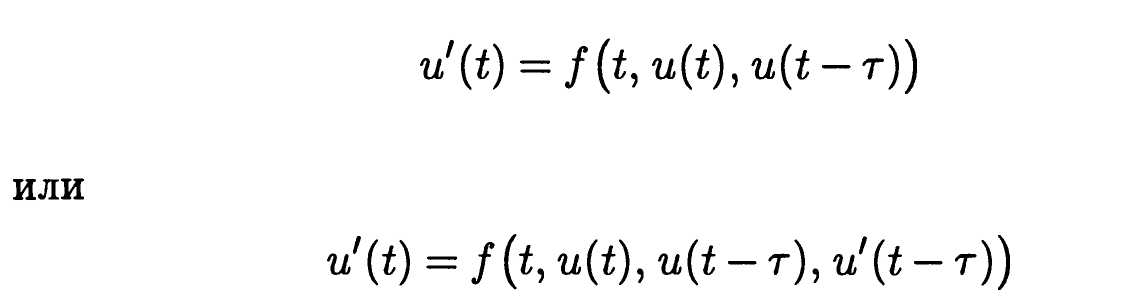
относительно искомой функции u(t). Такие ОДУ называют уравнениями запаздывающего и нейтрального типа соответ
ственно и относят к дифференциально-функциональным уравнениям* (ДФУ) (или дифференциальным уравнениям с отклоняющимся аргументом). Наиболее широко ДФУ и их системы представлены в ММ систем автоматического управления и регулирования. Кроме того, ДФУ находят применение в моделях биологических и экономических процессов.
Запаздывающая реакция ТО на изменение своего состояния может определяться более чем одним интервалом времени т. Тогда ДФУ будет включать не одно, а несколько дискретных запаздываний. В более общем случае запаздывание может быть непрерывным во времени, что приводит, например, для линейной математической модели к интегро-дифференциальному уравнению (ИДУ) вида
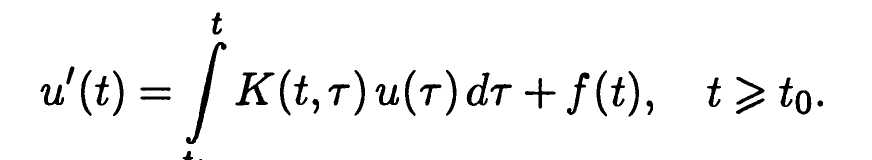
Заданную функцию K(t,r) называют ядром этого ИДУ, а о рассматриваемом ТО говорят, что он обладает памятью, поскольку его эволюция зависит от всей предыстории изменения состояний ТО.
В статическую математическую модель макроуровня не входит время. Поэтому она включает лишь конечное (в общем случае нелинейное) уравнение или систему таких уравнений (в частности, систему линейных алгебраических уравнений — СЛАУ). Такой же вид имеют квазистатическая, стационарная и квазистационарная математические модели макроуровня.
Если для рассматриваемого ТО удается выделить поддающееся количественной характеристике некоторое важное свойство или сочетание таких свойств (надежность, долговечность, массу, стоимость, какой-либо из определяющих качество ТО выходных параметров) и установить их связь с фазовыми переменными при помощи действительной функции, то можно говорить об оптимизации ТО по критерию, выражаемому этой функцией. Ее называют целевой функцией [XIV], поскольку ее значения характеризуют меру (или степень) достижения определенной цели совершенствования ТО в соответствии с выбранным критерием.
Вследствие ограниченности располагаемых ресурсов в реальной ситуации имеют смысл лишь те экстремальные значения целевой функции, которые достигаются в области возможно
го изменения фазовых переменных ТО, обычно ограниченной системой неравенств. Эти неравенства вместе с целевой функцией и статической ММ ТО в виде конечного нелинейного Уравнения или систем таких уравнений входят в математическую формулировку задачи оптимизации ТО по выбранномукритерию, называемой (в общем случае) задачей нелинейного программирования [XIV]. В частном случае линейной математической модели ТО в виде СЛАУ, линейных целевой функции и неравенств говорят о задаче линейного программирования. К таким задачам обычно приходят при рассмотрении проблем технико-экономического содержания. Задачу оптимизации ТО, описываемого динамической (эволюционной) ММ макроуровня, относят к классу задач оптимального управления [XV].
Для ММ метауровня характерны те же типы уравнений, что и для ММ макроуровня, но эти уравнения включают фазовые переменные, описывающие состояние укрупненных элементов сложных ТО. Если определен закон непрерывного перехода ТО из одного состояния в другое, то для анализа ММ метауровня часто используют аппарат передаточных функций*, а при рассмотрении состояний ТО в дискретные моменты времени ОДУ и их системы переходят в разностные уравнения относительно значений фазовых переменных в эти моменты времени. В случае дискретного множества состояний ТО применяют также аппарат математической логики и конечных автоматов.